

CN 11-1911/B
主办:中国心理学会
中国科学院心理研究所
出版:科学出版社


心理学报 ›› 2022, Vol. 54 ›› Issue (4): 426-440.doi: 10.3724/SP.J.1041.2022.00426 cstr: 32110.14.2022.00426
• 研究报告 • 上一篇
收稿日期:2021-06-10
发布日期:2022-02-21
出版日期:2022-04-25
通讯作者:
郭磊, E-mail: happygl1229@swu.edu.cn基金资助:
SONG Zhilin1, GUO Lei1,2( ), ZHENG Tianpeng3
), ZHENG Tianpeng3
Received:2021-06-10
Online:2022-02-21
Published:2022-04-25
摘要:
数据缺失在测验中经常发生, 认知诊断评估也不例外, 数据缺失会导致诊断结果的偏差。首先, 通过模拟研究在多种实验条件下比较了常用的缺失数据处理方法。结果表明:(1)缺失数据导致估计精确性下降, 随着人数与题目数量减少、缺失率增大、题目质量降低, 所有方法的PCCR均下降, Bias绝对值和RMSE均上升。(2)估计题目参数时, EM法表现最好, 其次是MI, FIML和ZR法表现不稳定。(3)估计被试知识状态时, EM和FIML表现最好, MI和ZR表现不稳定。其次, 在PISA2015实证数据中进一步探索了不同方法的表现。综合模拟和实证研究结果, 推荐选用EM或FIML法进行缺失数据处理。
中图分类号:
宋枝璘, 郭磊, 郑天鹏. (2022). 认知诊断缺失数据处理方法的比较:零替换、多重插补与极大似然估计法. 心理学报, 54(4), 426-440.
SONG Zhilin, GUO Lei, ZHENG Tianpeng. (2022). Comparison of missing data handling methods in cognitive diagnosis: Zero replacement, multiple imputation and maximum likelihood estimation. Acta Psychologica Sinica, 54(4), 426-440.
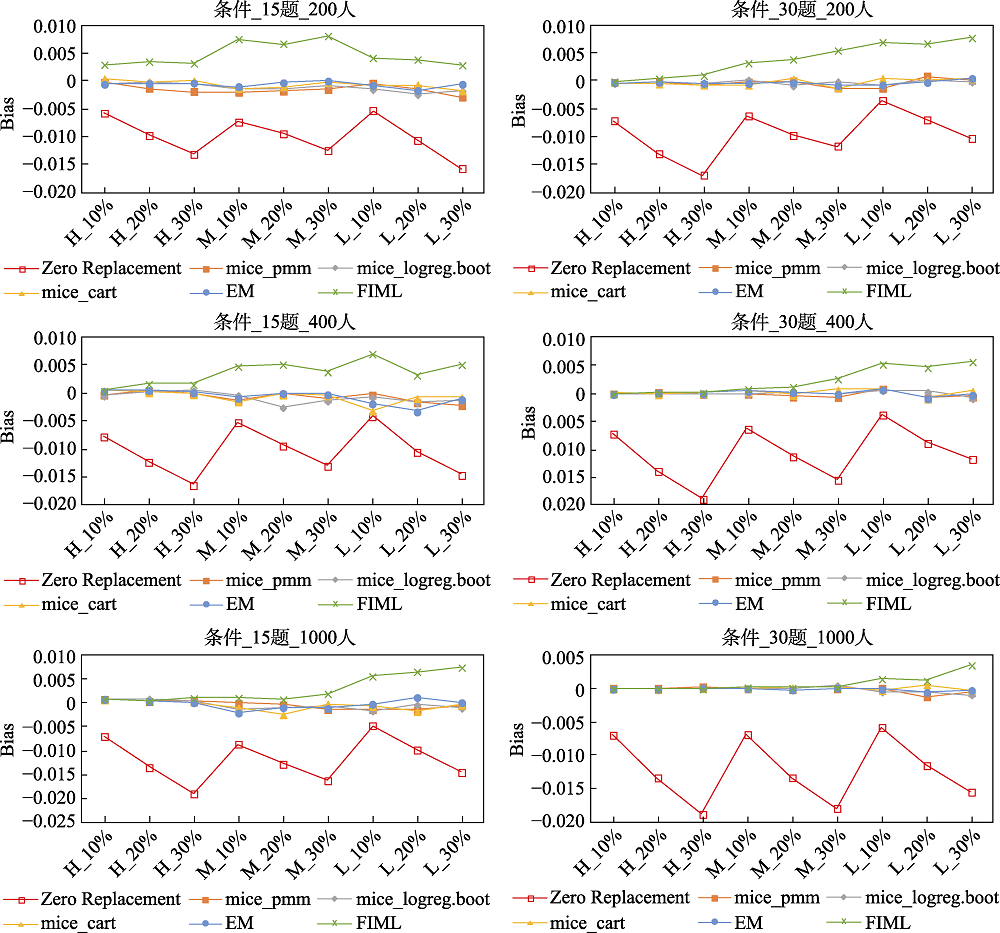
图1 不同处理方法下题目参数的Bias (MAR机制) 注:横坐标条件中第一个字母表示题目质量(H: 高质量, M: 中等质量, L: 低质量), 第二个数字表示缺失率(10%, 20%, 30%)。Zero Replacement代表零替换法, mice-pmm, mice-logreg.boot, mice-cart依次代表了多重插补中的预测均值匹配, 基于Bootstrap的贝叶斯逻辑回归和分类回归树法, EM代表期望最大化法, FIML代表了全息极大似然估计法。
| 处理方法 | 参考指标 | ||||
|---|---|---|---|---|---|
| Cor | Deviance (-2LL) | AIC | BIC | SE | |
| ZR | 0.804 | 4345.98 | 4411.98 | 4563.77 | 0.256 |
| MI-PMM | 0.793 | 4633.08 | 4648.78 | 4800.58 | 0.243 |
| MI-LOGREG.BOOT | 0.800 | 4170.47 | 4347.45 | 4499.24 | 0.263 |
| MI-CART | 0.756 | 4628.56 | 4694.79 | 4846.59 | 0.268 |
| EM | 0.809 | 4343.13 | 4409.13 | 4560.93 | 0.258 |
| FIML | 0.808 | 4169.45 | 4235.45 | 4387.25 | 0.260 |
表1 实证研究结果1
| 处理方法 | 参考指标 | ||||
|---|---|---|---|---|---|
| Cor | Deviance (-2LL) | AIC | BIC | SE | |
| ZR | 0.804 | 4345.98 | 4411.98 | 4563.77 | 0.256 |
| MI-PMM | 0.793 | 4633.08 | 4648.78 | 4800.58 | 0.243 |
| MI-LOGREG.BOOT | 0.800 | 4170.47 | 4347.45 | 4499.24 | 0.263 |
| MI-CART | 0.756 | 4628.56 | 4694.79 | 4846.59 | 0.268 |
| EM | 0.809 | 4343.13 | 4409.13 | 4560.93 | 0.258 |
| FIML | 0.808 | 4169.45 | 4235.45 | 4387.25 | 0.260 |
| 处理方法 | 绝对拟合指标 | ||||
|---|---|---|---|---|---|
| M2 | df | p | RMSEA2 | 90%CI | |
| ZR | 16.69 | 12 | 0.162 | 0.023 | [0,0.047] |
| MI-PMM | 13.81 | 12 | 0.313 | 0.014 | [0,0.042] |
| MI-LOGREG.BOOT | 22.54 | 12 | 0.032 | 0.035 | [0.01,0.056] |
| MI-CART | 22.14 | 12 | 0.036 | 0.034 | [0.009,0.056] |
| EM | 17.19 | 12 | 0.143 | 0.024 | [0,0.048] |
| FIML | 22.64 | 12 | 0.031 | 0.035 | [0.01,0.057] |
表2 实证研究结果2
| 处理方法 | 绝对拟合指标 | ||||
|---|---|---|---|---|---|
| M2 | df | p | RMSEA2 | 90%CI | |
| ZR | 16.69 | 12 | 0.162 | 0.023 | [0,0.047] |
| MI-PMM | 13.81 | 12 | 0.313 | 0.014 | [0,0.042] |
| MI-LOGREG.BOOT | 22.54 | 12 | 0.032 | 0.035 | [0.01,0.056] |
| MI-CART | 22.14 | 12 | 0.036 | 0.034 | [0.009,0.056] |
| EM | 17.19 | 12 | 0.143 | 0.024 | [0,0.048] |
| FIML | 22.64 | 12 | 0.031 | 0.035 | [0.01,0.057] |
| 处理方法 | 参考指标 | ✔的 总数 | 排序 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Cor | -2LL | AIC | BIC | SE | p | RMESA2 | |||
| ZR | ✔ | ✔ | ✔ | ✔ | 4 | 2 | |||
| MI-PMM | ✔ | ✔ | ✔ | 3 | 3 | ||||
| MI-LOGREG.BOOT | ✔ | ✔ | ✔ | 3 | 3 | ||||
| MI-CART | 0 | 4 | |||||||
| EM | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | 7 | 1 |
| FIML | ✔ | ✔ | ✔ | ✔ | 4 | 2 | |||
表3 实证研究结果汇总
| 处理方法 | 参考指标 | ✔的 总数 | 排序 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Cor | -2LL | AIC | BIC | SE | p | RMESA2 | |||
| ZR | ✔ | ✔ | ✔ | ✔ | 4 | 2 | |||
| MI-PMM | ✔ | ✔ | ✔ | 3 | 3 | ||||
| MI-LOGREG.BOOT | ✔ | ✔ | ✔ | 3 | 3 | ||||
| MI-CART | 0 | 4 | |||||||
| EM | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | 7 | 1 |
| FIML | ✔ | ✔ | ✔ | ✔ | 4 | 2 | |||
| 属性 | 题目 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
表1 模拟研究Q矩阵(5属性15题目条件)
| 属性 | 题目 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 属性 | 题目 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 属性 | 题目 | ||||||||||||||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 4 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
表2 模拟研究Q矩阵(5属性30题目条件)
| 属性 | 题目 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 属性 | 题目 | ||||||||||||||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 4 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 属性 | 题目 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CM033Q01 | CM474Q01 | CM155Q01 | CM155Q04 | CM411Q01 | CM411Q02 | CM803Q01 | CM442Q02 | CM034Q01 | |
| ${{\alpha }_{1}}$ | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| ${{\alpha }_{2}}$ | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| ${{\alpha }_{3}}$ | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| ${{\alpha }_{4}}$ | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
表3 实证研究Q矩阵
| 属性 | 题目 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CM033Q01 | CM474Q01 | CM155Q01 | CM155Q04 | CM411Q01 | CM411Q02 | CM803Q01 | CM442Q02 | CM034Q01 | |
| ${{\alpha }_{1}}$ | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| ${{\alpha }_{2}}$ | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| ${{\alpha }_{3}}$ | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| ${{\alpha }_{4}}$ | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| [1] |
Akaike, H. (1974). A new look at the statistical model identification. IEEE transactions on automatic control, 19(6), 716-723.
doi: 10.1109/TAC.1974.1100705 URL |
| [2] | Bai, S. (2020). Developing a learning progression for probability based on the GDINA model in China. Frontiers in Psychology, 11, 2561. |
| [3] |
Chen, L., Savalei, V., & Rhemtulla, M. (2020). Two-stage maximum likelihood approach for item-level missing data in regression. Behavior Research Methods, 52(6), 2306-2323.
doi: 10.3758/s13428-020-01355-x URL |
| [4] | Dai, S. (2017). Investigation of missing responses in implementation of cognitive diagnostic models (Unpublished doctorial dissertation). Indiana University. |
| [5] |
de Ayala, R. J., Plake, B. S., & Impara, J. C. (2001). The impact of omitted responses on the accuracy of ability estimation in item response theory. Journal of Educational Measurement, 38(3), 213-234.
doi: 10.1111/jedm.2001.38.issue-3 URL |
| [6] | de la Torre, J. (2009). DINA model and parameter estimation:A didactic. Journal of Educational and Behavioral Statistics, 34(1), 115-130. |
| [7] |
de la Torre, J. (2011). The generalized DINA model framework. Psychometrika, 76(2), 179-199.
doi: 10.1007/s11336-011-9207-7 URL |
| [8] |
Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological), 39(1), 1-22.
doi: 10.1111/rssb.1977.39.issue-1 URL |
| [9] |
Dong, Y., & Peng, C. Y. J. (2013). Principled missing data methods for researchers. SpringerPlus, 2(1), 1-17.
doi: 10.1186/2193-1801-2-1 URL |
| [10] |
Eekhout, I., Enders, C. K., Twisk, J. W., de Boer, M. R., de Vet, H. C., & Heymans, M. W. (2015). Analyzing incomplete item scores in longitudinal data by including item score information as auxiliary variables. Structural Equation Modeling: A Multidisciplinary Journal, 22(4), 588-602.
doi: 10.1080/10705511.2014.937670 URL |
| [11] | Enders, C. K. (2010). Applied missing data analysis. Guilford press. |
| [12] |
Finch, H. (2008). Estimation of item response theory parameters in the presence of missing data. Journal of Educational Measurement, 45(3), 225-245.
doi: 10.1111/jedm.2008.45.issue-3 URL |
| [13] | Gao, X., Wang, D., Cai, Y., & Tu, D. (2018). Comparison of CDM and its selection: A saturated model, a simple model or a mixed method. Journal of Psychological Science, 41(3), 727-734. |
| [ 高旭亮, 汪大勋, 蔡艳, 涂冬波. (2018). 认知诊断模型的比较及其应用研究: 饱和模型、简化模型还是混合方法. 心理科学, 41(3), 727-734.] | |
| [14] |
Graham, J. W. (2009). Missing data analysis: Making it work in the real world. Annual Review of Psychology, 60, 549-576.
doi: 10.1146/annurev.psych.58.110405.085530 pmid: 18652544 |
| [15] |
Graham, J. W., Olchowski, A. E., & Gilreath, T. D. (2007). How many imputations are really needed? Some practical clarifications of multiple imputation theory. Prevention Science, 8(3), 206-213.
doi: 10.1007/s11121-007-0070-9 pmid: 17549635 |
| [16] |
Guo, L., & Zhou, W. (2021). Nonparametric methods for cognitive diagnosis to multiple-choice test items. Acta Psychologica Sinica, 53(9), 1032-1043.
doi: 10.3724/SP.J.1041.2021.01032 URL |
| [ 郭磊, 周文杰. (2021). 基于选项层面的认知诊断非参数方法. 心理学报, 53(9), 1032-1043.] | |
| [17] | Huisman, M., & Molenaar, I.W. (2001). Imputation of missing scale data with item response models. In: A. Boomsma, M. A. J. van Duijn, & T. A. B. Snijders (Eds.), Lecture Notes in Statistics: Vol. 157: Essays on Item Response Theory (pp. 221-244). Springer. |
| [18] |
Jang, E. E. (2009). Cognitive diagnostic assessment of L2 reading comprehension ability: Validity arguments for Fusion Model application to LanguEdge assessment. Language Testing, 26(1), 31-73.
doi: 10.1177/0265532208097336 URL |
| [19] |
Jeličić, H., Phelps, E., & Lerner, R. M. (2010). Why missing data matter in the longitudinal study of adolescent development: Using the 4-H Study to understand the uses of different missing data methods. Journal of Youth and Adolescence, 39(7), 816-835.
doi: 10.1007/s10964-010-9542-5 URL |
| [20] |
Junker, B. W., & Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25(3), 258-272.
doi: 10.1177/01466210122032064 URL |
| [21] |
Kaya, Y., & Leite, W. L. (2017). Assessing change in latent skills across time with longitudinal cognitive diagnosis modeling: An evaluation of model performance. Educational and Psychological Measurement, 77(3), 369-388.
doi: 10.1177/0013164416659314 URL |
| [22] | Leacy, F. P., Floyd, S., Yates, T. A., & White, I. R. (2017). Analyses of sensitivity to the missing-at-random assumption using multiple imputation with delta adjustment: application to a tuberculosis/HIV prevalence survey with incomplete HIV-status data. American Journal of Epidemiology, 185(4), 304-315. |
| [23] |
Lee, Y.-S., Park, Y. S., & Taylan, D. (2011). A cognitive diagnostic modeling of attribute mastery in Massachusetts, Minnesota, and the U.S. national sample using the TIMSS 2007. International Journal of Testing, 11(2), 144-177.
doi: 10.1080/15305058.2010.534571 URL |
| [24] | Lin, T. H. (2010). A comparison of multiple imputation with EM algorithm and MCMC method for quality of life missing data. Quality & Quantity, 44(2), 277-287. |
| [25] | Liu, Y., Tian, W., & Xin, T. (2016). An application of M2 statistic to evaluate the fit of cognitive diagnostic models. Journal of Educational and Behavioral Statistics, 41(1), 3-26. |
| [26] |
Liu, Y., Xin, T., Andersson, B., & Tian, W. (2019). Information matrix estimation procedures for cognitive diagnostic models. British Journal of Mathematical and Statistical Psychology, 72(1), 18-37.
doi: 10.1111/bmsp.2019.72.issue-1 URL |
| [27] |
Liu, Y., Xin, T., Li, L., Tian, W., & Liu, X. (2016). An improved method for differential item functioning detection in cognitive diagnosis models: an application of Wald statistic based on observed information matrix. Acta Psychologica Sinica, 48(5), 588-598.
doi: 10.3724/SP.J.1041.2016.00588 URL |
| [ 刘彦楼, 辛涛, 李令青, 田伟, 刘笑笑. (2016). 改进的认知诊断模型项目功能差异检验方法--基于观察信息矩阵的Wald统计量. 心理学报, 48(5), 588-598.] | |
| [28] | Ma, W., & de la Torre, J. (2020). GDINA: An R package for cognitive diagnosis modeling. Journal of Statistical Software, 93(14), 1-26. |
| [29] |
Ma, W., & de la Torre, J. (2016). A sequential cognitive diagnosis model for polytomous responses. British Journal of Mathematical and Statistical Psychology, 69(3), 253-275.
doi: 10.1111/bmsp.2016.69.issue-3 URL |
| [30] |
Ma, W., Iaconangelo, C., & de la Torre, J. (2016). Model similarity, model selection, and attribute classification. Applied Psychological Measurement, 40(3), 200-217.
doi: 10.1177/0146621615621717 URL |
| [31] |
Marshall, A., Altman, D. G., Royston, P., & Holder, R. L. (2010). Comparison of techniques for handling missing covariate data within prognostic modelling studies: A simulation study. BMC Medical Research Methodology, 10(1), 1-16.
doi: 10.1186/1471-2288-10-1 URL |
| [32] |
Mazza, G. L., Enders, C. K., & Ruehlman, L. S. (2015). Addressing item-level missing data: A comparison of proration and full information maximum likelihood estimation. Multivariate Behavioral Research, 50(5), 504-519.
doi: 10.1080/00273171.2015.1068157 pmid: 26610249 |
| [33] | Nájera, P., Abad, F. J., & Sorrel, M. A. (2021). Determining the number of attributes in cognitive diagnosis modeling. Frontiers in Psychology, 12, 321. |
| [34] |
Newman, D. A. (2003). Longitudinal modeling with randomly and systematically missing data: A simulation of ad hoc, maximum likelihood, and multiple imputation techniques. Organizational Research Methods, 6(3), 328-362.
doi: 10.1177/1094428103254673 URL |
| [35] |
Pan, Y., & Zhan, P. (2020). The impact of sample attrition on longitudinal learning diagnosis: A Prolog. Frontiers in Psychology, 11, 1051.
doi: 10.3389/fpsyg.2020.01051 URL |
| [36] |
Rezvan, P. H., Lee, K. J., & Simpson, J. A. (2015). The rise of multiple imputation: A review of the reporting and implementation of the method in medical research. BMC Medical Research Methodology, 15(1), 1-14.
doi: 10.1186/1471-2288-15-1 URL |
| [37] |
Rubin, D. B. (1976). Inference and missing data. Biometrika, 63(3), 581-592.
doi: 10.1093/biomet/63.3.581 URL |
| [38] |
Schafer, J. L., & Graham, J. W. (2002). Missing data: Our view of the state of the art. Psychological Methods, 7(2), 147-177.
pmid: 12090408 |
| [39] | Schwarz, G. (1978). Estimating the Dimension of a Model. The Annals of Statistics, 6(2), 461-464. |
| [40] |
Shan, N., & Wang, X. (2020). Cognitive diagnosis modeling incorporating item-level missing data mechanism. Frontiers in Psychology, 11, 564707.
doi: 10.3389/fpsyg.2020.564707 URL |
| [41] | van Buuren, S. (2018). Flexible imputation of missing data, Second Edition. Chapman and Hall/CRC. |
| [42] | van Buuren, S., & Groothuis-Oudshoorn, K. (2011). mice: Multivariate Imputation by Chained Equations in R. Journal of Statistical Software, 45(3), 1-67. |
| [43] | Wothke, W. (2000). Longitudinal and multigroup modeling with missing data. In T. D. Little, K. U. Schnabel, & J. Baumert (Eds.), Modeling longitudinal and multilevel data (pp. 205-224). Psychology Press. |
| [44] |
Xiao, J., & Bulut, O. (2020). Evaluating the performances of missing data handling methods in ability estimation from sparse data. Educational and Psychological Measurement, 80(5), 932-954.
doi: 10.1177/0013164420911136 URL |
| [45] |
Xu, X., de la Torre, J., Zhang, J., Guo, J., & Shi, N. (2020). Estimating CDMs using the slice-within-gibbs sampler. Frontiers in Psychology, 11, 2260.
doi: 10.3389/fpsyg.2020.02260 URL |
| [46] | Xu, X., & von Davier, M. (2006). Cognitive diagnosis for NAEP proficiency data. ETS Research Report Series,(1), 1-25. |
| [47] |
Ye, S. J., Tang, W. Q., Zhang, M. Q., & Cao, M. C. (2004). Techniques for missing data in longitudinal studies and its application. Advances in Psychological Science, 22(12), 1985-1994.
doi: 10.3724/SP.J.1042.2014.01985 URL |
| [ 叶素静, 唐文清, 张敏强, 曹魏聪. (2014). 追踪研究中缺失数据处理方法及应用现状分析. 心理科学进展, 22(12), 1985-1994.] | |
| [48] |
Zhang, S., & Wang, S. (2018). Modeling learner heterogeneity: A mixture learning model with responses and response times. Frontiers in Psychology, 9, 2339.
doi: 10.3389/fpsyg.2018.02339 pmid: 30568609 |
| [1] | 谭青蓉, 蔡艳, 汪大勋, 罗芬, 涂冬波. CD-CAT中基于SCAD惩罚和EM视角的在线标定方法开发——G-DINA模型[J]. 心理学报, 2024, 56(5): 670-688. |
| [2] | 郭磊, 秦海江. 基于信号检测论的认知诊断评估:构建与应用[J]. 心理学报, 2024, 56(3): 339-351. |
| [3] | 田亚淑, 詹沛达, 王立君. 联合作答精度和作答时间的概率态认知诊断模型[J]. 心理学报, 2023, 55(9): 1573-1586. |
| [4] | 游晓锋, 杨建芹, 秦春影, 刘红云. 认知诊断测评中缺失数据的处理:随机森林阈值插补法[J]. 心理学报, 2023, 55(7): 1192-1206. |
| [5] | 刘彦楼, 陈启山, 王一鸣, 姜晓彤. 模型参数点估计的可靠性:以CDM为例[J]. 心理学报, 2023, 55(10): 1712-1728. |
| [6] | 刘彦楼, 吴琼琼. 认知诊断模型Q矩阵修正:完整信息矩阵的作用[J]. 心理学报, 2023, 55(1): 142-158. |
| [7] | 孙小坚, 郭磊. 考虑题目选项信息的非参数认知诊断计算机自适应测验[J]. 心理学报, 2022, 54(9): 1137-1150. |
| [8] | 李佳, 毛秀珍, 韦嘉. 一种简单有效的Q矩阵修正新方法[J]. 心理学报, 2022, 54(8): 996-1008. |
| [9] | 刘彦楼. 认知诊断模型的标准误与置信区间估计:并行自助法[J]. 心理学报, 2022, 54(6): 703-724. |
| [10] | 詹沛达. 引入眼动注视点的联合-交叉负载多模态认知诊断建模[J]. 心理学报, 2022, 54(11): 1416-1423. |
| [11] | 郭磊, 周文杰. 基于选项层面的认知诊断非参数方法[J]. 心理学报, 2021, 53(9): 1032-1043. |
| [12] | 谭青蓉, 汪大勋, 罗芬, 蔡艳, 涂冬波. 一种高效的CD-CAT在线标定新方法:基于熵的信息增益与EM视角[J]. 心理学报, 2021, 53(11): 1286-1300. |
| [13] | 罗芬, 王晓庆, 蔡艳, 涂冬波. 基于基尼指数的双目标CD-CAT选题策略[J]. 心理学报, 2020, 52(12): 1452-1465. |
| [14] | 汪大勋, 高旭亮, 蔡艳, 涂冬波. 基于类别水平的多级计分认知诊断Q矩阵修正:相对拟合统计量视角[J]. 心理学报, 2020, 52(1): 93-106. |
| [15] | 詹沛达, 于照辉, 李菲茗, 王立君. 一种基于多阶认知诊断模型测评科学素养的方法[J]. 心理学报, 2019, 51(6): 734-746. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||