

CN 11-1911/B
主办:中国心理学会
中国科学院心理研究所
出版:科学出版社


心理学报 ›› 2024, Vol. 56 ›› Issue (6): 714-730.doi: 10.3724/SP.J.1041.2024.00714 cstr: 32110.14.2024.00714
蒋家丽1,2, 戚玥3, 雷秀雅1, 卢骊霏1, 于晓1( )
)
收稿日期:2023-01-04
发布日期:2024-04-08
出版日期:2024-06-25
通讯作者:
于晓, E-mail: yx0903yingzhong@163.com基金资助:
JIANG Jiali1,2, QI Yue3, LEI Xiuya1, LU Lifei1, YU Xiao1( )
)
Received:2023-01-04
Online:2024-04-08
Published:2024-06-25
摘要:
为了揭示符号和非符号空间−数字反应编码联合效应(spatial-numerical association of response codes, SNARC效应)各自的发展规律及二者关系, 实验1以36名6~7岁儿童、59名7~8岁儿童、69名8~9岁儿童和31名成人为被试, 测查符号和非符号奇偶判断任务, 发现符号SNARC效应在8~9岁儿童中才出现, 但非符号SNARC效应在6~7岁儿童中就已出现, 且跨年龄组(儿童和成人)的数据和针对儿童的追踪数据分析显示两种SNARC效应在一定年龄范围内可能并不会随着年龄的增长而发生变化。此外, 对于同时出现符号与非符号SNARC效应的8~9岁儿童和成人来说, 符号和非符号SNARC效应相关不显著。为进一步探讨两种SNARC效应是否有相似的认知机制, 实验2对137名8~9岁儿童进行为期半年的追踪, 测查其言语能力(语音意识、语音记忆和快速命名)、视空间能力(视知觉和心理旋转)、工作记忆(言语工作记忆和视空间工作记忆)及符号和非符号SNARC效应, 结果显示: 言语能力和言语工作记忆对符号SNARC效应预测作用显著, 视空间能力和视空间工作记忆对非符号SNARC效应预测显著。这表明两种SNARC效应具有不同的认知基础。研究结果支持了符号与非符号SNARC效应的分离假说, 并拓展了双编码理论。
中图分类号:
蒋家丽, 戚玥, 雷秀雅, 卢骊霏, 于晓. (2024). 符号与非符号空间−数字反应编码联合效应的发展:言语能力、视空间能力和工作记忆的作用. 心理学报, 56(6), 714-730.
JIANG Jiali, QI Yue, LEI Xiuya, LU Lifei, YU Xiao. (2024). The development of symbolic and non-symbolic SNARC effects: The roles of phonological abilities, visuospatial abilities and working memory. Acta Psychologica Sinica, 56(6), 714-730.
| 量级 | 反应手 | 符号奇偶判断任务 | 非符号奇偶判断任务 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 6~7岁 | 7~8岁 | 8~9岁 | 成人 | 6~7岁 | 7~8岁 | 8~9岁 | 成人 | |||
| 非常小 | 右手 | M | 1629.90 | 1146.11 | 1062.31 | 613.06 | 1560.70 | 1124.46 | 1166.23 | 740.10 |
| SD | 336.59 | 298.49 | 215.52 | 88.47 | 388.00 | 261.27 | 278.37 | 107.14 | ||
| 左手 | M | 1579.23 | 1039.76 | 930.81 | 531.05 | 1396.31 | 1049.99 | 1042.01 | 646.35 | |
| SD | 348.54 | 240.21 | 212.45 | 66.49 | 271.92 | 198.65 | 201.40 | 43.78 | ||
| dRT | M | 50.67 | 106.34 | 132.35 | 82.01 | 164.38 | 74.47 | 134.12 | 93.75 | |
| 小 | 右手 | M | 1778.45 | 1142.37 | 1040.21 | 581.29 | 1623.44 | 1137.55 | 1175.93 | 717.83 |
| SD | 445.36 | 276.32 | 231.75 | 73.68 | 436.73 | 254.54 | 339.13 | 150.63 | ||
| 左手 | M | 1705.85 | 1140.12 | 970.47 | 537.19 | 1557.71 | 1097.82 | 1142.37 | 653.57 | |
| SD | 389.96 | 359.88 | 177.77 | 62.63 | 450.18 | 269.35 | 274.72 | 105.48 | ||
| dRT | M | 72.60 | 2.25 | 66.00 | 44.10 | 65.73 | 39.73 | 43.35 | 64.26 | |
| 大 | 右手 | M | 1839.24 | 1226.57 | 1032.03 | 541.04 | 1871.93 | 1529.89 | 1355.14 | 859.76 |
| SD | 543.33 | 335.68 | 280.26 | 76.76 | 703.93 | 423.48 | 397.46 | 167.72 | ||
| 左手 | M | 1797.23 | 1207.98 | 1092.73 | 600.98 | 1980.72 | 1618.86 | 1544.99 | 935.03 | |
| SD | 542.33 | 290.52 | 239.77 | 80.67 | 712.47 | 441.28 | 475.06 | 254.15 | ||
| dRT | M | 42.01 | 18.59 | −54.51 | −59.94 | −108.79 | −88.97 | −167.16 | −75.27 | |
| 非常大 | 右手 | M | 1880.88 | 1238.13 | 985.64 | 532.51 | 1926.38 | 1536.89 | 1584.18 | 913.06 |
| SD | 389.51 | 377.97 | 224.89 | 63.19 | 676.96 | 512.58 | 520.09 | 208.92 | ||
| 左手 | M | 1770.35 | 1121.94 | 1056.61 | 640.67 | 2127.60 | 1800.97 | 1697.88 | 994.68 | |
| SD | 383.87 | 272.76 | 239.75 | 107.38 | 708.18 | 564.96 | 421.46 | 235.54 | ||
| dRT | M | 110.53 | 116.18 | −68.02 | −108.17 | −201.23 | −264.07 | −120.56 | −81.62 | |
表1 各年龄组在符号与非符号奇偶判断任务中的左右手平均反应时(ms)
| 量级 | 反应手 | 符号奇偶判断任务 | 非符号奇偶判断任务 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 6~7岁 | 7~8岁 | 8~9岁 | 成人 | 6~7岁 | 7~8岁 | 8~9岁 | 成人 | |||
| 非常小 | 右手 | M | 1629.90 | 1146.11 | 1062.31 | 613.06 | 1560.70 | 1124.46 | 1166.23 | 740.10 |
| SD | 336.59 | 298.49 | 215.52 | 88.47 | 388.00 | 261.27 | 278.37 | 107.14 | ||
| 左手 | M | 1579.23 | 1039.76 | 930.81 | 531.05 | 1396.31 | 1049.99 | 1042.01 | 646.35 | |
| SD | 348.54 | 240.21 | 212.45 | 66.49 | 271.92 | 198.65 | 201.40 | 43.78 | ||
| dRT | M | 50.67 | 106.34 | 132.35 | 82.01 | 164.38 | 74.47 | 134.12 | 93.75 | |
| 小 | 右手 | M | 1778.45 | 1142.37 | 1040.21 | 581.29 | 1623.44 | 1137.55 | 1175.93 | 717.83 |
| SD | 445.36 | 276.32 | 231.75 | 73.68 | 436.73 | 254.54 | 339.13 | 150.63 | ||
| 左手 | M | 1705.85 | 1140.12 | 970.47 | 537.19 | 1557.71 | 1097.82 | 1142.37 | 653.57 | |
| SD | 389.96 | 359.88 | 177.77 | 62.63 | 450.18 | 269.35 | 274.72 | 105.48 | ||
| dRT | M | 72.60 | 2.25 | 66.00 | 44.10 | 65.73 | 39.73 | 43.35 | 64.26 | |
| 大 | 右手 | M | 1839.24 | 1226.57 | 1032.03 | 541.04 | 1871.93 | 1529.89 | 1355.14 | 859.76 |
| SD | 543.33 | 335.68 | 280.26 | 76.76 | 703.93 | 423.48 | 397.46 | 167.72 | ||
| 左手 | M | 1797.23 | 1207.98 | 1092.73 | 600.98 | 1980.72 | 1618.86 | 1544.99 | 935.03 | |
| SD | 542.33 | 290.52 | 239.77 | 80.67 | 712.47 | 441.28 | 475.06 | 254.15 | ||
| dRT | M | 42.01 | 18.59 | −54.51 | −59.94 | −108.79 | −88.97 | −167.16 | −75.27 | |
| 非常大 | 右手 | M | 1880.88 | 1238.13 | 985.64 | 532.51 | 1926.38 | 1536.89 | 1584.18 | 913.06 |
| SD | 389.51 | 377.97 | 224.89 | 63.19 | 676.96 | 512.58 | 520.09 | 208.92 | ||
| 左手 | M | 1770.35 | 1121.94 | 1056.61 | 640.67 | 2127.60 | 1800.97 | 1697.88 | 994.68 | |
| SD | 383.87 | 272.76 | 239.75 | 107.38 | 708.18 | 564.96 | 421.46 | 235.54 | ||
| dRT | M | 110.53 | 116.18 | −68.02 | −108.17 | −201.23 | −264.07 | −120.56 | −81.62 | |
| 任务类型 | 年龄组 | ||||
|---|---|---|---|---|---|
| 6~7岁 | 7~8岁 | 8~9岁 | 成人 | ||
| 符号奇偶判断任务 | M ± SD | 8.27 ± 46.66 | 6.40 ± 52.90 | −26.60 ± 46.64 | −29.90 ± 16.88 |
| t | 1.06 | −0.87 | −4.53*** | −9.86*** | |
| 非符号奇偶判断任务 | M ± SD | −53.15 ± 75.89 | −53.77 ± 73.85 | −46.16 ± 78.69 | −29.85 ± 30.31 |
| t | −4.20*** | −5.50*** | −4.84*** | −5.48*** | |
表2 每种任务类型下斜率的单样本t检验结果
| 任务类型 | 年龄组 | ||||
|---|---|---|---|---|---|
| 6~7岁 | 7~8岁 | 8~9岁 | 成人 | ||
| 符号奇偶判断任务 | M ± SD | 8.27 ± 46.66 | 6.40 ± 52.90 | −26.60 ± 46.64 | −29.90 ± 16.88 |
| t | 1.06 | −0.87 | −4.53*** | −9.86*** | |
| 非符号奇偶判断任务 | M ± SD | −53.15 ± 75.89 | −53.77 ± 73.85 | −46.16 ± 78.69 | −29.85 ± 30.31 |
| t | −4.20*** | −5.50*** | −4.84*** | −5.48*** | |
| 任务 | M ± SD | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 T2非符号Slope | −18.89 ± 72.70 | − | |||||||||
| 2 T2符号Slope | −13.37 ± 44.22 | −0.06 | − | ||||||||
| 3 T1视空间工作记忆 | 3.42 ± 1.15 | 0.41*** | 0.03 | − | |||||||
| 4 T1言语工作记忆 | 4.44 ± 1.70 | −0.04 | 0.29** | 0.35** | − | ||||||
| 5 T1语音记忆 | 6.39 ± 1.47 | −0.03 | −0.33** | 0.16 | 0.18* | − | |||||
| 6 T1快速自动命名 | 15.44 ± 4.04 | 0.03 | 0.34** | 0.32** | −0.15 | −0.22** | − | ||||
| 7 T1语音意识 | 31.67 ± 8.25 | 0.10 | −0.28** | 0.06 | 0.04 | 0.28** | −0.12 | − | |||
| 8 T1三维心理旋转 | 13.42 ± 2.80 | −0.37** | −0.01 | −0.08 | 0.11 | 0.03 | 0.13 | 0.08 | − | ||
| 9 T1视知觉 | 64.9 ± 33.45 | −0.33** | 0.15 | −0.16 | 0.20* | 0.10 | 0.17 | 0.14 | 0.30** | − | |
| 10 T1非符号Slope | −12.64 ± 97.55 | 0.26** | 0.02 | 0.23** | 0.02 | 0.09 | 0.01 | −0.13 | 0.24** | −0.11 | − |
| 11 T1符号Slope | −9.39 ± 76.26 | 0.17 | 0.03 | −0.02 | 0.17 | 0.06 | 0.19* | −0.26** | −0.03 | −0.12 | −0.06 |
表3 儿童在各变量上描述性统计及相关结果(N = 137)
| 任务 | M ± SD | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 T2非符号Slope | −18.89 ± 72.70 | − | |||||||||
| 2 T2符号Slope | −13.37 ± 44.22 | −0.06 | − | ||||||||
| 3 T1视空间工作记忆 | 3.42 ± 1.15 | 0.41*** | 0.03 | − | |||||||
| 4 T1言语工作记忆 | 4.44 ± 1.70 | −0.04 | 0.29** | 0.35** | − | ||||||
| 5 T1语音记忆 | 6.39 ± 1.47 | −0.03 | −0.33** | 0.16 | 0.18* | − | |||||
| 6 T1快速自动命名 | 15.44 ± 4.04 | 0.03 | 0.34** | 0.32** | −0.15 | −0.22** | − | ||||
| 7 T1语音意识 | 31.67 ± 8.25 | 0.10 | −0.28** | 0.06 | 0.04 | 0.28** | −0.12 | − | |||
| 8 T1三维心理旋转 | 13.42 ± 2.80 | −0.37** | −0.01 | −0.08 | 0.11 | 0.03 | 0.13 | 0.08 | − | ||
| 9 T1视知觉 | 64.9 ± 33.45 | −0.33** | 0.15 | −0.16 | 0.20* | 0.10 | 0.17 | 0.14 | 0.30** | − | |
| 10 T1非符号Slope | −12.64 ± 97.55 | 0.26** | 0.02 | 0.23** | 0.02 | 0.09 | 0.01 | −0.13 | 0.24** | −0.11 | − |
| 11 T1符号Slope | −9.39 ± 76.26 | 0.17 | 0.03 | −0.02 | 0.17 | 0.06 | 0.19* | −0.26** | −0.03 | −0.12 | −0.06 |
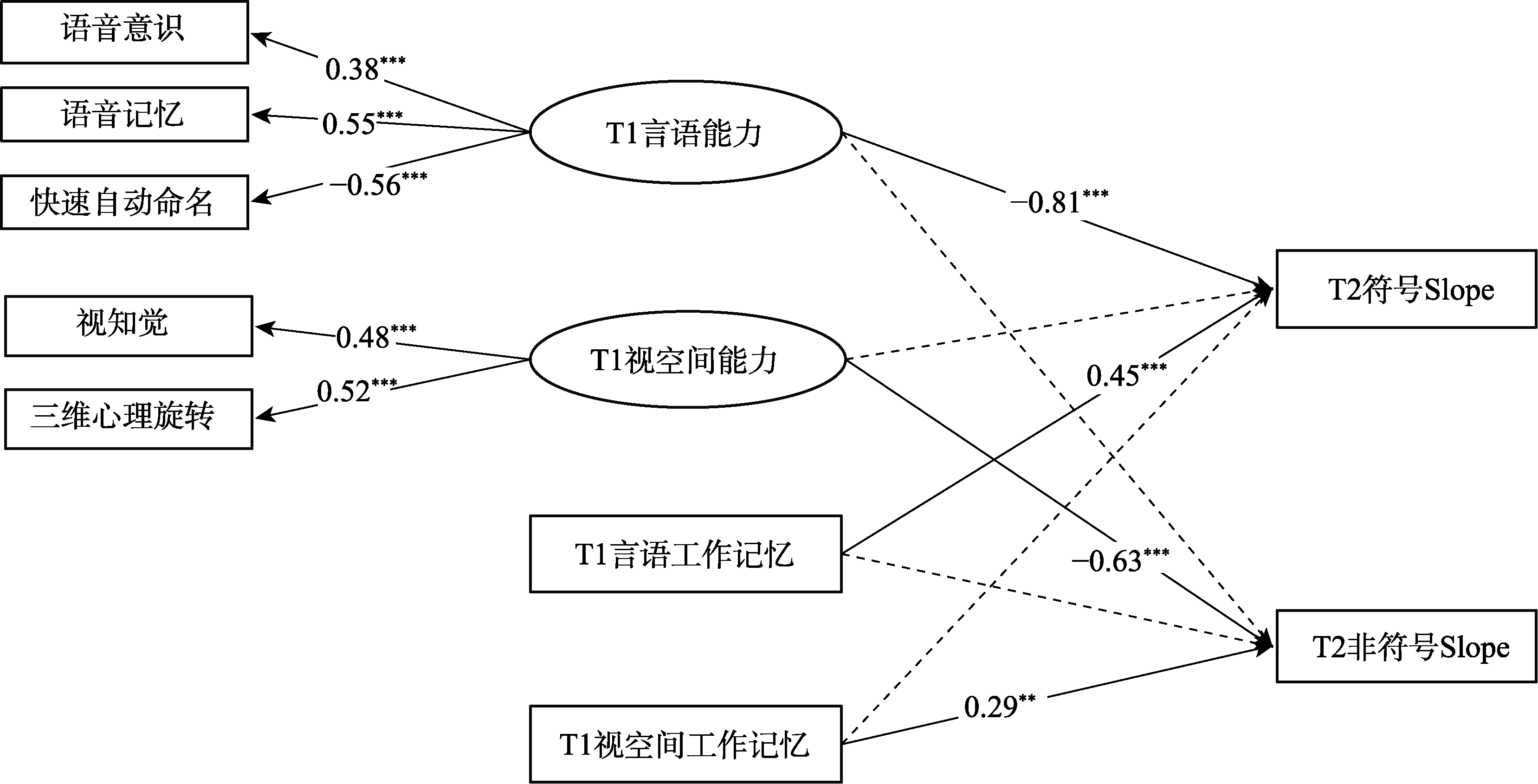
图12 路径分析模型图 注: (1)模型采用回归斜率Slope作为符号与非符号SNARC效应的指标, SNARC效应越强, Slope分数越小; 此外, 控制了T1阶段的符号与非符号SNARC效应。(2)实线表示路径显著, 虚线表示路径不显著, 路径上的数值为标准化的回归系数。(3)**代表p < 0.01; ***代表p < 0.001。
| [1] | Aulet, L. S., & Lourenco, S. F. (2018). The developing mental number line: Does its directionality relate to 5- to 7-year-old children’s mathematical abilities? Frontiers in Psychology, 9, Article 1142. |
| [2] | Bachot, J., Gevers, W., Fias, W., & Roeyers, H. (2005). Number sense in children with visuospatial disabilities: Orientation of the mental number line. Psychology Science, 47(1), 172-183. |
| [3] |
Baddeley, A. (2003). Working memory and language: An overview. Journal of Communication Disorders, 36(3), 189-208.
doi: 10.1016/s0021-9924(03)00019-4 pmid: 12742667 |
| [4] |
Berch, D. B., Foley, E. J., Hill, R. J., & Ryan, P. M. (1999). Extracting parity and magnitude from Arabic numerals: Developmental changes in number processing and mental representation. Journal of Experimental Child Psychology, 74(4), 286-308.
doi: 10.1006/jecp.1999.2518 pmid: 10552920 |
| [5] |
Bulf, H., de Hevia, M. D., & Macchi Cassia, V. (2016). Small on the left, large on the right: Numbers orient visual attention onto space in preverbal infants. Developmental Science, 19(3), 394-401.
doi: 10.1111/desc.12315 pmid: 26074348 |
| [6] |
Chan, W. W. L., & Wong, T. T. (2016). The underlying number-space mapping among kindergarteners and its relation with early numerical abilities. Journal of Experimental Child Psychology, 148, 35-50.
doi: 10.1016/j.jecp.2016.03.010 pmid: 27104240 |
| [7] |
Chen, Y., Wang, J., Kirk, R. M., Pethtel, O. L., & Kiefner, A. E. (2014). Age differences in adaptive decision making: The role of numeracy. Educational Gerontology, 40(11), 825-833.
pmid: 25544800 |
| [8] | Cheng, C., & Kibbe, M. M. (2023). Is nonsymbolic arithmetic truly “arithmetic”? Examining the computational capacity of the approximate number system in young children. Cognitive Science, 47(6), e13299. |
| [9] | Cipora, K., Haman, M., Domahs, F., & Nuerk, H. (2020). Editorial: On the development of space-number relations: linguistic and cognitive determinants, influences, and associations. Frontiers in Psychology, 11, Article 182. |
| [10] | Cutini, S., Aleotti, S., Di Bono, M. G., & Priftis, K. (2019). Order versus chaos: The impact of structure on number- space associations. Attention, Perception, & Psychophysics, 81( 6), 1781-1788. |
| [11] |
de Hevia, M. D., Veggiotti, L., Streri, A., & Bonn, C. D. (2017). At birth, humans associate “few” with left and “many” with right. Current Biology, 27(24), 3879-3884.
doi: 10.1016/j.cub.2017.11.024 |
| [12] | Dehaene, S., Bossini, S., & Giraux, P. (1993). The mental representation of parity and number magnitude. Journal of Experimental Psychology: General, 122(3), 371-396. |
| [13] | Dehaene, S., Dupoux, E., & Mehler, J. (1990). Is numerical comparison digital? Analogical and symbolic effects in two-digit number comparison. Journal of Experimental Psychology: Human Perception and Performance, 16(3), 626-641. |
| [14] | Deng, Z., Chen, Y., Zhang, M., Li, Y., & Zhu, X. (2018). The association of number and space under different tasks: Insight from a process perspective. Frontiers in Psychology, 9, Article 957. |
| [15] | Deng, Z. J., Chen, Y. H., Zhu, X. S., & Li, Y. J. (2017). The effect of working memory load on the SNARC effect: Maybe tasks have a word to say. Memory & Cognition, 45(3), 428-441. |
| [16] | Di Giorgio, E., Lunghi, M., Rugani, R., Regolin, L., Dalla Barba, B., Vallortigara, G., & Simion, F. (2019). A mental number line in human newborns. Developmental Science, 22(6), e12801. |
| [17] | Dollman, J., & Levine, W. H. (2016). Rapid communication the mental number line dominates alternative, explicit coding of number magnitude. The Quarterly Journal of Experimental Psychology, 69(3), 403-409. |
| [18] |
Ebersbach, M., Luwel, K., & Verschaffel, L. (2014). Further evidence for a spatial-numerical association in children before formal schooling. Experimental Psychology, 61(4), 323-329.
doi: 10.1027/1618-3169/a000250 pmid: 24351987 |
| [19] | Escobar, J., Porflitt, F., & Ceric, F. (2021). Evaluating the rapid automatized naming and arithmetical fluency relationship in Chilean first grade students. Educational Psychology (Dorchester-on-Thames), 41(6), 730-747. |
| [20] | Fias, W., Brysbaert, M., Geypens, F., & Ydewalle, G. D. (1996). The importance of magnitude information in numerical processing: Evidence from the SNARC effect. Mathematical Cognition, 2(1), 95-110. |
| [21] | Fias, W., & Fischer, M. H. (2005). Spatial representation of numbers. In J. I. D. Campbell (Ed.), Handbook of mathematical cognition (pp. 43-54). New York: Psychology Press. |
| [22] |
Fischer, M. H., & Shaki, S. (2016). Measuring spatial- numerical associations: Evidence for a purely conceptual link. Psychological Research, 80(1), 109-112.
doi: 10.1007/s00426-015-0646-0 pmid: 25617061 |
| [23] | Formoso, J., Barreyro, J. P., Jacubovich, S., & Injoque-Ricle, I. (2017). Possible associations between subitizing, estimation and visuospatial working memory (VSWM) in children. The Spanish Journal of Psychology, 20, e27. |
| [24] | Gardner, M. F. (1996). Test of visual-perceptual skills (non-motor) revised. New York: Psychological and Educational Publications. |
| [25] |
Gazes, R. P., Diamond, R. F. L., Hope, J. M., Caillaud, D., Stoinski, T. S., & Hampton, R. R. (2017). Spatial representation of magnitude in gorillas and orangutans. Cognition, 168, 312-319.
doi: S0010-0277(17)30213-5 pmid: 28772188 |
| [26] |
Gebuis, T., Cohen Kadosh, R., De Haan, E., & Henik, A. (2009). Automatic quantity processing in 5-year olds and adults. Cognitive Processing, 10(2), 133-142.
doi: 10.1007/s10339-008-0219-x pmid: 18607652 |
| [27] | Gevers, W., Caessens, B., & Fias, W. (2005). Towards a common processing architecture underlying Simon and SNARC effects. European Journal of Cognitive Psychology, 17(5), 659-673. |
| [28] |
Gevers, W., Lammertyn, J., Notebaert, W., Verguts, T., & Fias, W. (2006). Automatic response activation of implicit spatial information: Evidence from the SNARC effect. Acta Psychologica, 122(3), 221-233.
pmid: 16423320 |
| [29] | Gevers, W., Santens, S., Dhooge, E., Chen, Q., Van den Bossche, L., Fias, W., & Verguts, T. (2010). Verbal-spatial and visuospatial coding of number-space interactions. Journal of Experimental Psychology General, 139(1), 180-190. |
| [30] |
Gibson, L. C., & Maurer, D. (2016). Development of SNARC and distance effects and their relation to mathematical and visuospatial abilities. Journal of Experimental Child Psychology, 150, 301-313.
doi: S0022-0965(16)30040-6 pmid: 27376924 |
| [31] |
Girelli, L., Lucangeli, D., & Butterworth, B. (2000). The development of automaticity in accessing number magnitude. Journal of Experimental Child Psychology, 76(2), 104-122.
pmid: 10788305 |
| [32] |
He, X., Guo, P., Li, S., Shen, X., & Zhou, X. (2021). Non-symbolic and symbolic number lines are dissociated. Cognitive Processing, 22(3), 475-486.
doi: 10.1007/s10339-021-01019-4 pmid: 33751283 |
| [33] |
Herrera, A. Macizo, P., & Semenza, C. (2008). The role of working memory in the association between number magnitude and space. Acta Psychologica, 128(2), 225-237.
doi: 10.1016/j.actpsy.2008.01.002 pmid: 18295166 |
| [34] |
Hoffmann, D., Pigat, D., & Schiltz, C. (2014). The impact of inhibition capacities and age on number-space associations. Cognitive Processing, 15(3), 329-342.
doi: 10.1007/s10339-014-0601-9 pmid: 24442798 |
| [35] |
Imbo, I., de Brauwer, J., Fias, W., & Gevers, W. (2012). The development of the SNARC effect: Evidence for early verbal coding. Journal of Experimental Child Psychology, 111(4), 671-680.
doi: 10.1016/j.jecp.2011.09.002 pmid: 22024386 |
| [36] | Jonas, C. N., Spiller, M. J., Jansari, A., & Ward, J. (2014). Comparing implicit and synaesthetic number-space associations: Visuospatial and verbal spatial-numerical associations of response codes. The Quarterly Journal of Experimental Psychology, 67(7), 1262-1273. |
| [37] |
Karbach, J., Strobach, T., & Schubert, T. (2015). Adaptive working-memory training benefits reading, but not mathematics in middle childhood. Child Neuropsychology, 21(3), 285-301.
doi: 10.1080/09297049.2014.899336 pmid: 24697256 |
| [38] | Kirby, J. R., Parrila, R. K., & Pfeiffer, S. L. (2003). Naming speed and phonological awareness as predictors of reading development. Journal of Educational Psychology, 95(3), 453-464. |
| [39] | Knoch, D., Brugger, P., & Regard, M. (2004). Suppressing versus releasing a habit: Frequency-dependent effects of prefrontal transcranial magnetic stimulation. Cerebral Cortex, 15(7), 885-887. |
| [40] |
Krajewski, K., & Schneider, W. (2009). Exploring the impact of phonological awareness, visual-spatial working memory, and preschool quantity-number competencies on mathematics achievement in elementary school: Findings from a 3-year longitudinal study. Journal of Experimental Child Psychology, 103(4), 516-531.
doi: 10.1016/j.jecp.2009.03.009 pmid: 19427646 |
| [41] |
Lourenco, S. F., & Longo, M. R. (2010). General magnitude representation in human infants. Psychological Science, 21(6), 873-881.
doi: 10.1177/0956797610370158 pmid: 20431048 |
| [42] | Nemeh, F., Humberstone, J., Yates, M. J., & Reeve, R. A. (2018). Non-symbolic magnitudes are represented spatially: Evidence from a non-symbolic SNARC task. PLoS ONE, 13(8), e203019. |
| [43] | Noël, M. P., Seron, X., & Trovarelli, F. (2003). Working memory as a predictor of addition skills and addition strategies in children. Current Psychology of Cognition, 22(1), 3-24. |
| [44] | Nuerk, H., Wood, G., & Willmes, K. (2005). The universal SNARC effect: The association between number magnitude and space is amodal. Experimental Psychology, 52(3), 187-194. |
| [45] | Núñez-Peña, M. I., Colomé, À., & González-Gómez, B. (2021). The spatial-numerical association of response codes (SNARC) effect in highly math-anxious individuals: An ERP study. Biological Psychology, 161, 108062. |
| [46] | Paivio, A. (1986). Mental representations: A dual coding approach. New York: Oxford University Press. |
| [47] | Pan, Y., Han, X., Mei, G., Bai, X., & Chen, Y. (2019). Development of number-space associations: SNARC effects and spatial attention in 7- to 11-year-olds. PLoS ONE, 14(3), e212204. |
| [48] |
Passolunghi, M. C., & Costa, H. M. (2016). Working memory and early numeracy training in preschool children. Child Neuropsychology, 22(1), 81-98.
doi: 10.1080/09297049.2014.971726 pmid: 25366543 |
| [49] |
Patro, K., & Haman, M. (2012). The spatial-numerical congruity effect in preschoolers. Journal of Experimental Child Psychology, 111(3), 534-542.
doi: 10.1016/j.jecp.2011.09.006 pmid: 22153910 |
| [50] |
Peters, L., Polspoel, B., de Beeck, H. O., & De Smedt, B. (2016). Brain activity during arithmetic in symbolic and non-symbolic formats in 9-12 year old children. Neuropsychologia, 86, 19-28.
doi: 10.1016/j.neuropsychologia.2016.04.001 pmid: 27044845 |
| [51] |
Proctor, R. W., & Cho, Y. S. (2006). Polarity correspondence: A general principle for performance of speeded binary classification tasks. Psychological Bulletin, 132(3), 416-442.
pmid: 16719568 |
| [52] | Prpic, V., Basamh, Y. A., Goodridge, C. M., Agostini, T., & Murgia, M. (2023). Contrasting symbolic and non-symbolic numerical representations in a joint classification task. Psychonomic Bulletin & Review, 30, 1422-1430. |
| [53] |
Prpic, V., Fumarola, A., De Tommaso, M., Luccio, R., Murgia, M., & Agostini, T. (2016). Separate mechanisms for magnitude and order processing in the spatial-numerical association of response codes (SNARC) effect: The strange case of musical note values. Journal of Experimental Psychology: Human Perception and Performance, 42(8), 1241-1251.
doi: 10.1037/xhp0000217 pmid: 26950384 |
| [54] |
Prpic, V., Soranzo, A., Santoro, I., Fantoni, C., Galmonte, A., Agostini, T., & Murgia, M. (2020). SNARC-like compatibility effects for physical and phenomenal magnitudes: A study on visual illusions. Psychological Research, 84(4), 950-965.
doi: 10.1007/s00426-018-1125-1 pmid: 30511158 |
| [55] |
Sasanguie, D., De Smedt, B., & Reynvoet, B. (2017). Evidence for distinct magnitude systems for symbolic and non- symbolic number. Psychological Research, 81(1), 231-242.
doi: 10.1007/s00426-015-0734-1 pmid: 26708496 |
| [56] |
Shepard, R. N., & Metzler, J. (1971). Mental rotation of three-dimensional objects. Science, 171(3972), 701-703.
doi: 10.1126/science.171.3972.701 pmid: 5540314 |
| [57] | Toomarian, E. Y., & Hubbard, E. M. (2018). On the genesis of spatial-numerical associations: Evolutionary and cultural factors co-construct the mental number line. Neuroscience & Biobehavioral Reviews, 90, 184-199. |
| [58] |
Tosto, M. G., Hanscombe, K. B., Haworth, C. M., Davis, O. S., Petrill, S. A., Dale, P. S., ... Kovas, Y. (2014). Why do spatial abilities predict mathematical performance? Developmental Science, 17(3), 462-470.
doi: 10.1111/desc.12138 pmid: 24410830 |
| [59] | Tzelgov, J., Meyer, J., & Henik, A. (1992). Automatic and intentional processing of numerical information. Journal of Experimental Psychology: Learning, Memory, and Cognition, 18( 1), 166-179. |
| [60] | van Dijck, J. P., & Fias, W. (2011). A working memory account for spatial-numerical associations. Cognition, 119(l),114-119. |
| [61] |
van Galen, M. S., & Reitsma, P. (2008). Developing access to number magnitude: A study of the SNARC effect in 7- to 9-year-olds. Journal of Experimental Child Psychology, 101(2), 99-113.
doi: 10.1016/j.jecp.2008.05.001 pmid: 18602112 |
| [62] |
Van Garderen, D. (2006). Spatial visualization, visual imagery, and mathematical problem solving of students with varying abilities. Journal of Learning Disabilities, 39(6), 496-506.
pmid: 17165617 |
| [63] | Viarouge, A., Hubbard, E. M., & McCandliss, B. D. (2014). The cognitive mechanisms of the SNARC effect: An individual differences approach. PLoS One, 9(4), e95756. |
| [64] | Wagner, R. K., & Torgesen, J. K. (1987). The nature of phonological processing and its causal role in the acquisition of reading skills. Psychological Bulletin, 101(2), 192-212. |
| [65] |
Wang, Q. Q., Zhang, Q., Shi, W. D., Wang, Z. W., & Zhang, Z. P. (2022). Online construction of spatial representation of numbers: Evidence from the SNARC effect in number processing in interferential situations. Acta Psychologica Sinica, 54(7), 761-771.
doi: 10.3724/SP.J.1041.2022.00761 |
|
[王强强, 张琦, 石文典, 王志伟, 章鹏程. (2022). 数字空间表征的在线建构: 来自干扰情境中数字SNARC效应的证据. 心理学报, 54(7), 761-771.]
doi: 10.3724/SP.J.1041.2022.00761 |
|
| [66] | White, S. L. J., Dénes, S., & Fruzsina, S. (2012). Symbolic number: The integration of magnitude and spatial representations in children aged 6 to 8 years. Frontiers in Psychology, 2, Article 392. |
| [67] | Wood, G., Willmes, K., Nuerk, H., & Fischer, M. H. (2008). On the cognitive link between space and number: A meta-analysis of the SNARC effect. Psychology Science Quarterly, 50(4), 489-525. |
| [68] | Wright, I., Waterman, M., Prescott, H., & Murdoch-Eaton, D. (2003). A new Stroop-like measure of inhibitory function development: typical developmental trends. Journal of Child Psychology Psychiatry, 44(4), 561-575. |
| [69] | Wu, H., Yang, X., Geng, L., Zhu, X., & Chen, Y. (2020). How do working memory and inhibition contribute to the SNARC effect in Chinese school-aged children? Cognitive Development, 56, 100959. |
| [70] |
Xu, X., Chen, C., Pan, M., & Li, N. (2013). Development of numerical estimation in Chinese preschool children. Journal of Experimental Child Psychology, 116(2), 351-366.
doi: 10.1016/j.jecp.2013.06.009 pmid: 23933179 |
| [71] |
Yan, L. Z., Chen, Y. X., Liu, X., Fu, S. M., & Nan, W. Z. (2022). The flexibility of spatial-numerical associations and its internal mechanism. Advances in Psychological Science, 30(1), 51-64.
doi: 10.3724/SP.J.1042.2022.00051 |
| [颜丽珠, 陈妍秀, 刘勋, 傅世敏, 南威治. (2022). 数字空间联结的灵活性及其内在机制. 心理科学进展, 30(1), 1-14.] | |
| [72] |
Yang, T., Chen, C., Zhou, X., Xu, J., Dong, Q., & Chen, C. (2014). Development of spatial representation of numbers: A study of the SNARC effect in Chinese children. Journal of Experimental Child Psychology, 117, 1-11.
doi: 10.1016/j.jecp.2013.08.011 pmid: 24121228 |
| [73] | Yang, X., Huo, S., & Zhang, X. (2021). Visual-spatial skills contribute to Chinese reading and arithmetic for different reasons: A three-wave longitudinal study. Journal of Experimental Child Psychology, 208, Article 105142. |
| [74] | Yang, X., & McBride, C. (2020). How do phonological processing abilities contribute to early Chinese reading and mathematics? Educational Psychology (Dorchester-on- Thames), 40(7), 893-911. |
| [75] | Yang, X., Peng, P., & Meng, X. (2019). How do metalinguistic awareness, working memory, reasoning, and inhibition contribute to Chinese character reading of kindergarten children? Infant and Child Development, 28(3), e2122. |
| [76] |
Yang, X., & Yu, X. (2021). The relationship between mental rotation and arithmetic: do number line estimation, working memory, or place-value concept matter? British Journal of Educational Psychology, 91(3), 793-810.
doi: 10.1111/bjep.12403 pmid: 33368175 |
| [77] | Yang, X., Zhang, X., Huo, S., & Zhang, Y. (2020). Differential contributions of cognitive precursors to symbolic versus non-symbolic numeracy in young Chinese children. Early Childhood Research Quarterly, 53, 208-216. |
| [78] | Zhang, X., & Lin, D. (2015). Pathways to arithmetic: The role of visual-spatial and language skills in written arithmetic, arithmetic word problems, and nonsymbolic arithmetic. Contemporary Educational Psychology, 41, 188-197. |
| [79] | Zhang, Y., Chen, C., Liu, H., Cui, J., & Zhou, X. (2016). Both non-symbolic and symbolic quantity processing are important for arithmetical computation but not for mathematical reasoning. Journal of Cognitive Psychology, 28(7), 807-824. |
| [80] | Zhou, X., Chen, Y., Chen, C., Jiang, T., Zhang, H., & Dong, Q. (2007). Chinese kindergartners' automatic processing of numerical magnitude in Stroop-like tasks. Memory & Cognition, 35(3), 464-470. |
| [81] | Zhou, X., Hu, Y., Yuan, L., Gu, T., & Li, D. (2020). Visual form perception predicts 3-year longitudinal development of mathematical achievement. Cognitive Processing. 21(4), 521-532. |
| [1] | 吴三美, 田良苏, 陈家侨, 陈广耀, 王敬欣. 中文阅读中无关言语效应的认知机制探究:眼动证据[J]. 心理学报, 2021, 53(7): 729-745. |
| [2] | 闫嵘,俞国良. 小学学习不良儿童言语交际策略理解水平及其发展特点[J]. 心理学报, 2009, 41(07): 602-612. |
| [3] | 聂衍刚,林崇德,彭以松,丁莉,甘秀英. 青少年社会适应行为的发展特点[J]. 心理学报, 2008, 40(09): 1013-1020. |
| [4] | 杨丽珠,王江洋,刘文,Monica Cuskelly,Airong Zhang. 3~5岁幼儿自我延迟满足的发展特点及其中澳跨文化比较[J]. 心理学报, 2005, 37(02): 224-232. |
| [5] | 董奇,陶沙,曾琦,芦咏莉,王雁萍. 8─11个月婴儿迂回行为发展特点与学习能力的研究[J]. 心理学报, 1997, 29(3): 286-293. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||