

CN 11-4766/R
主办:中国科学院心理研究所
出版:科学出版社


心理科学进展 ›› 2024, Vol. 32 ›› Issue (10): 1736-1756.doi: 10.3724/SP.J.1042.2024.01736 cstr: 32111.14.2024.01736
• 研究方法 • 上一篇
收稿日期:2023-06-25
出版日期:2024-10-15
发布日期:2024-08-13
通讯作者:
郭鸣谦, E-mail: mqguo30@gmail.com;
GUO Mingqian1( ), PAN Wanke2, HU Chuanpeng2(
), PAN Wanke2, HU Chuanpeng2( )
)
Received:2023-06-25
Online:2024-10-15
Published:2024-08-13
摘要:
认知建模近年来在科学心理学获得广泛应用, 而模型比较是认知建模中关键的一环: 研究者需要通过模型比较选择出最优模型, 才能进行后续的假设检验或潜变量推断。模型比较不仅要考虑模型对数据的拟合(平衡过拟合与欠拟合), 也需要考虑模型的复杂度。然而, 模型比较指标众多, 纷繁复杂, 给研究者的选用带来困难。本文将认知建模常用的模型比较指标分为三大类并介绍其计算方法及优劣, 包括拟合优度指标(包括均方误差、决定系数、ROC曲线等)、基于交叉验证的指标(包括AIC、DIC等)和基于边际似然的指标。结合正交Go/No-Go范式的公开数据, 本文展示各指标在R语言中如何实现。在此基础上, 本文探讨各指标的适用情境及模型平均等新思路。
中图分类号:
郭鸣谦, 潘晚坷, 胡传鹏. (2024). 认知建模中模型比较的方法. 心理科学进展 , 32(10), 1736-1756.
GUO Mingqian, PAN Wanke, HU Chuanpeng. (2024). Model comparison in cognitive modeling. Advances in Psychological Science, 32(10), 1736-1756.
| 拟合度指标 | 适用的参数估计方法 | 优点 | 缺点 |
|---|---|---|---|
| 均方误差(MSE) | 极大似然法、最小二乘法 | 直观简单, 易于计算和解释 | 不适用于分类问题, 未考虑模型复杂度对过拟合的影响 |
| 决定系数( | 极大似然法、最小二乘法 | 衡量模型变量变异性占比, 提供模型拟合的可解释性 | 对模型的复杂性敏感, 无法比较特征数目不同的模型 |
| 对数似然函数 | 极大似然法, 最大后验概率法, 贝叶斯参数估计 | 反映模型预测与实际数据的匹配程度, 可用于模型比较和参数估计; MSE和 | 不适用于非概率、非参数模型; 对异常值敏感 |
| ROC曲线 | 极大似然法, 最大后验概率法, 贝叶斯参数估计 | 用于评估模型对实际数据的预测能力。 | 不适用于数据为多选项的情况; 对于不平衡数据, 结果不够准确 |
| 后验预测检查 | 贝叶斯参数估计 | 考虑参数不确定性和模型复杂性; 可检查对新数据样本的预测能力 | 需要领域专业知识对先验和后验分布进行假设; 计算复杂度较高 |
表1 各拟合度指标的优缺点以及适用的参数估计范围
| 拟合度指标 | 适用的参数估计方法 | 优点 | 缺点 |
|---|---|---|---|
| 均方误差(MSE) | 极大似然法、最小二乘法 | 直观简单, 易于计算和解释 | 不适用于分类问题, 未考虑模型复杂度对过拟合的影响 |
| 决定系数( | 极大似然法、最小二乘法 | 衡量模型变量变异性占比, 提供模型拟合的可解释性 | 对模型的复杂性敏感, 无法比较特征数目不同的模型 |
| 对数似然函数 | 极大似然法, 最大后验概率法, 贝叶斯参数估计 | 反映模型预测与实际数据的匹配程度, 可用于模型比较和参数估计; MSE和 | 不适用于非概率、非参数模型; 对异常值敏感 |
| ROC曲线 | 极大似然法, 最大后验概率法, 贝叶斯参数估计 | 用于评估模型对实际数据的预测能力。 | 不适用于数据为多选项的情况; 对于不平衡数据, 结果不够准确 |
| 后验预测检查 | 贝叶斯参数估计 | 考虑参数不确定性和模型复杂性; 可检查对新数据样本的预测能力 | 需要领域专业知识对先验和后验分布进行假设; 计算复杂度较高 |
| 指标 | 适用的参数估计方法 | 优点 | 缺点 |
|---|---|---|---|
| AIC* | 极大似然法, 最大后验概率法, 贝叶斯参数估计 | 计算简便, 在任何参数估计情况下都可使用 | 对交叉验证的近似准确程度不如后三者 |
| DIC* | 贝叶斯参数估计 | 计算简便, 绝大多数贝叶斯统计软件均提供了该指标 | 没有利用贝叶斯参数估计得到的整个参数后验分布 |
| WAIC* | 贝叶斯参数估计 | 对交叉似然的近似更精确 | 容易受到MCMC采样极端值影响 |
| PSIS-Loo-CV* | 贝叶斯参数估计 | 对交叉似然的近似更精确 | 容易受到MCMC采样极端值影响 |
表2 各交叉验证近似指标的优缺点以及适用的参数估计范围。
| 指标 | 适用的参数估计方法 | 优点 | 缺点 |
|---|---|---|---|
| AIC* | 极大似然法, 最大后验概率法, 贝叶斯参数估计 | 计算简便, 在任何参数估计情况下都可使用 | 对交叉验证的近似准确程度不如后三者 |
| DIC* | 贝叶斯参数估计 | 计算简便, 绝大多数贝叶斯统计软件均提供了该指标 | 没有利用贝叶斯参数估计得到的整个参数后验分布 |
| WAIC* | 贝叶斯参数估计 | 对交叉似然的近似更精确 | 容易受到MCMC采样极端值影响 |
| PSIS-Loo-CV* | 贝叶斯参数估计 | 对交叉似然的近似更精确 | 容易受到MCMC采样极端值影响 |
| 指标 | 适用的参数估计方法 | 优点 | 缺点 |
|---|---|---|---|
| BIC* | 极大似然法, 最大后验概率法, 贝叶斯参数估计。 | 计算简便, 在任何参数估计情况下都可使用。 | 没有先验的影响, 对边际似然的近似不如后四者。 |
| KDE | 贝叶斯参数估计。 | 计算较采样方法更为简便。 | 较少有研究使用。没有工具包, 需要研究者手动实践。 |
| 拉普拉斯近似* | 极大似然法, 最大后验概率法, 贝叶斯参数估计。 | 在任何参数估计情况下都可使用。 | 海森矩阵有可能为NaN值。没有工具包, 需要研究者手动实践。 |
| 重要性采样 | 贝叶斯参数估计。 | 较桥采样计算简便。 | 容易受到MCMC采样极端值影响。 |
| 桥采样* | 贝叶斯参数估计。 | 对边际似然的近似比较精准。 | 计算步骤复杂, 只有R包bridgesampling提供了简便的使用接口 |
表3 各边际似然近似指标的优缺点以及适用的参数估计范围。
| 指标 | 适用的参数估计方法 | 优点 | 缺点 |
|---|---|---|---|
| BIC* | 极大似然法, 最大后验概率法, 贝叶斯参数估计。 | 计算简便, 在任何参数估计情况下都可使用。 | 没有先验的影响, 对边际似然的近似不如后四者。 |
| KDE | 贝叶斯参数估计。 | 计算较采样方法更为简便。 | 较少有研究使用。没有工具包, 需要研究者手动实践。 |
| 拉普拉斯近似* | 极大似然法, 最大后验概率法, 贝叶斯参数估计。 | 在任何参数估计情况下都可使用。 | 海森矩阵有可能为NaN值。没有工具包, 需要研究者手动实践。 |
| 重要性采样 | 贝叶斯参数估计。 | 较桥采样计算简便。 | 容易受到MCMC采样极端值影响。 |
| 桥采样* | 贝叶斯参数估计。 | 对边际似然的近似比较精准。 | 计算步骤复杂, 只有R包bridgesampling提供了简便的使用接口 |
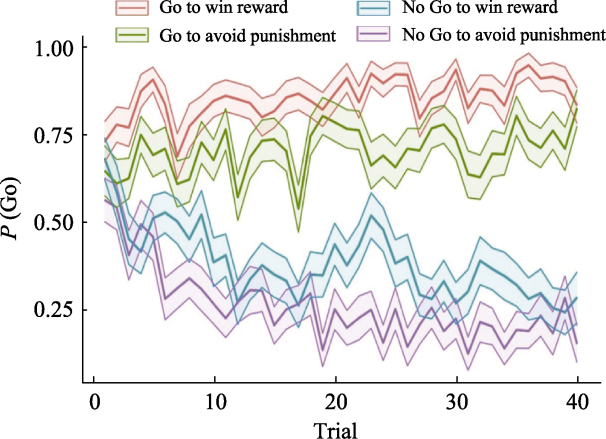
图5 案例Trial-by-trial的行为数据。图中横坐标是试次数量, 纵坐标是选择Go反应的比例。4种颜色代表4种cue。彩图见电子版。随着试次数量的增大, 个体行为逐渐变得稳定, 这体现工具性学习的作用。而获得奖赏和避免惩罚cue下, 个体Go反应的比例的不对称性则体现巴浦洛夫效应。具体而言, 个体更易有Go反应去获得奖赏, 但是却更多地有No Go反应去避免惩罚。
| [1] |
胡传鹏, 孔祥祯, Wagenmakers, E.-J., Ly, A., 彭凯平. (2018). 贝叶斯因子及其在JASP中的实现. 心理科学进展, 26(6), 951-965. https://doi.org/10.3724/sp.J.1042.2018.00951
doi: 10.3724/SP.J.1042.2018.00951 URL |
| [2] |
区健新, 吴寅, 刘金婷, 李红. (2020). 计算精神病学: 抑郁症研究和临床应用的新视角. 心理科学进展, 28(1), 111-127. https://doi.org/10.3724/sp.J.1042.2020.00111
doi: 10.3724/SP.J.1042.2020.00111 URL |
| [3] | 王允宏, van den Berg, D., Aust, F., Ly, A., Wagenmaker, E.-J., 胡传鹏,(2023). 贝叶斯方差分析在JASP中的实现. 心理技术与应用, 11(9), 528-541. http://dx.doi.org/10.16842/j.cnki.issn2095-5588.2023.09.002 |
| [4] | Acerbi, L., Dokka, K., Angelaki, D. E., & Ma, W. J. (2018). Bayesian comparison of explicit and implicit causal inference strategies in multisensory heading perception. PLoS Computational Biololgy, 14(7), e1006110. https://doi.org/10.1371/journal.pcbi.1006110 |
| [5] | Ahn, W. Y., Haines, N., & Zhang, L. (2017). Revealing neurocomputational mechanisms of reinforcement learning and decision-making with the hBayesDM package. Computational Psychiatry, 1, 24-57. https://doi.org/10.1162/CPSY_a_00002 |
| [6] | Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), 716-723. https://doi.org/10.1109/TAC.1974.1100705 |
| [7] | Anderson, D., & Burnham, K. (2004). Model selection and multi-model inference. (Vol 63). Springer. |
| [8] |
Ballard, I. C., Wagner, A. D., & McClure, S. M. (2019). Hippocampal pattern separation supports reinforcement learning. Nature Communications, 10(1), 1073. https://doi.org/10.1038/s41467-019-08998-1
doi: 10.1038/s41467-019-08998-1 URL pmid: 30842581 |
| [9] |
Betts, M. J., Richter, A., de Boer, L., Tegelbeckers, J., Perosa, V., Baumann, V., ... Krauel, K. (2020). Learning in anticipation of reward and punishment: Perspectives across the human lifespan. Neurobiology of Aging, 96, 49-57. https://doi.org/10.1016/j.neurobiolaging.2020.08.011
doi: S0197-4580(20)30267-0 URL pmid: 32937209 |
| [10] | Bishop, C. M. (2006). Pattern recognition and machine learning. Springer. |
| [11] | Blei, D. M., Kucukelbir, A., & McAuliffe, J. D. (2017). Variational inference: A review for statisticians. Journal of the American Statistical Association, 112(518), 859-877. https://doi.org/10.1080/01621459.2017.1285773 |
| [12] | Boehm, U., Annis, J., Frank, M. J., Hawkins, G. E., Heathcote, A., Kellen, D., ... Wagenmakers, E.-J. (2018). Estimating across-trial variability parameters of the Diffusion Decision Model: Expert advice and recommendations. Journal of Mathematical Psychology, 87, 46-75. https://doi.org/10.1016/j.jmp.2018.09.004 |
| [13] | Boehm, U., Evans, N. J., Gronau, Q. F., Matzke, D., Wagenmakers, E.-J., & Heathcote, A. J. (2023). Inclusion Bayes factors for mixed hierarchical diffusion decision models. Psychological Methods. https://doi.org/10.1037/met0000582 Bos, C. S. (2002). A comparison of marginal likelihood computation methods. In: Härdle, W., & Rönz, B. (Eds.), Compstat:Physica, Heidelberg. |
| [14] |
Brown, S. D., & Heathcote, A. (2008). The simplest complete model of choice response time: linear ballistic accumulation. Cognitive Psychology, 57(3), 153-178. https://doi.org/10.1016/j.cogpsych.2007.12.002
doi: 10.1016/j.cogpsych.2007.12.002 URL pmid: 18243170 |
| [15] | Burnham, K. P., & Anderson, D. R. (2004). Multimodel inference: Understanding AIC and BIC in model selection. Sociological Methods & Research, 33(2), 261-304. https://doi.org/10.1177/0049124104268644 |
| [16] | Carpenter, B., Gelman, A., Hoffman, M. D., Lee, D., Goodrich, B., Betancourt, M., ... Riddell, A. (2017). Stan: A probabilistic programming language. Journal of Statistical Software, 76(1), 1-32. https://doi.org/10.18637/jss.v076.i01 |
| [17] | Casella, G., & Berger, R. L. (2002). Statistical inference. Cengage Learning. |
| [18] | Cavanagh, J. F., Eisenberg, I., Guitart-Masip, M., Huys, Q., & Frank, M. J. (2013). Frontal theta overrides pavlovian learning biases. The Journal of Neuroscience, 33(19), 8541-8548. https://doi.org/10.1523/JNEUROSCI.5754-12.2013 |
| [19] | Clyde, M. A., Ghosh, J., & Littman, M. L. (2011). Bayesian adaptive sampling for variable selection and model averaging. Journal of Computational and Graphical Statistics, 20(1), 80-101. https://doi.org/10.1198/jcgs.2010.09049 |
| [20] |
Collins, A. G., & Frank, M. J. (2012). How much of reinforcement learning is working memory, not reinforcement learning? A behavioral, computational, and neurogenetic analysis. European Journal Of Neuroscience, 35(7), 1024-1035. https://doi.org/10.1111/j.1460-9568.2011.07980.x
doi: 10.1111/j.1460-9568.2011.07980.x URL pmid: 22487033 |
| [21] | Collins, A. G. E., & Frank, M. J. (2018). Within- and across- trial dynamics of human EEG reveal cooperative interplay between reinforcement learning and working memory. Proceedings of the National Academy of Sciences, 115(10), 2502-2507. https://doi.org/10.1073/pnas.1720963115 |
| [22] | Daniel, R., Radulescu, A., & Niv, Y. (2020). Intact reinforcement learning but impaired attentional control during multidimensional probabilistic learning in older adults. The Journal of Neuroscience, 40(5), 1084-1096. https://doi.org/10.1523/JNEUROSCI.0254-19.2019 |
| [23] | Daunizeau, J., Adam, V., & Rigoux, L. (2014). VBA: A probabilistic treatment of nonlinear models for neurobiological and behavioural data. PLoS Computational Biology, 10(1), e1003441. https://doi.org/10.1371/journal.pcbi.1003441 |
| [24] | Davis, J., & Goadrich, M. (2006). The relationship between Precision-Recall and ROC curves. Proceedings of the 23rd international conference on Machine learning, Pittsburgh, Pennsylvania, USA. https://doi.org/10.1145/1143844.1143874 |
| [25] | Daw, N. D. (2011). Trial-by-trial data analysis using computational models. In Delgado, M. R. (Ed.), Decision making, affect, learning: Attention performance XXIII (Vol. 23, pp. 3-38). Oxford University Press. |
| [26] |
Dayan, P., Niv, Y., Seymour, B., & Daw, N. D. (2006). The misbehavior of value and the discipline of the will. Neural Networks, 19(8), 1153-1160. https://doi.org/10.1016/j.neunet.2006.03.002
URL pmid: 16938432 |
| [27] | Devine, S., Falk, C. F., & Fujimoto, K. A. (2023). Comparing the accuracy of three predictive information criteria for Bayesian linear multilevel model selection. PsyArXiv. https://doi.org/10.31234/osf.io/p2n8a |
| [28] | Dickey, J. (1973). Scientific reporting and personal probabilities: Student's hypothesis. Journal of the Royal Statistical Society: Series B (Methodological), 35(2), 285-305. https://doi.org/10.1111/j.2517-6161.1973.tb00959.x |
| [29] | Dickey, J. M. (1976). Approximate posterior distributions. Journal of the American Statistical Association, 71(355), 680-689. https://doi.org/10.2307/2285601 |
| [30] | Donkin, C., Heathcote, A., & Brown, S. (2009). Is the linear ballistic accumulator model really the simplest model of choice response times: A Bayesian model complexity analysis. Ninth International Conference on Cognitive Modeling— ICCM2009, Manchester, |
| [31] |
Dorfman, H. M., & Gershman, S. J. (2019). Controllability governs the balance between Pavlovian and instrumental action selection. Nature Communications, 10(1), 5826. https://doi.org/10.1038/s41467-019-13737-7
doi: 10.1038/s41467-019-13737-7 URL pmid: 31862876 |
| [32] | Doucet, A., & Johansen, A. M. (2009). A tutorial on particle filtering and smoothing:Fifteen years later. In Crisan, D. (Ed.), Handbook of nonlinear filtering. Oxford University Press. |
| [33] |
Dziak, J. J., Coffman, D. L., Lanza, S. T., Li, R., & Jermiin, L. S. (2020). Sensitivity and specificity of information criteria. Briefings in Bioinformatics, 21(2), 553-565. https://doi.org/10.1093/bib/bbz016
doi: 10.1093/bib/bbz016 URL pmid: 30895308 |
| [34] | Evans, N. J. (2019). Assessing the practical differences between model selection methods in inferences about choice response time tasks. Psychonomic Bulletin & Review, 26(4), 1070-1098. https://doi.org/10.3758/s13423-018-01563-9 |
| [35] | Evans, N. J., Hawkins, G. E., & Brown, S. D. (2020). The role of passing time in decision-making. Journal of Experimental Psychology: Learning, Memory, and Cognition, 46(2), 316-326. https://doi.org/10.1037/xlm0000725 |
| [36] | Farrell, S., & Lewandowsky, S. (2018). Computational modeling of cognition and behavior. Cambridge University Press. |
| [37] | Fong, E., & Holmes, C. C. (2020). On the marginal likelihood and cross-validation. Biometrika, 107(2), 489-496. https://doi.org/10.1093/biomet/asz077 |
| [38] | Fontanesi, L., Gluth, S., Spektor, M. S., & Rieskamp, J. (2019). A reinforcement learning diffusion decision model for value-based decisions. Psychonomic Bulletin & Review, 26(4), 1099-1121. https://doi.org/10.3758/s13423-018-1554-2 |
| [39] |
Forstmann, B. U., Ratcliff, R., & Wagenmakers, E. J. (2016). Sequential sampling models in cognitive neuroscience: Advantages, applications, and extensions. Annual Review of Psychology, 67, 641-666. https://doi.org/10.1146/annurev-psych-122414-033645
doi: 10.1146/annurev-psych-122414-033645 URL pmid: 26393872 |
| [40] | Friedman, J., Hastie, T., & Tibshirani, R. (2001). The elements of statistical learning. Springer |
| [41] | Friston, K., Kilner, J., & Harrison, L. (2006). A free energy principle for the brain. Journal of Physiology, 100(1-3), 70-87. https://doi.org/10.1016/j.jphysparis.2006.10.001 |
| [42] |
Friston, K., Mattout, J., Trujillo-Barreto, N., Ashburner, J., & Penny, W. (2007). Variational free energy and the Laplace approximation. NeuroImage, 34(1), 220-234. https://doi.org/10.1016/j.neuroimage.2006.08.035
doi: 10.1016/j.neuroimage.2006.08.035 URL pmid: 17055746 |
| [43] | Gamerman, D., & Lopes, H. F. (2006). Markov chain Monte Carlo: Stochastic simulation for Bayesian inference. Chapman & Hall/CRC, Boca Raton, FL. |
| [44] | Geisser, S., & Eddy, W. F. (1979). A predictive approach to model selection. Journal of the American Statistical Association, 74(365), 153-160. https://doi.org/10.1080/01621459.1979.10481632 |
| [45] | Gelfand, A. E., & Dey, D. K. (1994). Bayesian model choice: Asymptotics and exact calculations. Journal of the Royal Statistical Society: Series B (Methodological), 56(3), 501-514. https://doi.org/10.1111/j.2517-6161.1994.tb01996.x |
| [46] | Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). Bayesian data analysis (3rd ed.). Chapman and Hall/CRC. |
| [47] | Gelman, A., Hwang, J., & Vehtari, A. (2013). Understanding predictive information criteria for Bayesian models. Statistics and Computing, 24(6), 997-1016. https://doi.org/10.1007/s11222-013-9416-2 |
| [48] | Geng, H., Chen, J., Hu, C.-P., Jin, J., Chan, R. C. K., Li, Y., ... Zhang, L. (2022). Promoting computational psychiatry in China. Nature Human Behaviour, 6(5), 615-617. https://doi.org/10.1038/s41562-022-01328-4 |
| [49] | Gershman, S. J. (2016). Empirical priors for reinforcement learning models. Journal of Mathematical Psychology, 71, 1-6. https://doi.org/10.1016/j.jmp.2016.01.006 |
| [50] |
Gronau, Q. F., Sarafoglou, A., Matzke, D., Ly, A., Boehm, U., Marsman, M., ... Steingroever, H. (2017). A tutorial on bridge sampling. Journal of Mathematical Psychology, 81, 80-97. https://doi.org/10.1016/j.jmp.2017.09.005
doi: 10.1016/j.jmp.2017.09.005 URL pmid: 29200501 |
| [51] | Gronau, Q. F., & Wagenmakers, E. J. (2019). Limitations of Bayesian Leave-One-Out Cross-Validation for model selection. Computational Brain & Behavior, 2(1), 1-11. https://doi.org/10.1007/s42113-018-0011-7 |
| [52] |
Guitart-Masip, M., Huys, Q. J., Fuentemilla, L., Dayan, P., Duzel, E., & Dolan, R. J. (2012). Go and no-go learning in reward and punishment: Interactions between affect and effect. Neuroimage, 62(1), 154-166. https://doi.org/10.1016/j.neuroimage.2012.04.024
doi: 10.1016/j.neuroimage.2012.04.024 URL pmid: 22548809 |
| [53] | Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2010). Multivariate data analysis (7th ed.). Pearson Prentice Hall. |
| [54] | Hammersley, J. (2013). Monte carlo methods. Springer Science & Business Media. |
| [55] | Heck, D. W. (2019). A caveat on the Savage-Dickey density ratio: The case of computing Bayes factors for regression parameters. British Journal of Mathematical and Statistical Psychology, 72(2), 316-333. https://doi.org/https://doi.org/10.1111/bmsp.12150 |
| [56] |
Hinne, M., Gronau, Q. F., van den Bergh, D., & Wagenmakers, E.-J. (2020). A conceptual introduction to Bayesian model averaging. Advances in Methods and Practices in Psychological Science, 3(2), 200-215. https://doi.org/10.1177/2515245919898657
doi: 10.1177/2515245919898657 URL |
| [57] | Hurvich, C. M., & Tsai, C.-L. (1989). Regression and time series model selection in small samples. Biometrika, 76(2), 297-307. https://doi.org/10.1093/biomet/76.2.297 |
| [58] | Huys, Q. J., Cools, R., Gölzer, M., Friedel, E., Heinz, A., Dolan, R. J., & Dayan, P. (2011). Disentangling the roles of approach, activation and valence in instrumental and pavlovian responding. PLoS Computational Biology, 7(4), e1002028. https://doi.org/10.1371/journal.pcbi.1002028 |
| [59] |
Huys, Q. J., Maia, T. V., & Frank, M. J. (2016). Computational psychiatry as a bridge from neuroscience to clinical applications. Nature Neuroscience, 19(3), 404-413. https://doi.org/10.1038/nn.4238
doi: 10.1038/nn.4238 URL pmid: 26906507 |
| [60] |
Iglesias, S., Mathys, C., Brodersen, K. H., Kasper, L., Piccirelli, M., den Ouden, H. E., & Stephan, K. E. (2013). Hierarchical prediction errors in midbrain and basal forebrain during sensory learning. Neuron, 80(2), 519-530. https://doi.org/10.1016/j.neuron.2013.09.009
doi: 10.1016/j.neuron.2013.09.009 URL pmid: 24139048 |
| [61] |
Ikink, I., Engelmann, J. B., van den Bos, W., Roelofs, K., & Figner, B. (2019). Time ambiguity during intertemporal decision-making is aversive, impacting choice and neural value coding. Neuroimage, 185, 236-244. https://doi.org/10.1016/j.neuroimage.2018.10.008
doi: S1053-8119(18)31967-0 URL pmid: 30296559 |
| [62] | Kass, R. E., & Raftery, A. E. (1995). Bayes factors. Journal of the American Statistical Association, 90(430), 773-795. https://doi.org/10.1080/01621459.1995.10476572 |
| [63] | Körding, K. P., & Wolpert, D. M. (2006). Bayesian decision theory in sensorimotor control. Trends in Cognitive Science, 10(7), 319-326. https://doi.org/10.1016/j.tics.2006.05.003 |
| [64] | Kvålseth, T. O. (1985). Cautionary note about R2. The American Statistician, 39(4), 279-285. https://doi.org/10.1080/00031305.1985.10479448 |
| [65] | Lebreton, M., Bacily, K., Palminteri, S., & Engelmann, J. B. (2019). Contextual influence on confidence judgments in human reinforcement learning. PLoS Computational Biololgy, 15(4), e1006973. https://doi.org/10.1371/journal.pcbi.1006973 |
| [66] |
Li, J., Schiller, D., Schoenbaum, G., Phelps, E. A., & Daw, N. D. (2011). Differential roles of human striatum and amygdala in associative learning. Nature Neuroscience, 14(10), 1250-1252. https://doi.org/10.1038/nn.2904
doi: 10.1038/nn.2904 URL pmid: 21909088 |
| [67] | Li, J. A., Dong, D., Wei, Z., Liu, Y., Pan, Y., Nori, F., & Zhang, X. (2020). Quantum reinforcement learning during human decision-making. Nature Human Behaviour, 4(3), 294-307. https://doi.org/10.1038/s41562-019-0804-2 |
| [68] | Li, Z.-W., & Ma, W. J. (2021). An uncertainty-based model of the effects of fixation on choice. PLOS Computational Biology, 17(8), e1009190. https://doi.org/10.1371/journal.pcbi.1009190 |
| [69] | MacKay, D. J. (2003). Information theory, inference and learning algorithms. Cambridge University Press. |
| [70] | McFadden, D. L. (1984). Chapter 24 Econometric analysis of qualitative response models. In Durlauf, S. N. (Ed.), Handbook of Econometrics (Vol. 2, pp. 1395-1457). Elsevier. https://doi.org/10.1016/S1573-4412(84)02016-X |
| [71] | Menard, S. (2000). Coefficients of determination for multiple logistic regression analysis. The American Statistician, 54(1), 17-24. https://doi.org/10.1080/00031305.2000.10474502 |
| [72] | Meng, X.-L., & Wong, W. H. (1996). Simulating ratios of normalizing constants via a simple identity: A theoretical exploration. Statistica Sinica, 6(4), 831-860. https://www.jstor.org/stable/24306045 |
| [73] | Merlise, C., & Edward, I. G. (2004). Model uncertainty. Statistical Science, 19(1), 81-94. https://doi.org/10.1214/088342304000000035 |
| [74] | Montague, P. R., Dolan, R. J., Friston, K. J., & Dayan, P. (2012). Computational psychiatry. Trends in Cognitive Science, 16(1), 72-80. https://doi.org/10.1016/j.tics.2011.11.018 |
| [75] | Murphy, K. P. (2023). Probabilistic machine learning: An introduction. The MIT Press. |
| [76] | Myung, I. J., & Pitt, M. A. (1997). Applying Occam’s razor in modeling cognition: A Bayesian approach. Psychonomic Bulletin & Review, 4(1), 79-95. https://doi.org/10.3758/BF03210778 |
| [77] | Myung, J., & Pitt, M. (2018). Model comparison in psychology. In Wagenmakers, E.J. (Ed.), Stevens' handbook of experimental psychology and cognitive neuroscience (Vol. 5, pp. 1-34). https://doi.org/10.1002/9781119170174.epcn503 |
| [78] |
Palminteri, S., Wyart, V., & Koechlin, E. (2017). The importance of falsification in computational cognitive modeling. Trends in Cognitive Sciences, 21(6), 425-433. https://doi.org/10.1016/j.tics.2017.03.011
doi: S1364-6613(17)30054-2 URL pmid: 28476348 |
| [79] | Pedersen, M. L., Ironside, M., Amemori, K. I., McGrath, C. L., Kang, M. S., Graybiel, A. M., Pizzagalli, D. A., & Frank, M. J. (2021). Computational phenotyping of brain- behavior dynamics underlying approach-avoidance conflict in major depressive disorder. PLoS Computational Biololgy, 17(5), e1008955. https://doi.org/10.1371/journal.pcbi.1008955 |
| [80] |
Raab, H. A., & Hartley, C. A. (2020). Adolescents exhibit reduced Pavlovian biases on instrumental learning. Scientific reports, 10(1), 15770. https://doi.org/10.1038/s41598-020-72628-w
doi: 10.1038/s41598-020-72628-w URL pmid: 32978451 |
| [81] |
Ratcliff, R., Smith, P. L., Brown, S. D., & McKoon, G. (2016). Diffusion decision model: Current issues and history. Trends in Cognitive Sciences, 20(4), 260-281. https://doi.org/10.1016/j.tics.2016.01.007
doi: S1364-6613(16)00025-5 URL pmid: 26952739 |
| [82] |
Schultz, W., Dayan, P., & Montague, P. R. (1997). A neural substrate of prediction and reward. Science, 275(5306), 1593. https://doi.org/10.1126/science.275.5306.1593
doi: 10.1126/science.275.5306.1593 URL pmid: 9054347 |
| [83] | Schwarz, G. (1978). Estimating the dimension of a model. The Annals of Statistics, 6(2), 461-464. https://www.jstor.org/stable/2958889 |
| [84] | Sclove, S. L. (1987). Application of model-selection criteria to some problems in multivariate analysis. Psychometrika, 52(3), 333-343. https://doi.org/10.1007/BF02294360 |
| [85] | Sivula, T., Magnusson, M., Matamoros, A. A., & Vehtari, A. (2020). Uncertainty in Bayesian leave-one-out cross- validation based model comparison. arXiv. https://doi.org/10.48550/arXiv.2001.00980 |
| [86] | Spiegelhalter, D. J., Best, N. G., Carlin, B. P., & Van Der Linde, A. (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64(4), 583-639. https://doi.org/10.1111/1467-9868.00353 |
| [87] | Spiegelhalter, D. J., Best, N. G., Carlin, B. P., & Van Der Linde, A. (2014). The deviance information criterion: 12 years on. Journal of the Royal Statistical Society. Series B (Statistical Methodology), 76(3), 485-493. http://www.jstor.org/stable/24774528 |
| [88] |
Steinberg, E. E., Keiflin, R., Boivin, J. R., Witten, I. B., Deisseroth, K., & Janak, P. H. (2013). A causal link between prediction errors, dopamine neurons and learning. Nature Neuroscience, 16(7), 966-973. https://doi.org/10.1038/nn.3413
doi: 10.1038/nn.3413 URL pmid: 23708143 |
| [89] | Steingroever, H., Wetzels, R., & Wagenmakers, E.-J. (2014). Absolute performance of reinforcement-learning models for the Iowa Gambling Task. Decision, 1(3), 161-183. https://doi.org/10.1037/dec0000005 |
| [90] | Steingroever, H., Wetzels, R., & Wagenmakers, E.-J. (2016). Bayes factors for reinforcement-learning models of the Iowa gambling task. Decision, 3(2), 115-131. https://doi.org/10.1037/dec0000040 |
| [91] |
Stephan, K. E., Penny, W. D., Daunizeau, J., Moran, R. J., & Friston, K. J. (2009). Bayesian model selection for group studies. Neuroimage, 46(4), 1004-1017. https://doi.org/10.1016/j.neuroimage.2009.03.025
doi: 10.1016/j.neuroimage.2009.03.025 URL pmid: 19306932 |
| [92] | Stone, M. (1977). An asymptotic equivalence of choice of model by cross-validation and Akaike's criterion. Journal of the Royal Statistical Society: Series B, 39(1), 44-47. https://doi.org/10.1111/j.2517-6161.1977.tb01603.x |
| [93] | Sugiura, N. (1978). Further analysis of the data by akaike's information criterion and the finite corrections: Further analysis of the data by akaike's. Communications in Statistics-theory Methods, 7(1), 13-26. https://doi.org/10.1080/03610927808827599 |
| [94] |
Suzuki, S., Harasawa, N., Ueno, K., Gardner, J. L., Ichinohe, N., Haruno, M., Cheng, K., & Nakahara, H. (2012). Learning to simulate others' decisions. Neuron, 74(6), 1125-1137. https://doi.org/10.1016/j.neuron.2012.04.030
doi: 10.1016/j.neuron.2012.04.030 URL pmid: 22726841 |
| [95] | Swart, J. C., Fröbose, M. I., Cook, J. L., Geurts, D. E., Frank, M. J., Cools, R., & den Ouden, H. E. (2017). Catecholaminergic challenge uncovers distinct Pavlovian and instrumental mechanisms of motivated (in)action. Elife, 6. https://doi.org/10.7554/eLife.22169 |
| [96] | Vandekerckhove, J., Matzke, D., & Wagenmakers, E.-J. (2015). Model comparison and the principle of parsimony. In Busemeyer, J. R., Wang, Z., Townsend, J. T., & Eidels, A. (Eds.), The Oxford handbook of computational and mathematical psychology. (pp.300-319). Oxford University Press. |
| [97] |
Vandekerckhove, J., Tuerlinckx, F., & Lee, M. D. (2011). Hierarchical diffusion models for two-choice response times. Psychological Methods, 16(1), 44-62. https://doi.org/10.1037/a0021765
doi: 10.1037/a0021765 URL pmid: 21299302 |
| [98] | van de Schoot, R., Depaoli, S., King, R., Kramer, B., Märtens, K., Tadesse, M. G., ... Yau, C. (2021). Bayesian statistics and modelling. Nature Reviews Methods Primers, 1(1), 1-26. https://doi.org/10.1038/s43586-021-00017-2 |
| [99] | Vehtari, A. (2022). Cross-validation FAQ. https://avehtari.github.io/modelselection/CV-FAQ.html |
| [100] | Vehtari, A., Gelman, A., & Gabry, J. (2017). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing, 27(5), 1413-1432. https://doi.org/10.1007/s11222-016-9696-4 |
| [101] | Vehtari, A., Mononen, T., Tolvanen, V., Sivula, T., & Winther, O. (2016). Bayesian leave-one-out cross-validation approximations for Gaussian latent variable models. The Journal of Machine Learning Research, 17(1), 3581-3618. http://jmlr.org/papers/v17/14-540.html |
| [102] | Vehtari, A., Simpson, D. P., Yao, Y., & Gelman, A. (2019). Limitations of “Limitations of Bayesian Leave-one-out Cross-Validation for Model Selection”. Computational Brain & Behavior, 2(1), 22-27. https://doi.org/10.1007/s42113-018-0020-6 |
| [103] |
Verstynen, T., & Kording, K. P. (2023). Overfitting to ‘predict’ suicidal ideation. Nature Human Behaviour, 7(5), 680-681. https://doi.org/10.1038/s41562-023-01560-6
doi: 10.1038/s41562-023-01560-6 URL pmid: 37024723 |
| [104] |
Vrieze, S. I. (2012). Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychological Methods, 17(2), 228-243. https://doi.org/10.1037/a0027127
doi: 10.1037/a0027127 URL pmid: 22309957 |
| [105] | Wagenmakers, E.-J., & Farrell, S. (2004). AIC model selection using Akaike weights. Psychonomic Bulletin & Review, 11(1), 192-196. https://doi.org/10.3758/BF03206482 |
| [106] |
Wagenmakers, E. J., Lodewyckx, T., Kuriyal, H., & Grasman, R. (2010). Bayesian hypothesis testing for psychologists: A tutorial on the Savage-Dickey method. Cognitive Psychology, 60(3), 158-189. https://doi.org/10.1016/j.cogpsych.2009.12.001
doi: 10.1016/j.cogpsych.2009.12.001 URL pmid: 20064637 |
| [107] | Wasserman, L. (2006). All of nonparametric statistics. Springer Science & Business Media. |
| [108] | Watanabe, S. (2010). Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. Journal of Machine Learning Research, 11(12). http://jmlr.org/papers/v11/watanabe10a.html |
| [109] |
Westbrook, A., van den Bosch, R., Määttä, J., Hofmans, L., Papadopetraki, D., Cools, R., & Frank, M. J. (2020). Dopamine promotes cognitive effort by biasing the benefits versus costs of cognitive work. Science, 367(6484), 1362-1366. https://doi.org/10.1126/science.aaz5891
doi: 10.1126/science.aaz5891 URL pmid: 32193325 |
| [110] | Wilks, S. S. (1938). The large-sample distribution of the likelihood ratio for testing composite hypotheses. The Annals of Mathematical Statistics, 9(1), 60-62. http://www.jstor.org/stable/2957648 |
| [111] | Wilson, R. C., & Collins, A. G. (2019). Ten simple rules for the computational modeling of behavioral data. Elife, 8. https://doi.org/10.7554/eLife.49547 |
| [112] | Yang, Y. (2005). Can the strengths of AIC and BIC be shared? A conflict between model indentification and regression estimation. Biometrika, 92(4), 937-950. https://doi.org/10.1093/biomet/92.4.937 |
| [113] | Yao, Y., Vehtari, A., Simpson, D., & Gelman, A. (2018). Using stacking to average Bayesian predictive distributions (with discussion). Bayesian Analysis, 13(3), 917-1007. https://doi.org/10.1214/17-BA1091 |
| [114] |
Zhang, L., Lengersdorff, L., Mikus, N., Gläscher, J., & Lamm, C. (2020). Using reinforcement learning models in social neuroscience: Frameworks, pitfalls and suggestions of best practices. Social Cognitive and Affective Neuroscience, 15(6), 695-707. https://doi.org/10.1093/scan/nsaa089
doi: 10.1093/scan/nsaa089 URL pmid: 32608484 |
| [115] | Zhang, Y., & Yang, Y. (2015). Cross-validation for selecting a model selection procedure. Journal of Econometrics, 187(1), 95-112. https://doi.org/10.1016/j.jeconom.2015.02.006 |
| [1] | 温秀娟, 马毓璟, 谭斯祺, 李芸, 刘文华. 身体还是认知努力的损害?抑郁症努力奖赏动机评估及计算模型应用[J]. 心理科学进展, 2025, 33(1): 107-122. |
| [2] | 李兴珊, 张淇玮, 黄林洁琼. 中文词汇语义加工过程的计算模拟与实验验证[J]. 心理科学进展, 2024, 32(9): 1379-1392. |
| [3] | 韩宜瑾, 朱金丽, 侯方. 弱视视觉系统的对比度增益研究[J]. 心理科学进展, 2023, 31(suppl.): 4-4. |
| [4] | 黎穗卿, 陈新玲, 翟瑜竹, 张怡洁, 章植鑫, 封春亮. 人际互动中社会学习的计算神经机制[J]. 心理科学进展, 2021, 29(4): 677-696. |
| [5] | 高青林, 周媛. 计算模型视角下信任形成的心理和神经机制——基于信任博弈中投资者的角度[J]. 心理科学进展, 2021, 29(1): 178-189. |
| [6] | 张银花, 李红, 吴寅. 计算模型在道德认知研究中的应用[J]. 心理科学进展, 2020, 28(7): 1042-1055. |
| [7] | 李精精, 张剑, 田慧荣, Jeffrey B.Vancouver. 动态计算模型在组织行为学研究中的应用[J]. 心理科学进展, 2020, 28(2): 368-380. |
| [8] | 区健新, 吴寅, 刘金婷, 李红. 计算精神病学:抑郁症研究和临床应用的新视角[J]. 心理科学进展, 2020, 28(1): 111-127. |
| [9] | 高绍兵, 李永杰. 结合视觉自底向上和自顶向下机制的多光源颜色恒常性算法研究[J]. 心理科学进展, 2019, 27(suppl.): 96-96. |
| [10] | 任衍具;傅小兰. 图表加工的理论模型[J]. 心理科学进展, 2006, 14(1): 23-31. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||