问题解决任务中行动序列的二分类建模：单/两参数行动序列模型

doi:10.3724/SP.J.1041.2023.01383

摘要/Abstract

摘要：

行动序列作为一种典型的过程数据, 可反映被试解决问题的详细步骤。鉴于行动或状态转移可区分正误, 本文基于二分类Logistic建模提出两个复杂度相对较低的行动序列模型——单/两参数行动序列模型(1P-/2P-ASM); 两者差异在于是否允许自由估计问题状态的区分度。通过实证研究和模拟研究对比探究两个新模型与基于多分类Logistic建模的序列作答模型(SRM)的表现。研究结果主要发现：(1)两个ASM能够获得与SRM几乎一致的问题解决能力估计值; (2)两个ASM的计算耗时明显低于SRM的; (3) 2P-ASM比1P-ASM的综合表现更优。总之, 两个模型复杂度相对低的ASM均能够实现对行动序列的有效分析, 有益于行动序列数据分析的落地。

关键词: 过程数据, 行动序列, 问题状态转换, 行动序列模型, 项目反应理论

Abstract:

Process data refers to the human-computer or human-human interaction data recorded in computerized learning and assessment systems that reflect respondents’ problem-solving processes. Among the process data, action sequences are the most typical data because they reflect how respondents solve the problem step by step. However, the non-standardized format of action sequences (i.e., different data lengths for different participants) also poses difficulties for the direct application of traditional psychometric models. Han et al. (2021) proposed the SRM by combining dynamic Bayesian networks with the nominal response model (NRM) to address the shortcomings of existing methods. Similar to the NRM, the SRM uses multinomial logistic modeling, which in turn assigns different parameters to each possible action or state transition in the task, leading to high model complexity. Given that actions or state transitions in problem-solving tasks have correct and incorrect outcomes rather than equivalence relations without quantitative order, this paper proposes two action sequence models based on binary logistic modeling with relatively low model complexity: the one- and two-parameter action sequence models (1P and 2P-ASM). Unlike the SRM, which applies the NRM migration to action sequence analysis, the 1P-ASM and 2P-ASM migrate the simpler one- and two-parameter IRT models to action sequence analysis, respectively.

An illustrated example was provided to compare the performance of SRM and two ASMs with a real-world interactive assessment item, “Tickets,” in the PISA 2012. The results mainly showed that: (1) the latent ability estimates of two ASMs and the SRM had high correlation; (2) ASMs took less computing time than that of SRM; (3) participants who are solving the problem correctly tend to continue to present the correct actions, and vice versa; and (4) compared with the fixed discrimination parameter of the SRM, the free estimated discrimination parameter of the 2P-ASM helped us to better understand the task.

A simulation study was further designed to explore the psychometric performance of the proposed model in different test scenarios. Two factors were manipulated: sample size (including 100, 200, and 500) and average problem state transition sequence length (including short and long). The SRM was used to generate the state transition sequences in the simulation study. The problem-solving task structure from the empirical study was used. The results showed that: (1) two ASMs could provide accurate parameter estimates even if they were not the data-generation model; (2) the computation time of both ASMs was lower than that of SRM, especially under the condition of a small sample size; (3) the problem-solving ability estimates of both ASMs were in high agreement with the problem-solving ability estimate of the SRM, and the agreement between 2P-ASM and SRM is relatively higher; and (4) the longer the problem state transition sequence, the better the recovery of problem-solving ability parameter for both ASMs and SRM.

Overall, the two ASMs proposed in this paper based on binary logistic modeling can achieve effective analysis of action sequences and provide almost identical estimates of participants' problem-solving ability to SRM while significantly reducing the computational time. Meanwhile, combining the results of simulation and empirical studies, we believe that the 2P-ASM has better overall performance than the 1P-ASM; however, the more parsimonious 1P-ASM is recommended when the sample size is small (e.g., 100 participants) or the task is simple (fewer operations are required to solve the problem).

Key words: process data, action sequence, problem state transition, action sequence model, item response theory

中图分类号:

B841

付颜斌, 陈琦鹏, 詹沛达. (2023). 问题解决任务中行动序列的二分类建模：单/两参数行动序列模型. 心理学报, 55(8), 1383-1396.

FU Yanbin, CHEN Qipeng, ZHAN Peida. (2023). Binary modeling of action sequences in problem-solving tasks: One- and two-parameter action sequence model. Acta Psychologica Sinica, 55(8), 1383-1396.

图/表 30

图1 问题解决任务示意图注：红色实线箭头表示正确状态转移, 黑色虚线箭头表示错误状态转移; S→A→C→E为最优行动序列, 其中包含S→A、A→C和C→E三个状态转移。省略号表示问题解决流程的重复出现。

图2 序列作答模型示意图注：θn为被试n的问题解决能力; S n 1为学生 n在阶段1所处的问题状态, 依此类推; S n 1 → S n 2为学生 n从阶段1向阶段2转移的状态转移, 依此类推。

图3 问题解决任务二分编码示意图注：红色实线箭头表示正确状态转移, 编码为1; 黑色虚线箭头表示错误状态转移, 编码为0; 省略号表示问题解决流程的重复出现。

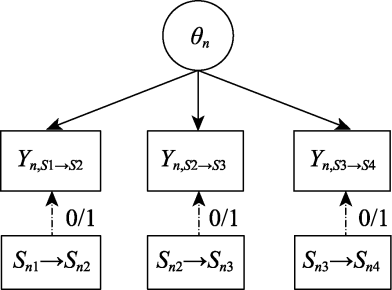
图4 二分类行动序列模型建模示意图注：θn为被试n的问题解决能力; Sn1为学生 n在阶段1所处的问题状态, 依此类推; Sn1 → Sn2为学生 n从阶段1向阶段2转移的状态转移, 依此类推; Yn,S1→S2为二分编码后的状态转移, Yn,S1→S2 = 1表示被试n呈现了正确状态转移, Yn,S1→S2 = 0表示被试n呈现了错误状态转移; 不同学生的行动序列长度不同, 方框数不同。

图5 PISA 2012购票任务初始界面

图6 PISA 2012购票任务结构图

表1 PISA 2012购票任务所类比的“选择题”

当前问题状态	下一阶段可选问题状态(转移选项)
S	A (1)	F (0)
A	B (1)	G (0)	S (0)
B	C (1)	H (0)	S (0)
C	D (1)	E (0)	S (0)	J (0)
D	J (1)	E (0)	S (0)
E	D (1)	J (0)	S (0)
F	S (1)	G (0)
G	S (1)	H (0)
H	S (1)	I (0)	J (0)
I	S (1)	J (0)

表2 实证研究中三个模型对数据的拟合情况和计算耗时

模型	LOO	WAIC	ppp	计算时间(秒)
1P-ASM	11018.208	11007.133	0.511	647.5
2P-ASM	10363.785	10275.475	0.518	958.5
SRM	16804.501	16803.925	0.498	1958.6

表3 实证研究中行动序列模型参数估计结果

当前问题状态	1P-ASM			2P-ASM
	容易度			容易度			区分度
	后验均值	后验标准差	95% HPD	后验均值	后验标准差	95% HPD	后验均值	后验标准差	95% HPD
S	0.911	0.046	(0.822, 1.001)	0.969	0.057	(0.860, 1.084)	1.343	0.116	(1.111, 1.570)
A	1.553	0.066	(1.425, 1.682)	1.547	0.077	(1.401, 1.701)	1.457	0.212	(1.043, 1.870)
B	1.432	0.073	(1.290, 1.577)	1.354	0.082	(1.198, 1.521)	1.797	0.398	(0.958, 2.566)
C	1.436	0.080	(1.279, 1.599)	1.207	0.148	(0.940, 1.526)	3.015	0.885	(1.104, 4.759)
E	2.008	0.107	(1.801, 2.215)	1.734	0.159	(1.456, 2.099)	1.615	0.495	(0.463, 2.576)
D	0.361	0.176	(0.015, 0.702)	0.472	0.283	(−0.031, 1.064)	1.472	0.952	(0.225, 3.792)
F	−1.705	0.107	(−1.918, −1.492)	−1.590	0.123	(−1.829, −1.348)	1.438	0.250	(0.982, 1.974)
G	−1.888	0.111	(−2.105, −1.677)	−1.747	0.147	(−2.050, −1.480)	2.115	0.354	(1.495, 2.875)
H	−0.749	0.075	(−0.898, −0.599)	−0.292	0.172	(−0.636, 0.037)	2.229	0.426	(1.400, 3.088)
I	−0.368	0.157	(−0.686, 0.062)	0.760	0.470	(−0.101, 1.753)	3.127	0.933	(1.525, 5.179)

图7 实证数据中三个模型的问题解决能力参数后验均值对比散点图及概率密度图注: 1P-ASM = 单参数行动序列模型; 2P-ASM = 两参数行动序列模型; SRM = 序列作答模型; r = 皮尔逊积差相关。

表4 典型行动序列对应的问题解决能力估计值的描述统计

问题状态转移序列	频数	SRM			1P-ASM			2P-ASM
问题状态转移序列	频数	均值	中位数	标准差	均值	中位数	标准差	均值	中位数	标准差
SABCDJ	737	0.837	0.837	0.011	0.821	0.821	0.009	0.666	0.665	0.012
SFSABCDJ	35	0.525	0.525	0.007	0.676	0.677	0.007	0.604	0.603	0.010
SFGSABCDJ	22	0.345	0.347	0.007	0.598	0.598	0.005	0.488	0.487	0.009
SABCEDJ	23	0.279	0.279	0.007	−0.017	−0.018	0.005	0.257	0.258	0.008
SFGHSABCDJ	52	0.152	0.151	0.006	0.304	0.304	0.004	0.295	0.296	0.009
SABCJ	47	0.023	0.025	0.007	−0.238	−0.237	0.006	−0.035	−0.035	0.011
SABCEJ	27	−0.250	−0.250	0.005	−0.404	−0.404	0.005	−0.338	−0.338	0.012
SABHJ	117	−0.364	−0.364	0.007	−0.506	−0.506	0.006	−0.359	−0.358	0.010
SAGHJ	65	−0.662	−0.662	0.008	−0.741	−0.742	0.008	−0.594	−0.594	0.010
SAGHIJ	45	−0.806	−0.806	0.008	−0.940	−0.939	0.007	−0.760	−0.760	0.010
SFGHJ	337	−1.099	−1.099	0.011	−1.033	−1.033	0.008	−0.869	−0.869	0.011
SFGHIJ	95	−1.228	−1.227	0.011	−1.201	−1.201	0.008	−1.020	−1.021	0.010

表5 模拟研究中三个模型的问题解决能力参数的估计返真性和计算耗时

样本量	序列长度	模型	均Bias	均RMSE	Cor	ART(秒)
100	短	1P-ASM	−0.002	0.534	0.854	18.117
		2P-ASM	−0.002	0.534	0.852	30.274
		SRM	0.007	0.515	0.863	1029.189
	长	1P-ASM	−0.011	0.441	0.910	24.393
		2P-ASM	−0.011	0.408	0.917	37.100
		SRM	−0.026	0.395	0.921	1321.361
200	短	1P-ASM	0.007	0.523	0.855	41.923
		2P-ASM	0.007	0.518	0.858	66.395
		SRM	0.011	0.507	0.864	527.740
	长	1P-ASM	0.010	0.438	0.912	54.448
		2P-ASM	0.010	0.395	0.921	76.707
		SRM	0.002	0.386	0.924	691.308
500	短	1P-ASM	−0.004	0.516	0.856	119.439
		2P-ASM	−0.004	0.504	0.863	198.838
		SRM	−0.001	0.500	0.865	590.051
	长	1P-ASM	0.005	0.444	0.907	160.661
		2P-ASM	0.005	0.394	0.920	236.195
		SRM	0.002	0.391	0.921	801.767

表6 模拟研究中两个ASM和SRM的问题解决能力参数估计的一致性

样本量	序列长度	1P-ASM与SRM			2P-ASM与SRM
样本量	序列长度	均CBias	均CRMSE	Ccor	均Cbias	均CRMSE	Ccor
100	短	−0.009	0.126	0.991	−0.009	0.129	0.989
100	长	0.015	0.200	0.986	0.015	0.098	0.995
200	短	−0.004	0.126	0.991	−0.004	0.098	0.994
200	长	0.008	0.208	0.986	0.008	0.077	0.997
500	短	−0.002	0.126	0.990	−0.002	0.060	0.998
500	长	0.003	0.211	0.986	0.003	0.042	0.999

表A1 三种行动序列数据分析模型的对比

模型	正确状态转移	错误状态转移
模型	1	2	3	…	K
序列作答模型	P₁	P₂	P₃	…	P_K
状态作答模型	P₁	$(1 − P 1) / (K − 1)$	$(1 − P 1) / (K − 1)$		$(1 − P 1) / (K − 1)$
行动序列模型	P₁	$1 − P 1$

表A1 三种行动序列数据分析模型的对比

模型	正确状态转移	错误状态转移
模型	1	2	3	…	K
序列作答模型	P₁	P₂	P₃	…	P_K
状态作答模型	P₁	$(1 − P 1) / (K − 1)$	$(1 − P 1) / (K − 1)$		$(1 − P 1) / (K − 1)$
行动序列模型	P₁	$1 − P 1$

图A1 PISA 2012 Tickets购票任务截图

图A2 CP038Q02购票任务问题解决流程注：红色箭头表示了完美解决该问题的步骤。

表A2 异常行动序列示例

Cnt	SchoolID	StdID	Event	Time	Event Number	Action
ARE	0000068	01770	START_ITEM	843.1000	1.00	NULL
ARE	0000068	01770	ACER_EVENT	885.2000	2.00	country_trains
ARE	0000068	01770	ACER_EVENT	892.3000	3.00	full_fare
ARE	0000068	01770	ACER_EVENT	894.1000	4.00	daily
ARE	0000068	01770	ACER_EVENT	904.5000	5.00	Cancel
ARE	0000068	01770	ACER_EVENT	914.7000	6.00	country_trains
ARE	0000068	01770	ACER_EVENT	915.0000	7.00	full_fare
ARE	0000068	01770	ACER_EVENT	915.9000	8.00	individual
ARE	0000068	01770	ACER_EVENT	917.5000	9.00	trip_2
ARE	0000068	01770	ACER_EVENT	923.0000	10.00	Buy
ARE	0000068	01770	END_ITEM	928.5000	11.00	NULL
ARE	0000068	01770	END_ITEM	928.5000	12.00	NULL
ARE	0000068	01770	ACER_EVENT	923.0000	13.00	Buy
ARE	0000068	01770	ACER_EVENT	917.5000	14.00	trip_2
ARE	0000068	01770	ACER_EVENT	915.9000	15.00	individual
ARE	0000068	01770	ACER_EVENT	915.0000	16.00	full_fare
ARE	0000068	01770	ACER_EVENT	914.7000	17.00	country_trains
ARE	0000068	01770	ACER_EVENT	904.5000	18.00	Cancel
ARE	0000068	01770	ACER_EVENT	894.1000	19.00	daily
ARE	0000068	01770	ACER_EVENT	892.3000	20.00	full_fare
ARE	0000068	01770	ACER_EVENT	885.2000	21.00	country_trains

表A3 ppp值计算逻辑

模型		统计量
SRM	观测值	$O (S; λ ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 S n, p → S n, p + 1$
SRM	抽样值	$O (S r e p'; λ ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 S n, p r e p' → S n, p + 1 r e p'$
1P-ASM	观测值	$O (Y; β ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 Y n, S p → S p + 1$
1P-ASM	抽样值	$O (Y r e p'; β ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 Y n, S p → S p + 1 r e p ′$
2P-ASM	观测值	$O (Y; β ′, γ ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 Y n, S p → S p + 1$
2P-ASM	抽样值	$O (Y r e p'; β ′, γ ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 Y n, S p → S p + 1 r e p ′$

表A3 ppp值计算逻辑

模型		统计量
SRM	观测值	$O (S; λ ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 S n, p → S n, p + 1$
SRM	抽样值	$O (S r e p'; λ ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 S n, p r e p' → S n, p + 1 r e p'$
1P-ASM	观测值	$O (Y; β ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 Y n, S p → S p + 1$
1P-ASM	抽样值	$O (Y r e p'; β ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 Y n, S p → S p + 1 r e p ′$
2P-ASM	观测值	$O (Y; β ′, γ ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 Y n, S p → S p + 1$
2P-ASM	抽样值	$O (Y r e p'; β ′, γ ′, θ ′) = ∑ n = 1 N ∑ p = 1 P n − 1 Y n, S p → S p + 1 r e p ′$

图A3 1P-ASM截距参数的轨迹图

图A4 1P-ASM截距参数的后验分布图

图A5 2P-ASM截距参数的轨迹图

图A6 2P-ASM截距参数的后验分布图

图A7 SRM状态转移倾向参数的轨迹图

图A8 SRM状态转移倾向参数的后验分布图

表A4 模拟研究中状态转移倾向参数的真值

状态转移倾向参数	短序列	长序列	状态转移倾向参数	短序列	长序列	状态转移倾向参数	短序列	长序列
$λ S A$	0.496	0.410	$λ C E$	0.472	0.585	$λ F S$	−1.001	0.965
$λ S F$	−0.469	−0.459	$λ C S$	0.451	0.809	$λ F G$	1.013	−1.004
$λ A B$	1.468	1.503	$λ C J$	0.094	0.115	$λ G S$	−0.481	0.522
$λ A G$	−0.375	−1.096	$λ D J$	−0.993	−1.023	$λ G H$	0.432	−0.599
$λ A S$	−1.091	−0.456	$λ D E$	0.362	0.390	$λ H S$	−0.171	0.223
$λ B C$	0.381	−0.932	$λ D S$	0.595	0.678	$λ H I$	0.171	−0.134
$λ B H$	−0.146	0.240	$λ E D$	0.184	0.090	$λ H J$	0.028	−0.114
$λ B S$	−0.273	0.758	$λ E J$	−0.217	−0.227	$λ I S$	−0.159	0.431
$λ C D$	−1.001	−1.481	$λ E S$	0.185	0.149	$λ I J$	0.071	−0.412

表A4 模拟研究中状态转移倾向参数的真值

状态转移倾向参数	短序列	长序列	状态转移倾向参数	短序列	长序列	状态转移倾向参数	短序列	长序列
$λ S A$	0.496	0.410	$λ C E$	0.472	0.585	$λ F S$	−1.001	0.965
$λ S F$	−0.469	−0.459	$λ C S$	0.451	0.809	$λ F G$	1.013	−1.004
$λ A B$	1.468	1.503	$λ C J$	0.094	0.115	$λ G S$	−0.481	0.522
$λ A G$	−0.375	−1.096	$λ D J$	−0.993	−1.023	$λ G H$	0.432	−0.599
$λ A S$	−1.091	−0.456	$λ D E$	0.362	0.390	$λ H S$	−0.171	0.223
$λ B C$	0.381	−0.932	$λ D S$	0.595	0.678	$λ H I$	0.171	−0.134
$λ B H$	−0.146	0.240	$λ E D$	0.184	0.090	$λ H J$	0.028	−0.114
$λ B S$	−0.273	0.758	$λ E J$	−0.217	−0.227	$λ I S$	−0.159	0.431
$λ C D$	−1.001	−1.481	$λ E S$	0.185	0.149	$λ I J$	0.071	−0.412

表A5 模拟研究中1P-ASM截距参数在不同信息水平下的估计结果

截距	有信息先验			无信息先验
截距	均值	标准差	95%HPD	均值	标准差	95%HPD
$β S$	0.941	0.050	(0.844, 1.038)	0.947	0.049	(0.852, 1.042)
$β A$	1.613	0.068	(1.484, 1.751)	1.623	0.069	(1.492, 1.758)
$β B$	−1.595	0.063	(−1.720, −1.470)	−1.603	0.062	(−1.725, −1.480)
$β C$	−2.383	0.117	(−2.618, −2.161)	−2.421	0.118	(−2.650, −2.195)
$β D$	−1.344	0.140	(−1.614, −1.061)	−1.377	0.143	(−1.660, −1.094)
$β E$	0.069	0.168	(−0.256, 0.396)	0.070	0.170	(−0.264, 0.404)
$β F$	1.801	0.087	(1.632, 1.978)	1.820	0.086	(1.654, 1.982)
$β G$	0.560	0.115	(0.332, 0.782)	0.573	0.122	(0.328, 0.809)
$β H$	−0.214	0.087	(−0.385, −0.040)	−0.212	0.087	(−0.385, −0.038)
$β I$	0.839	0.154	(0.547, 1.139)	0.867	0.154	(0.567, 1.166)

表A5 模拟研究中1P-ASM截距参数在不同信息水平下的估计结果

截距	有信息先验			无信息先验
截距	均值	标准差	95%HPD	均值	标准差	95%HPD
$β S$	0.941	0.050	(0.844, 1.038)	0.947	0.049	(0.852, 1.042)
$β A$	1.613	0.068	(1.484, 1.751)	1.623	0.069	(1.492, 1.758)
$β B$	−1.595	0.063	(−1.720, −1.470)	−1.603	0.062	(−1.725, −1.480)
$β C$	−2.383	0.117	(−2.618, −2.161)	−2.421	0.118	(−2.650, −2.195)
$β D$	−1.344	0.140	(−1.614, −1.061)	−1.377	0.143	(−1.660, −1.094)
$β E$	0.069	0.168	(−0.256, 0.396)	0.070	0.170	(−0.264, 0.404)
$β F$	1.801	0.087	(1.632, 1.978)	1.820	0.086	(1.654, 1.982)
$β G$	0.560	0.115	(0.332, 0.782)	0.573	0.122	(0.328, 0.809)
$β H$	−0.214	0.087	(−0.385, −0.040)	−0.212	0.087	(−0.385, −0.038)
$β I$	0.839	0.154	(0.547, 1.139)	0.867	0.154	(0.567, 1.166)

表A6 模拟研究中2P-ASM截距参数在不同信息水平下的估计结果

截距	有信息先验			无信息先验
截距	均值	标准差	95%HPD	均值	标准差	95%HPD
$β S$	1.061	0.064	(0.937, 1.187)	1.069	0.068	(0.937, 1.210)
$β A$	1.679	0.084	(1.517, 1.844)	1.694	0.086	(1.529, 1.864)
$β B$	−1.910	0.109	(−2.125, −1.699)	−1.933	0.113	(−2.167, −1.723)
$β C$	−2.581	0.310	(−3.220, −2.004)	−2.876	0.375	(−3.665, −2.197)
$β D$	−1.026	0.305	(−1.651, −0.463)	−0.987	0.531	(−1.900, −0.005)
$β E$	−0.135	0.291	(−0.719, 0.413)	−0.169	0.331	(−0.863, 0.454)
$β F$	2.212	0.168	(1.904, 2.554)	2.288	0.174	(1.967, 2.643)
$β G$	1.247	0.247	(0.780, 1.750)	1.374	0.268	(0.896, 1.936)
$β H$	−0.139	0.104	(−0.341, 0.064)	−0.130	0.108	(−0.338, 0.078)
$β I$	1.238	0.250	(0.772, 1.745)	1.356	0.275	(0.860, 1.933)

表A6 模拟研究中2P-ASM截距参数在不同信息水平下的估计结果

截距	有信息先验			无信息先验
截距	均值	标准差	95%HPD	均值	标准差	95%HPD
$β S$	1.061	0.064	(0.937, 1.187)	1.069	0.068	(0.937, 1.210)
$β A$	1.679	0.084	(1.517, 1.844)	1.694	0.086	(1.529, 1.864)
$β B$	−1.910	0.109	(−2.125, −1.699)	−1.933	0.113	(−2.167, −1.723)
$β C$	−2.581	0.310	(−3.220, −2.004)	−2.876	0.375	(−3.665, −2.197)
$β D$	−1.026	0.305	(−1.651, −0.463)	−0.987	0.531	(−1.900, −0.005)
$β E$	−0.135	0.291	(−0.719, 0.413)	−0.169	0.331	(−0.863, 0.454)
$β F$	2.212	0.168	(1.904, 2.554)	2.288	0.174	(1.967, 2.643)
$β G$	1.247	0.247	(0.780, 1.750)	1.374	0.268	(0.896, 1.936)
$β H$	−0.139	0.104	(−0.341, 0.064)	−0.130	0.108	(−0.338, 0.078)
$β I$	1.238	0.250	(0.772, 1.745)	1.356	0.275	(0.860, 1.933)

表A7 模拟研究中2P-ASM斜率参数在不同信息水平下的估计结果

斜率	有信息先验			无信息先验
斜率	均值	标准差	95%HPD	均值	标准差	95%HPD
$γ S$	2.165	0.145	(1.902, 2.463)	2.185	0.149	(1.908, 2.498)
$γ A$	2.268	0.208	(1.885, 2.703)	2.308	0.213	(1.909, 2.753)
$γ B$	2.075	0.186	(1.736, 2.459)	2.121	0.193	(1.760, 2.510)
$γ C$	1.499	0.315	(0.921, 2.162)	1.772	0.374	(1.102, 2.560)
$γ D$	0.913	0.298	(0.382, 1.537)	0.858	0.535	(0.000, 1.764)
$γ E$	1.722	0.494	(0.823, 2.764)	1.810	0.562	(0.829, 3.024)
$γ F$	2.125	0.246	(1.655, 2.624)	2.238	0.254	(1.770, 2.758)
$γ G$	2.567	0.390	(1.866, 3.379)	2.764	0.431	(1.978, 3.695)
$γ H$	2.663	0.282	(2.151, 3.254)	2.699	0.287	(2.190, 3.310)
$γ I$	2.188	0.418	(1.419, 3.045)	2.383	0.466	(1.559, 3.387)

表A7 模拟研究中2P-ASM斜率参数在不同信息水平下的估计结果

斜率	有信息先验			无信息先验
斜率	均值	标准差	95%HPD	均值	标准差	95%HPD
$γ S$	2.165	0.145	(1.902, 2.463)	2.185	0.149	(1.908, 2.498)
$γ A$	2.268	0.208	(1.885, 2.703)	2.308	0.213	(1.909, 2.753)
$γ B$	2.075	0.186	(1.736, 2.459)	2.121	0.193	(1.760, 2.510)
$γ C$	1.499	0.315	(0.921, 2.162)	1.772	0.374	(1.102, 2.560)
$γ D$	0.913	0.298	(0.382, 1.537)	0.858	0.535	(0.000, 1.764)
$γ E$	1.722	0.494	(0.823, 2.764)	1.810	0.562	(0.829, 3.024)
$γ F$	2.125	0.246	(1.655, 2.624)	2.238	0.254	(1.770, 2.758)
$γ G$	2.567	0.390	(1.866, 3.379)	2.764	0.431	(1.978, 3.695)
$γ H$	2.663	0.282	(2.151, 3.254)	2.699	0.287	(2.190, 3.310)
$γ I$	2.188	0.418	(1.419, 3.045)	2.383	0.466	(1.559, 3.387)

图A9 模拟研究中1P-ASM和2P-ASM在不同信息水平下的能力估计值对比

表A8 实证研究中SRM参数估计结果

状态转移倾向参数	均值	标准差	95%HPD	状态转移倾向参数	均值	标准差	95%HPD
$λ S A$	0.587	0.035	(0.519, 0.656)	$λ D S$	−0.886	0.107	(−1.101, −0.677)
$λ S F$	−0.587	0.035	(−0.656, −0.519)	$λ E D$	0.790	0.136	(0.523, 1.067)
$λ A B$	1.740	0.068	(1.608, 1.873)	$λ E J$	0.052	0.127	(−0.201, 0.308)
$λ A G$	−0.003	0.065	(−0.129, 0.125)	$λ E S$	−0.843	0.157	(−1.153, −0.542)
$λ A S$	−1.737	0.097	(−1.935, −1.554)	$λ F S$	−0.680	0.064	(−0.805, −0.557)
$λ B C$	1.586	0.075	(1.443, 1.738)	$λ F G$	0.680	0.064	(0.557, 0.805)
$λ B H$	0.165	0.076	(0.011, 0.320)	$λ G S$	−0.761	0.064	(−0.886, −0.635)
$λ B S$	−1.751	0.120	(−1.998, −1.523)	$λ G H$	0.761	0.064	(0.635, 0.886)
$λ C D$	1.785	0.082	(1.625, 1.946)	$λ H S$	0.373	0.064	(0.247, 0.503)
$λ C E$	−0.049	0.094	(−0.231, 0.132)	$λ H I$	−0.666	0.054	(−0.773, −0.560)
$λ C S$	−1.372	0.153	(−1.688, −1.086)	$λ H J$	0.293	0.045	(0.207, 0.381)
$λ C J$	−0.364	0.105	(−0.576, −0.163)	$λ I S$	0.171	0.089	(−0.007, 0.345)
$λ D J$	1.589	0.079	(1.433, 1.744)	$λ I J$	−0.171	0.089	(−0.345, 0.007)
$λ D E$	−0.702	0.099	(−0.897, −0.513)

表A8 实证研究中SRM参数估计结果

状态转移倾向参数	均值	标准差	95%HPD	状态转移倾向参数	均值	标准差	95%HPD
$λ S A$	0.587	0.035	(0.519, 0.656)	$λ D S$	−0.886	0.107	(−1.101, −0.677)
$λ S F$	−0.587	0.035	(−0.656, −0.519)	$λ E D$	0.790	0.136	(0.523, 1.067)
$λ A B$	1.740	0.068	(1.608, 1.873)	$λ E J$	0.052	0.127	(−0.201, 0.308)
$λ A G$	−0.003	0.065	(−0.129, 0.125)	$λ E S$	−0.843	0.157	(−1.153, −0.542)
$λ A S$	−1.737	0.097	(−1.935, −1.554)	$λ F S$	−0.680	0.064	(−0.805, −0.557)
$λ B C$	1.586	0.075	(1.443, 1.738)	$λ F G$	0.680	0.064	(0.557, 0.805)
$λ B H$	0.165	0.076	(0.011, 0.320)	$λ G S$	−0.761	0.064	(−0.886, −0.635)
$λ B S$	−1.751	0.120	(−1.998, −1.523)	$λ G H$	0.761	0.064	(0.635, 0.886)
$λ C D$	1.785	0.082	(1.625, 1.946)	$λ H S$	0.373	0.064	(0.247, 0.503)
$λ C E$	−0.049	0.094	(−0.231, 0.132)	$λ H I$	−0.666	0.054	(−0.773, −0.560)
$λ C S$	−1.372	0.153	(−1.688, −1.086)	$λ H J$	0.293	0.045	(0.207, 0.381)
$λ C J$	−0.364	0.105	(−0.576, −0.163)	$λ I S$	0.171	0.089	(−0.007, 0.345)
$λ D J$	1.589	0.079	(1.433, 1.744)	$λ I J$	−0.171	0.089	(−0.345, 0.007)
$λ D E$	−0.702	0.099	(−0.897, −0.513)

参考文献 48

[1]	Arieli-Attali, M., Ou, L., & Simmering, V. R. (2019). Understanding test takers' choices in a self-adapted test: A hidden Markov modeling of process data. Frontiers in Psychology, 10, 83. doi: 10.3389/fpsyg.2019.00083 pmid: 30787889
[2]	Beck, L. W. (1943). The principle of parsimony in empirical science. The Journal of Philosophy, 40(23), 617-633. https://doi.org/10.2307/2019692 doi: 10.2307/2019692 URL
[3]	Bergner, Y., Walker, E., & Ogan, A. (2017). Dynamic Bayesian network models for peer tutoring interactions. In A. A. vonDavier, M.Zhu, & P. C.Kyllonen(Eds), Innovative assessment of collaboration (pp. 249-268). Cham: Springer.
[4]	Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinee's ability. In F. M.Lord & M. R.Novick (Eds.), Statistical theories of mental test scores (pp. 397-124). Reading, MA: Addison-Wesley.
[5]	Bock, R. D. (1972). Estimating item parameters and latent ability when responses are scored in two or more nominal categories. Psychometrika, 37(1), 29-51. https://doi.org/10.1007/BF02291411 doi: 10.1007/BF02291411 URL
[6]	Buchner, A., & Funke, J. (1993). Finite-state automata: Dynamic task environments in problem-solving research. The Quarterly Journal of Experimental Psychology, 46(1), 83-118. doi: 10.1080/14640749308401068 URL
[7]	Chen, Y. (2020). A continuous-time dynamic choice measurement model for problem-solving process data. Psychometrika, 85(4), 1052-1075. doi: 10.1007/s11336-020-09734-1 pmid: 33346883
[8]	Fu, Y., Zhan, P., Chen, Q., & Jiao, H. (2022). Joint modeling of action sequences and action times in problem-solving tasks. PsyArXiv. Retrieved from psyarxiv.com/e3nbc
[9]	Vehtari, A., Gelman, A., & Gabry, J. (2017). Practical Bayesian model evaluation using leave-one-out cross- validation and WAIC. Statistics and Computing, 27, 1413-1432. doi: 10.1007/s11222-016-9696-4
[10]	Gelman, A., Meng, X.-L., & Stern, H. (1996). Posterior predictive assessment of model fitness via realized discrepancies. Statistica Sinica, 6, 733-760.
[11]	Gelman, A., & Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences. Statistical Science, 7, 457-511.
[12]	Han, Y., Liu, H., & Ji, F. (2022). A sequential response model for analyzing process data on technology-based problem- solving tasks. Multivariate Behavioral Research, 57(6), 960-977. doi: 10.1080/00273171.2021.1932403 URL
[13]	Han, Y., & Wilson, M. (2022). Analyzing student response processes to evaluate success on a technology-based problem-solving task. Applied Measurement in Education, 35(1), 33-45. doi: 10.1080/08957347.2022.2034821 URL
[14]	Han, Y., Xiao, Y., & Liu, H. (2022). Feature extraction and ability estimation of process data in the problem-solving test. Advances in Psychological Science, 30(6), 1393-1409. doi: 10.3724/SP.J.1042.2022.01393
	[ 韩雨婷, 肖悦, 刘红云. (2022). 问题解决测验中过程数据的特征抽取与能力评估. 心理科学进展, 30(6), 1393-1409.] doi: 10.3724/SP.J.1042.2022.01393
[15]	Hao, J., Shu, Z., & von Davier, A. (2015). Analyzing process data from game/scenario-based tasks: An edit distance approach. Journal of Educational Data Mining, 7(1), 33-50.
[16]	Harding, S. M. E., Griffin, P. E., Awwal, N., Alom, B. M., & Scoular, C. (2017). Measuring collaborative problem solving using mathematics-based tasks. AERA Open, 3(3), 1-19.
[17]	He, Q., Borgonovi, F., & Paccagnella, M. (2021). Leveraging process data to assess adults’ problem-solving skills: Using sequence mining to identify behavioral patterns across digital tasks. Computers & Education, 166, 104170. doi: 10.1016/j.compedu.2021.104170 URL
[18]	He, Q., & von Davier, M. (2016). Analyzing process data from problem-solving items with N-grams:Insights from a computer-based large-scale assessment. In R.Yigal, F.Steve, & M.Maryam (Eds.), Handbook of research on technology tools for real-world skill development (pp. 749-776). Hershey, PA: Information Science Reference.
[19]	Hoffman, M. D., & Gelman, A. (2014). The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. Journal of Machine Learning Research, 15(1), 1593-1623.
[20]	LaMar, M. M. (2018). Markov decision process measurement model. Psychometrika, 83(1), 67-88. doi: 10.1007/s11336-017-9570-0 pmid: 28447309
[21]	Levy, R. (2019). Dynamic Bayesian network modeling of game-based diagnostic assessments. Multivariate Behavioral Research, 54(6), 771-794. doi: 10.1080/00273171.2019.1590794 pmid: 30942094
[22]	Li, M., Liu, Y., Liu, H. (2020). Analysis of the Problem- solving strategies in computer-based dynamic assessment: The extension and application of multilevel mixture IRT model. Acta Psychologica Sinica, 52(4), 528-540. doi: 10.3724/SP.J.1041.2020.00528 URL
	[ 李美娟, 刘玥, 刘红云. (2020). 计算机动态测验中问题解决过程策略的分析: 多水平混合IRT模型的拓展与应用. 心理学报, 52(4), 528-540.] doi: 10.3724/SP.J.1041.2020.00528
[23]	Liu, H., Liu, Y., & Li, M. (2018). Analysis of process data of PISA 2012 computer-based problem solving: Application of the modified multilevel mixture IRT model. Frontiers in Psychology, 9, 1372. doi: 10.3389/fpsyg.2018.01372 pmid: 30123171
[24]	Liu, Y., Xu, H., Chen, Q., & Zhan, P. (2022). The measurement of problem-solving competence using process data. Advances in Psychological Science, 30(3), 522-535. doi: 10.3724/SP.J.1042.2022.00522
	[ 刘耀辉, 徐慧颖, 陈琦鹏, 詹沛达. (2022). 基于过程数据的问题解决能力测量及数据分析方法. 心理科学进展, 30(3), 522-535.] doi: 10.3724/SP.J.1042.2022.00522
[25]	Ma, W., Iaconangelo, C., & de la Torre, J. (2016). Model similarity, model selection, and attribute classification. Applied Psychological Measurement, 40(3), 200-217. doi: 10.1177/0146621615621717 pmid: 29881048
[26]	Man, K., Harring, J. R., & Zhan, P. (2022). Bridging models of biometric and psychometric assessment: A three-way joint modeling approach of item responses, response times and gaze fixation counts. Applied Psychological Measurement, 46(5), 361-381. doi: 10.1177/01466216221089344 URL
[27]	Newell, A., & Simon, H. A. (1972). Human problem solving (Vol. 104, No. 9). Englewood Cliffs, NJ: Prentice-hall.
[28]	OECD. (2013). PISA 2012 assessment and analytical framework: Mathematics, reading, science, problem solving and financial literacy. OECD Publishing. http://dx.doi.org/10.1787/9789264190511-en
[29]	Peng, S., Cai, Y., Wang, D., Luo, F., & Tu, D. (2022). A generalized diagnostic classification modeling framework integrating differential speediness: Advantages and illustrations in psychological and educational testing. Multivariate Behavioral Research, 57(6), 940-959. doi: 10.1080/00273171.2021.1928474 URL
[30]	Rasch, G. (1960). On general laws and the meaning of measurement in psychology. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability:Held at the Statistical Laboratory, University of California, June 20-July 30, 1960 (Vol. 4, p. 321). University of California Press.
[31]	Rosen, Y. (2017). Assessing students in human-to-agent settings to inform collaborative problem-solving learning. Journal of Educational Measurement, 54(1), 36-53. doi: 10.1111/jedm.2017.54.issue-1 URL
[32]	Shu, Z., Bergner, Y., Zhu, M., Hao, J., & von Davier, A. A. (2017). An item response theory analysis of problem- solving processes in scenario-based tasks. Psychological Test and Assessment Modeling, 59(1), 109-131.
[33]	Tang, X., Wang, Z., He, Q., Liu, J., & Ying, Z. (2020). Latent feature extraction for process data via multidimensional scaling. Psychometrika, 85(2), 378-397. doi: 10.1007/s11336-020-09708-3 pmid: 32572672
[34]	Tang, X., Wang, Z., Liu, J., & Ying, Z. (2021). An exploratory analysis of the latent structure of process data via action sequence autoencoders. British Journal of Mathematical and Statistical Psychology, 74(1), 1-33.
[35]	van der Linden, W. J. (2006). A lognormal model for response times on test items. Journal of Educational and Behavioral Statistics, 31(2), 181-204.
[36]	van der Linden, W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items. Psychometrika, 72(3), 287-308. doi: 10.1007/s11336-006-1478-z URL
[37]	Vista, A., Care, E., & Awwal, N. (2017). Visualising and examining sequential actions as behavioural paths that can be interpreted as markers of complex behaviours. Computers in Human Behavior, 76, 656-671. doi: 10.1016/j.chb.2017.01.027 URL
[38]	Watanabe, S. (2010). Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. Journal of Machine Learning Research, 11(12), 3571-3594..
[39]	Wilson, M., Gochyyev, P., & Scalise, K. (2017). Modeling data from collaborative assessments: learning in digital interactive social networks. Journal of Educational Measurement, 54(1), 85-102. doi: 10.1111/jedm.2017.54.issue-1 URL
[40]	Xiao, Y., He, Q., Veldkamp, B., & Liu, H. (2021). Exploring latent states of problem-solving competence using hidden Markov model on process data. Journal of Computer Assisted Learning, 37(5), 1232-1247. doi: 10.1111/jcal.v37.5 URL
[41]	Xiao, Y., & Liu, H. (2023). A state response measurement model for problem-solving process data. Behavior Research Methods, Online First.
[42]	Yuan, J., Xiao, Y., & Liu, H. (2019). Assessment of collaborative problem solving based on process stream data: A new paradigm for extracting indicators and modeling dyad data. Frontiers in Psychology, 10, 369. doi: 10.3389/fpsyg.2019.00369 pmid: 30863344
[43]	Zhan, P., Jiao, H., & Liao, D. (2018). Cognitive diagnosis modelling incorporating item response times. British Journal of Mathematical and Statistical Psychology, 71(2), 262-286. doi: 10.1111/bmsp.2018.71.issue-2 URL
[44]	Zhan, P., Man, K., Wind, S. A., & Malone, J. (2022). Cognitive diagnosis modeling incorporating response times and fixation counts: Providing comprehensive feedback and accurate diagnosis. Journal of Educational and Behavioral Statistics, 47(6), 736-776.
[45]	Zhan, P., & Qiao, X. (2022). Diagnostic classification analysis of problem-solving competence using process data: An item expansion method. Psychometrika, 87(4), 1529-1547. doi: 10.1007/s11336-022-09855-9 pmid: 35389193
[46]	Zhan, S., Hao, J., & Davier, A. V. (2015). Analyzing process data from game/scenariobased tasks: An edit distance approach. Journal of Educational Data Mining, 7(1), 33-50.
[47]	Zhang, S., Wang, Z., Qi, J., Liu, J., & Ying, Z. (2022). Accurate assessment via process data. Psychometrika, 88(1), 76-97. doi: 10.1007/s11336-022-09880-8 pmid: 35962849
[48]	Zhu, M., Shu, Z., & von Davier, A. A. (2016). Using networks to visualize and analyze process data for educational assessment. Journal of Educational Measurement, 53(2), 190-211. doi: 10.1111/jedm.12107 URL