

CN 11-1911/B


Acta Psychologica Sinica ›› 2023, Vol. 55 ›› Issue (8): 1383-1396.doi: 10.3724/SP.J.1041.2023.01383
• Reports of Empirical Studies • Previous Articles
FU Yanbin, CHEN Qipeng, ZHAN Peida( )
)
Received:2023-01-04
Published:2023-08-25
Online:2023-05-12
Contact:
Peida Zhan, E-mail: pdzhan@gmail.com
Supported by:FU Yanbin, CHEN Qipeng, ZHAN Peida. (2023). Binary modeling of action sequences in problem-solving tasks: One- and two-parameter action sequence model. Acta Psychologica Sinica, 55(8), 1383-1396.
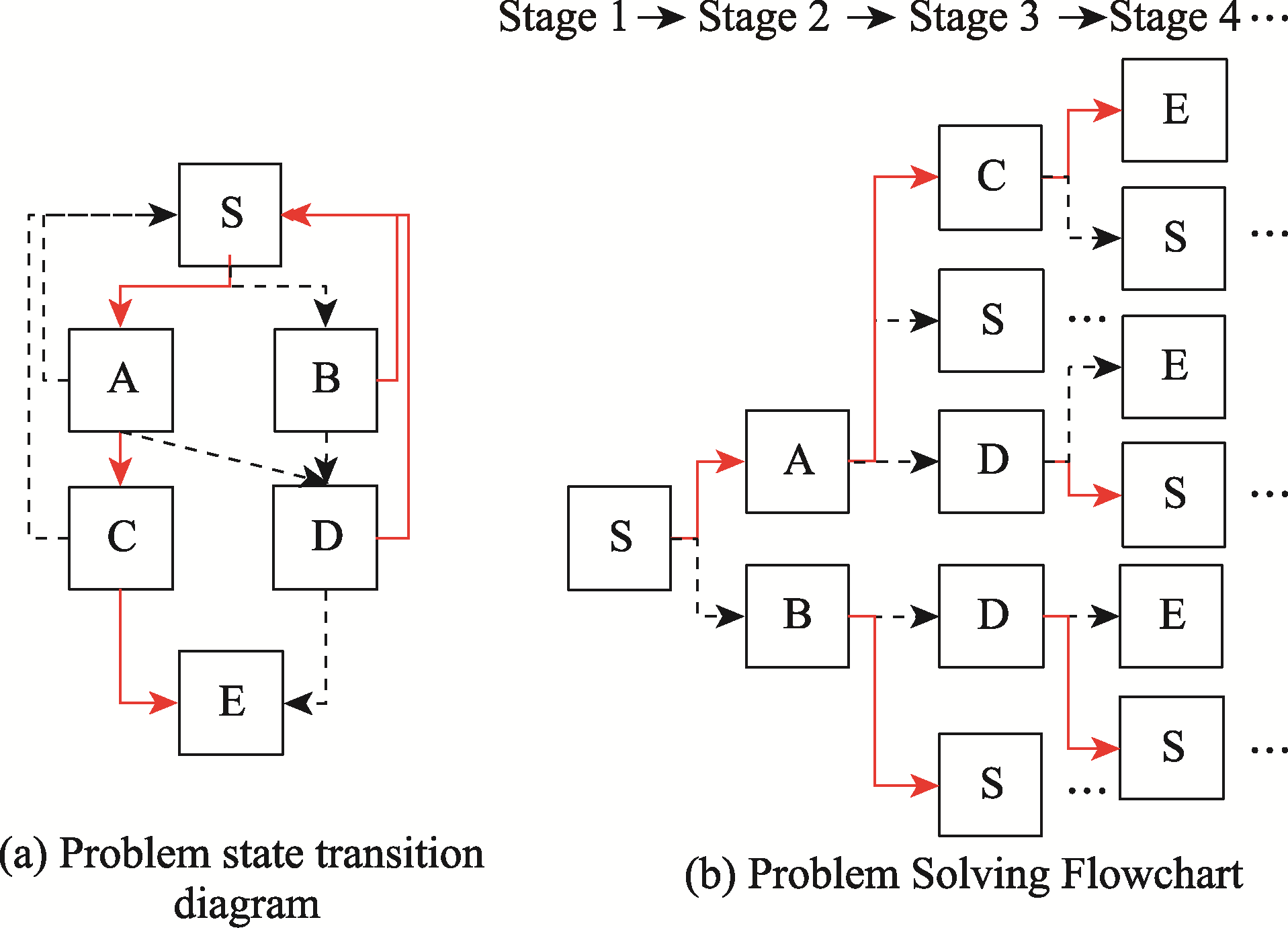
Figure 1. Schematic Diagram of Problem-Solving Task. Note. The red solid arrows represent correct state transitions, while the black dashed arrows indicate incorrect state transitions. The optimal action sequence is S→A→C→E, which includes the three state transitions S→A, A→C, and C→E. Ellipses signify the recurring appearance of the problem-solving process.

Figure 2. Schematic Diagram of the Sequential Response Model. Note. θn represents the problem-solving ability of participant n; Sn1 represents the problem state of participant n at stage 1, and so on; Sn1→Sn2 represents the state transition of participant n moving from stage 1 to stage 2, and so forth.
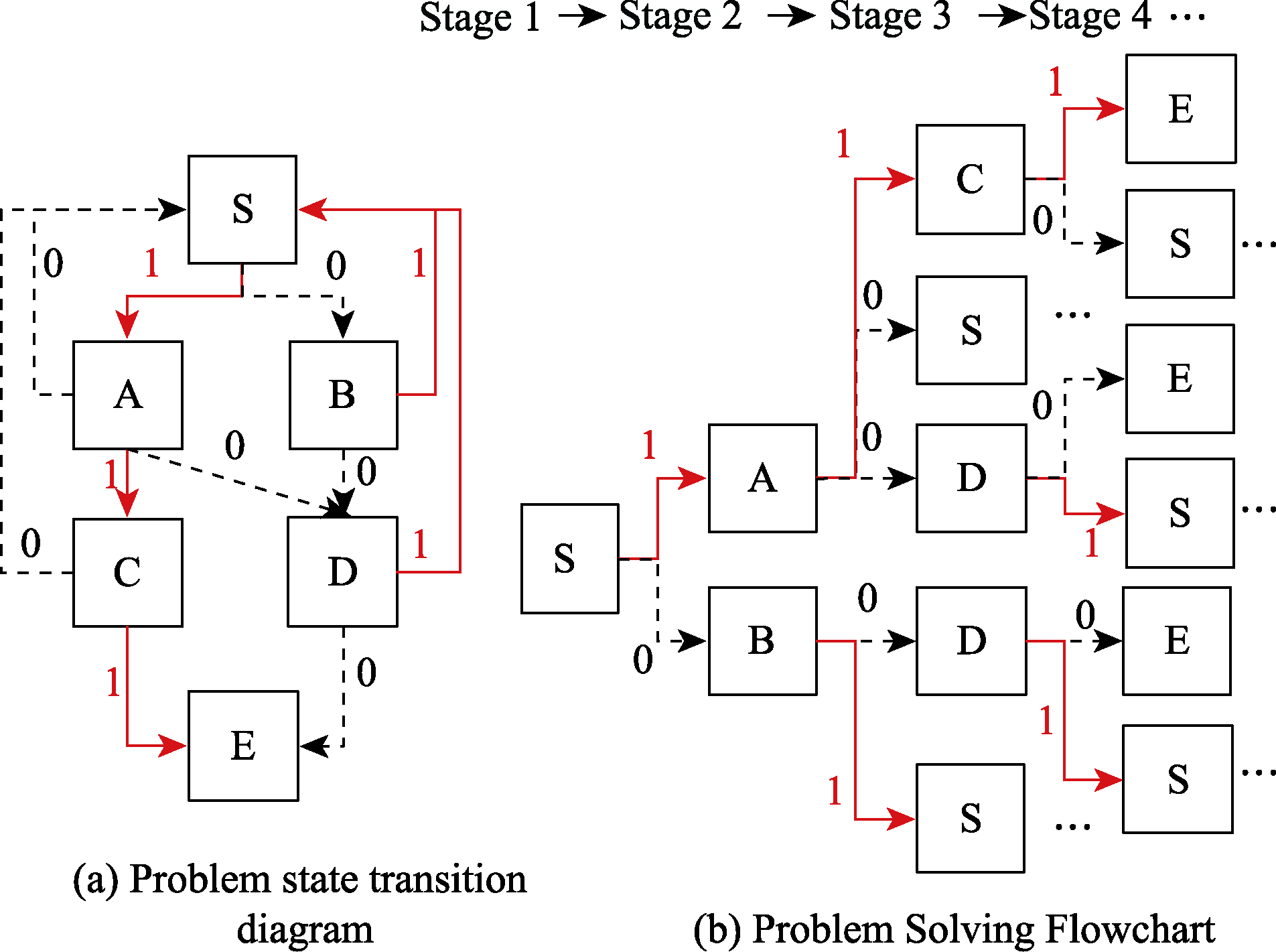
Figure 3. Binary Encoding for Problem-Solving Task. Note. The red solid arrows represent correct state transitions, coded as 1; the black dashed arrows represent incorrect state transitions, coded as 0; the ellipsis represents the repeated occurrence of the problem-solving process.
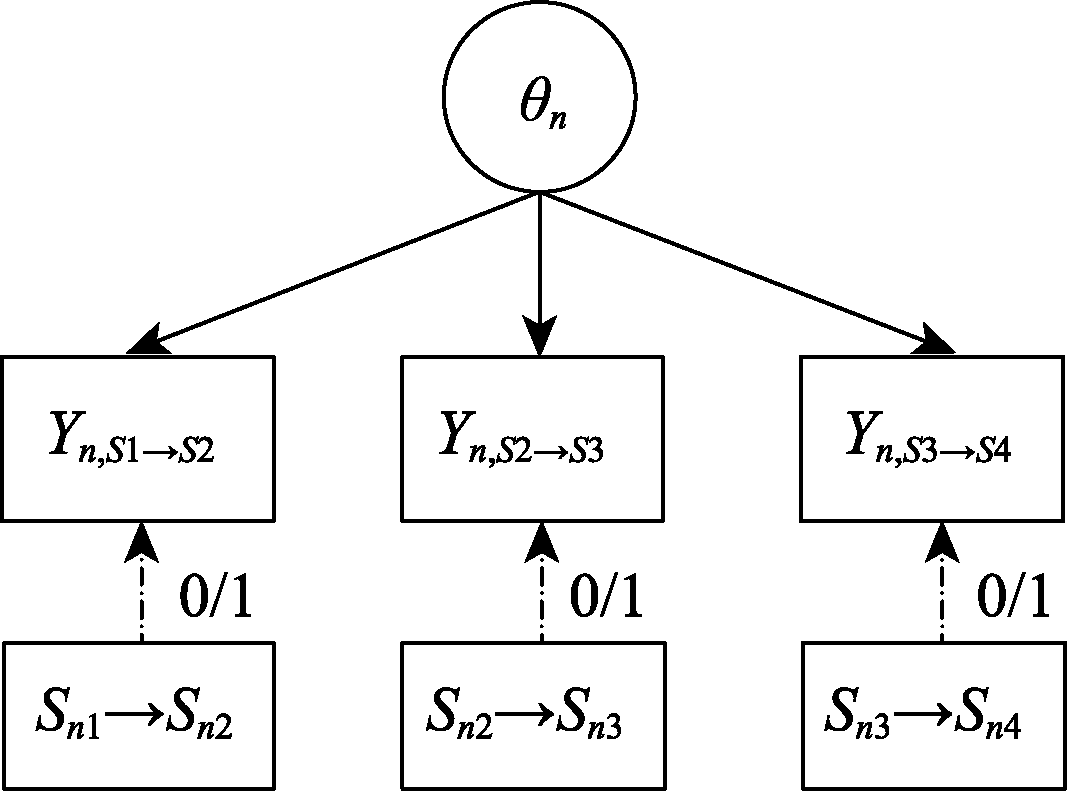
Figure 4. Schematic Diagram of the Binary Modeling of Action Sequences. Note. θn is the problem-solving ability of participant n; Sn1 is the problem state of participant n in stage 1, and so on; Sn1→Sn2 is the state transition of participant n from stage 1 to stage 2, and so on; Yn,S1→S2 is the state transition after binary coding, Yn,S1→S2 = 1 means that participant n has presented the correct state transition, Yn,S1→S2 = 0 means that participant n has presented the wrong state transition; Action sequences vary in length and number of boxes.
| States in Current Stage (Items) | States in the Next Stage (Options) | |||
|---|---|---|---|---|
| S | A (1) | F (0) | ||
| A | B (1) | G (0) | S (0) | |
| B | C (1) | H (0) | S (0) | |
| C | D (1) | E (0) | S (0) | J (0) |
| D | J (1) | E (0) | S (0) | |
| E | D (1) | J (0) | S (0) | |
| F | S (1) | G (0) | ||
| G | S (1) | H (0) | ||
| H | S (1) | I (0) | J (0) | |
| I | S (1) | J (0) | ||
Table 1 Understanding the TICKETS Task (CP038Q02) from the “Multiple-Choice Item” Perspective.
| States in Current Stage (Items) | States in the Next Stage (Options) | |||
|---|---|---|---|---|
| S | A (1) | F (0) | ||
| A | B (1) | G (0) | S (0) | |
| B | C (1) | H (0) | S (0) | |
| C | D (1) | E (0) | S (0) | J (0) |
| D | J (1) | E (0) | S (0) | |
| E | D (1) | J (0) | S (0) | |
| F | S (1) | G (0) | ||
| G | S (1) | H (0) | ||
| H | S (1) | I (0) | J (0) | |
| I | S (1) | J (0) | ||
| Model | LOO | WAIC | ppp | Computational time (in seconds) |
|---|---|---|---|---|
| 1P-ASM | 11018.208 | 11007.133 | 0.511 | 647.5 |
| 2P-ASM | 10363.785 | 10275.475 | 0.518 | 958.5 |
| SRM | 16804.501 | 16803.925 | 0.498 | 1958.6 |
Table 2 The Fitting Performance and The Computational Time in The Empirical Study.
| Model | LOO | WAIC | ppp | Computational time (in seconds) |
|---|---|---|---|---|
| 1P-ASM | 11018.208 | 11007.133 | 0.511 | 647.5 |
| 2P-ASM | 10363.785 | 10275.475 | 0.518 | 958.5 |
| SRM | 16804.501 | 16803.925 | 0.498 | 1958.6 |
| Current State | 1P-ASM | 2P-ASM | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Action easiness parameter | Action easiness parameter | Action discrimination parameter | |||||||
| Posterior Mean | Posterior Standard Deviation | 95% HPD | Posterior Mean | Posterior Standard Deviation | 95% HPD | Posterior Mean | Posterior Standard Deviation | 95% HPD | |
| S | 0.911 | 0.046 | (0.822, 1.001) | 0.969 | 0.057 | (0.860, 1.084) | 1.343 | 0.116 | (1.111, 1.570) |
| A | 1.553 | 0.066 | (1.425, 1.682) | 1.547 | 0.077 | (1.401, 1.701) | 1.457 | 0.212 | (1.043, 1.870) |
| B | 1.432 | 0.073 | (1.290, 1.577) | 1.354 | 0.082 | (1.198, 1.521) | 1.797 | 0.398 | (0.958, 2.566) |
| C | 1.436 | 0.080 | (1.279, 1.599) | 1.207 | 0.148 | (0.940, 1.526) | 3.015 | 0.885 | (1.104, 4.759) |
| E | 2.008 | 0.107 | (1.801, 2.215) | 1.734 | 0.159 | (1.456, 2.099) | 1.615 | 0.495 | (0.463, 2.576) |
| D | 0.361 | 0.176 | (0.015, 0.702) | 0.472 | 0.283 | (?0.031, 1.064) | 1.472 | 0.952 | (0.225, 3.792) |
| F | ?1.705 | 0.107 | (?1.918, ?1.492) | ?1.590 | 0.123 | (?1.829, ?1.348) | 1.438 | 0.250 | (0.982, 1.974) |
| G | ?1.888 | 0.111 | (?2.105, ?1.677) | ?1.747 | 0.147 | (?2.050, ?1.480) | 2.115 | 0.354 | (1.495, 2.875) |
| H | ?0.749 | 0.075 | (?0.898, ?0.599) | ?0.292 | 0.172 | (?0.636, 0.037) | 2.229 | 0.426 | (1.400, 3.088) |
| I | ?0.368 | 0.157 | (?0.686, 0.062) | 0.760 | 0.470 | (?0.101, 1.753) | 3.127 | 0.933 | (1.525, 5.179) |
Table 3 The Parameter Estimation Results of ASM in Empirical Study.
| Current State | 1P-ASM | 2P-ASM | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Action easiness parameter | Action easiness parameter | Action discrimination parameter | |||||||
| Posterior Mean | Posterior Standard Deviation | 95% HPD | Posterior Mean | Posterior Standard Deviation | 95% HPD | Posterior Mean | Posterior Standard Deviation | 95% HPD | |
| S | 0.911 | 0.046 | (0.822, 1.001) | 0.969 | 0.057 | (0.860, 1.084) | 1.343 | 0.116 | (1.111, 1.570) |
| A | 1.553 | 0.066 | (1.425, 1.682) | 1.547 | 0.077 | (1.401, 1.701) | 1.457 | 0.212 | (1.043, 1.870) |
| B | 1.432 | 0.073 | (1.290, 1.577) | 1.354 | 0.082 | (1.198, 1.521) | 1.797 | 0.398 | (0.958, 2.566) |
| C | 1.436 | 0.080 | (1.279, 1.599) | 1.207 | 0.148 | (0.940, 1.526) | 3.015 | 0.885 | (1.104, 4.759) |
| E | 2.008 | 0.107 | (1.801, 2.215) | 1.734 | 0.159 | (1.456, 2.099) | 1.615 | 0.495 | (0.463, 2.576) |
| D | 0.361 | 0.176 | (0.015, 0.702) | 0.472 | 0.283 | (?0.031, 1.064) | 1.472 | 0.952 | (0.225, 3.792) |
| F | ?1.705 | 0.107 | (?1.918, ?1.492) | ?1.590 | 0.123 | (?1.829, ?1.348) | 1.438 | 0.250 | (0.982, 1.974) |
| G | ?1.888 | 0.111 | (?2.105, ?1.677) | ?1.747 | 0.147 | (?2.050, ?1.480) | 2.115 | 0.354 | (1.495, 2.875) |
| H | ?0.749 | 0.075 | (?0.898, ?0.599) | ?0.292 | 0.172 | (?0.636, 0.037) | 2.229 | 0.426 | (1.400, 3.088) |
| I | ?0.368 | 0.157 | (?0.686, 0.062) | 0.760 | 0.470 | (?0.101, 1.753) | 3.127 | 0.933 | (1.525, 5.179) |
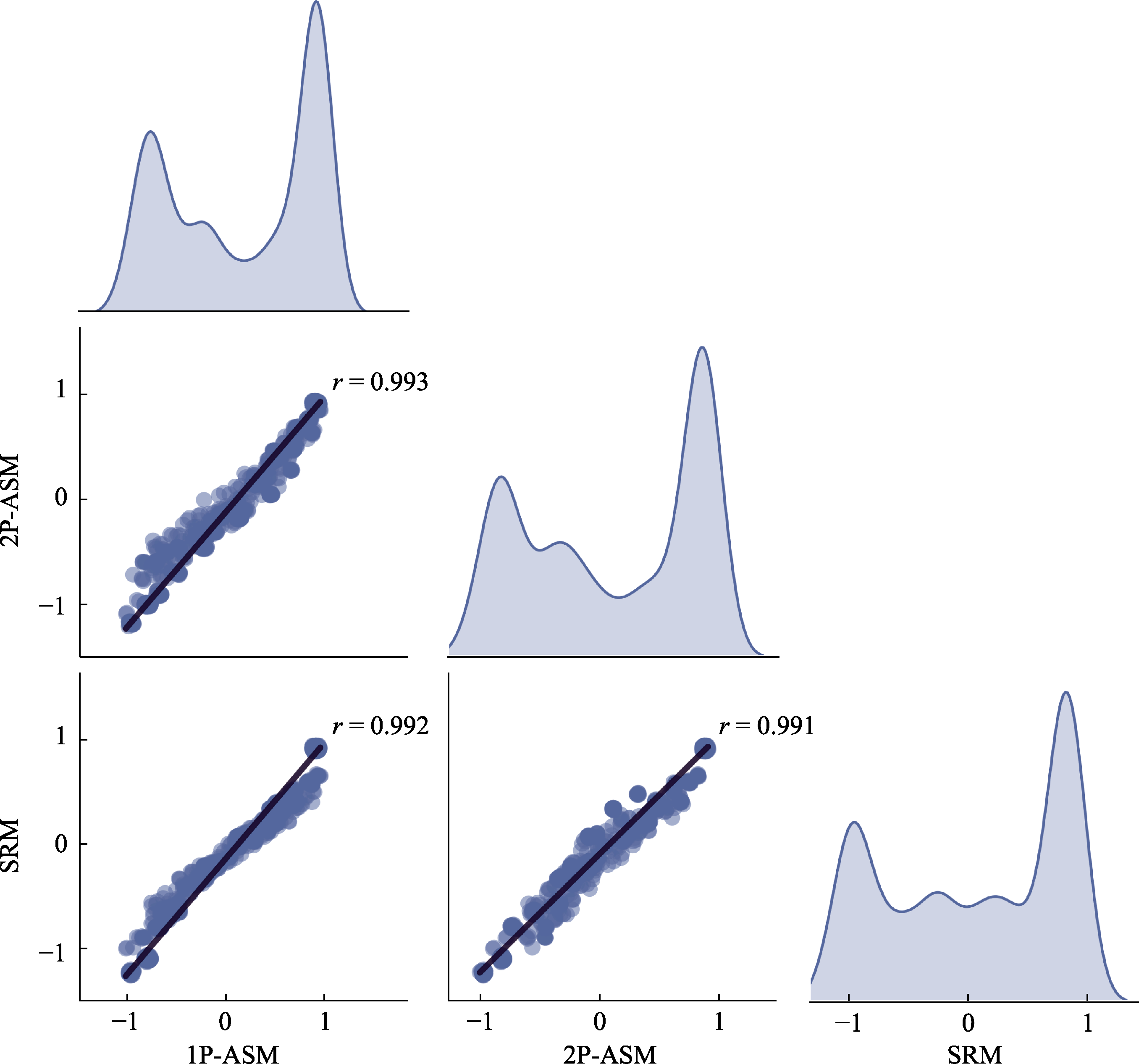
Figure 7. Scatter Plots and Probability Density Plots of the Problem-Solving Ability Estimates Across the Three Models. Note. 1P-ASM = one-parameter action sequence model; 2P-ASM = two-parameter action sequence model; SRM = sequential response model; r = Pearson correlation.
| State transition sequence | Frequency | SRM | 1P-ASM | 2P-ASM | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Median | Standard Deviation | Mean | Median | Standard Deviation | Mean | Median | Standard Deviation | ||
| SABCDJ | 737 | 0.837 | 0.837 | 0.011 | 0.821 | 0.821 | 0.009 | 0.666 | 0.665 | 0.012 |
| SFSABCDJ | 35 | 0.525 | 0.525 | 0.007 | 0.676 | 0.677 | 0.007 | 0.604 | 0.603 | 0.010 |
| SFGSABCDJ | 22 | 0.345 | 0.347 | 0.007 | 0.598 | 0.598 | 0.005 | 0.488 | 0.487 | 0.009 |
| SABCEDJ | 23 | 0.279 | 0.279 | 0.007 | ?0.017 | ?0.018 | 0.005 | 0.257 | 0.258 | 0.008 |
| SFGHSABCDJ | 52 | 0.152 | 0.151 | 0.006 | 0.304 | 0.304 | 0.004 | 0.295 | 0.296 | 0.009 |
| SABCJ | 47 | 0.023 | 0.025 | 0.007 | ?0.238 | ?0.237 | 0.006 | ?0.035 | ?0.035 | 0.011 |
| SABCEJ | 27 | ?0.250 | ?0.250 | 0.005 | ?0.404 | ?0.404 | 0.005 | ?0.338 | ?0.338 | 0.012 |
| SABHJ | 117 | ?0.364 | ?0.364 | 0.007 | ?0.506 | ?0.506 | 0.006 | ?0.359 | ?0.358 | 0.010 |
| SAGHJ | 65 | ?0.662 | ?0.662 | 0.008 | ?0.741 | ?0.742 | 0.008 | ?0.594 | ?0.594 | 0.010 |
| SAGHIJ | 45 | ?0.806 | ?0.806 | 0.008 | ?0.940 | ?0.939 | 0.007 | ?0.760 | ?0.760 | 0.010 |
| SFGHJ | 337 | ?1.099 | ?1.099 | 0.011 | ?1.033 | ?1.033 | 0.008 | ?0.869 | ?0.869 | 0.011 |
| SFGHIJ | 95 | ?1.228 | ?1.227 | 0.011 | ?1.201 | ?1.201 | 0.008 | ?1.020 | ?1.021 | 0.010 |
Table 4 Descriptive Statistics of Latent Ability for Selected Action sequence
| State transition sequence | Frequency | SRM | 1P-ASM | 2P-ASM | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Median | Standard Deviation | Mean | Median | Standard Deviation | Mean | Median | Standard Deviation | ||
| SABCDJ | 737 | 0.837 | 0.837 | 0.011 | 0.821 | 0.821 | 0.009 | 0.666 | 0.665 | 0.012 |
| SFSABCDJ | 35 | 0.525 | 0.525 | 0.007 | 0.676 | 0.677 | 0.007 | 0.604 | 0.603 | 0.010 |
| SFGSABCDJ | 22 | 0.345 | 0.347 | 0.007 | 0.598 | 0.598 | 0.005 | 0.488 | 0.487 | 0.009 |
| SABCEDJ | 23 | 0.279 | 0.279 | 0.007 | ?0.017 | ?0.018 | 0.005 | 0.257 | 0.258 | 0.008 |
| SFGHSABCDJ | 52 | 0.152 | 0.151 | 0.006 | 0.304 | 0.304 | 0.004 | 0.295 | 0.296 | 0.009 |
| SABCJ | 47 | 0.023 | 0.025 | 0.007 | ?0.238 | ?0.237 | 0.006 | ?0.035 | ?0.035 | 0.011 |
| SABCEJ | 27 | ?0.250 | ?0.250 | 0.005 | ?0.404 | ?0.404 | 0.005 | ?0.338 | ?0.338 | 0.012 |
| SABHJ | 117 | ?0.364 | ?0.364 | 0.007 | ?0.506 | ?0.506 | 0.006 | ?0.359 | ?0.358 | 0.010 |
| SAGHJ | 65 | ?0.662 | ?0.662 | 0.008 | ?0.741 | ?0.742 | 0.008 | ?0.594 | ?0.594 | 0.010 |
| SAGHIJ | 45 | ?0.806 | ?0.806 | 0.008 | ?0.940 | ?0.939 | 0.007 | ?0.760 | ?0.760 | 0.010 |
| SFGHJ | 337 | ?1.099 | ?1.099 | 0.011 | ?1.033 | ?1.033 | 0.008 | ?0.869 | ?0.869 | 0.011 |
| SFGHIJ | 95 | ?1.228 | ?1.227 | 0.011 | ?1.201 | ?1.201 | 0.008 | ?1.020 | ?1.021 | 0.010 |
| Sample size | Action sequence length | Model | Bias | RMSE | Cor | ART (in seconds) |
|---|---|---|---|---|---|---|
| 100 | Short | 1P-ASM | ?0.002 | 0.534 | 0.854 | 18.117 |
| 2P-ASM | ?0.002 | 0.534 | 0.852 | 30.274 | ||
| SRM | 0.007 | 0.515 | 0.863 | 1029.189 | ||
| Long | 1P-ASM | ?0.011 | 0.441 | 0.910 | 24.393 | |
| 2P-ASM | ?0.011 | 0.408 | 0.917 | 37.100 | ||
| SRM | ?0.026 | 0.395 | 0.921 | 1321.361 | ||
| 200 | Short | 1P-ASM | 0.007 | 0.523 | 0.855 | 41.923 |
| 2P-ASM | 0.007 | 0.518 | 0.858 | 66.395 | ||
| SRM | 0.011 | 0.507 | 0.864 | 527.740 | ||
| Long | 1P-ASM | 0.010 | 0.438 | 0.912 | 54.448 | |
| 2P-ASM | 0.010 | 0.395 | 0.921 | 76.707 | ||
| SRM | 0.002 | 0.386 | 0.924 | 691.308 | ||
| 500 | Short | 1P-ASM | ?0.004 | 0.516 | 0.856 | 119.439 |
| 2P-ASM | ?0.004 | 0.504 | 0.863 | 198.838 | ||
| SRM | ?0.001 | 0.500 | 0.865 | 590.051 | ||
| Long | 1P-ASM | 0.005 | 0.444 | 0.907 | 160.661 | |
| 2P-ASM | 0.005 | 0.394 | 0.920 | 236.195 | ||
| SRM | 0.002 | 0.391 | 0.921 | 801.767 |
Table 5 Parameter Estimation Accuracy of Latent Ability and Computational Time in the Simulation Study
| Sample size | Action sequence length | Model | Bias | RMSE | Cor | ART (in seconds) |
|---|---|---|---|---|---|---|
| 100 | Short | 1P-ASM | ?0.002 | 0.534 | 0.854 | 18.117 |
| 2P-ASM | ?0.002 | 0.534 | 0.852 | 30.274 | ||
| SRM | 0.007 | 0.515 | 0.863 | 1029.189 | ||
| Long | 1P-ASM | ?0.011 | 0.441 | 0.910 | 24.393 | |
| 2P-ASM | ?0.011 | 0.408 | 0.917 | 37.100 | ||
| SRM | ?0.026 | 0.395 | 0.921 | 1321.361 | ||
| 200 | Short | 1P-ASM | 0.007 | 0.523 | 0.855 | 41.923 |
| 2P-ASM | 0.007 | 0.518 | 0.858 | 66.395 | ||
| SRM | 0.011 | 0.507 | 0.864 | 527.740 | ||
| Long | 1P-ASM | 0.010 | 0.438 | 0.912 | 54.448 | |
| 2P-ASM | 0.010 | 0.395 | 0.921 | 76.707 | ||
| SRM | 0.002 | 0.386 | 0.924 | 691.308 | ||
| 500 | Short | 1P-ASM | ?0.004 | 0.516 | 0.856 | 119.439 |
| 2P-ASM | ?0.004 | 0.504 | 0.863 | 198.838 | ||
| SRM | ?0.001 | 0.500 | 0.865 | 590.051 | ||
| Long | 1P-ASM | 0.005 | 0.444 | 0.907 | 160.661 | |
| 2P-ASM | 0.005 | 0.394 | 0.920 | 236.195 | ||
| SRM | 0.002 | 0.391 | 0.921 | 801.767 |
| Sample size | Action sequence length | 1P-ASM and SRM | 2P-ASM and SRM | ||||
|---|---|---|---|---|---|---|---|
| CBias | CRMSE | Ccor | Cbias | CRMSE | Ccor | ||
| 100 | Short | ?0.009 | 0.126 | 0.991 | ?0.009 | 0.129 | 0.989 |
| Long | 0.015 | 0.200 | 0.986 | 0.015 | 0.098 | 0.995 | |
| 200 | Short | ?0.004 | 0.126 | 0.991 | ?0.004 | 0.098 | 0.994 |
| Long | 0.008 | 0.208 | 0.986 | 0.008 | 0.077 | 0.997 | |
| 500 | Short | ?0.002 | 0.126 | 0.990 | ?0.002 | 0.060 | 0.998 |
| Long | 0.003 | 0.211 | 0.986 | 0.003 | 0.042 | 0.999 | |
Table 6 Consistency of Latent Ability Estimates Among the Two ASMs and SRM in the Simulation Study
| Sample size | Action sequence length | 1P-ASM and SRM | 2P-ASM and SRM | ||||
|---|---|---|---|---|---|---|---|
| CBias | CRMSE | Ccor | Cbias | CRMSE | Ccor | ||
| 100 | Short | ?0.009 | 0.126 | 0.991 | ?0.009 | 0.129 | 0.989 |
| Long | 0.015 | 0.200 | 0.986 | 0.015 | 0.098 | 0.995 | |
| 200 | Short | ?0.004 | 0.126 | 0.991 | ?0.004 | 0.098 | 0.994 |
| Long | 0.008 | 0.208 | 0.986 | 0.008 | 0.077 | 0.997 | |
| 500 | Short | ?0.002 | 0.126 | 0.990 | ?0.002 | 0.060 | 0.998 |
| Long | 0.003 | 0.211 | 0.986 | 0.003 | 0.042 | 0.999 | |
| Model | Correct transition | Incorrect transition | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | … | K | |
| Sequential response model | P1 | P2 | P3 | … | PK |
| State response model | P1 | (I-P1)/(K-I) | (I-P1)/(K-I) | (I-P1)/(K-I) | |
| Action sequence model | P1 | I-P1 | |||
Table A1 Comparison of Three Action Sequence Data Analysis Models.
| Model | Correct transition | Incorrect transition | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | … | K | |
| Sequential response model | P1 | P2 | P3 | … | PK |
| State response model | P1 | (I-P1)/(K-I) | (I-P1)/(K-I) | (I-P1)/(K-I) | |
| Action sequence model | P1 | I-P1 | |||
| Cnt | SchoolID | StdID | Event | Time | Event Number | Action |
|---|---|---|---|---|---|---|
| ARE | 0000068 | 01770 | START_ITEM | 843.1000 | 1.00 | NULL |
| ARE | 0000068 | 01770 | ACER_EVENT | 885.2000 | 2.00 | country_trains |
| ARE | 0000068 | 01770 | ACER_EVENT | 892.3000 | 3.00 | full_fare |
| ARE | 0000068 | 01770 | ACER_EVENT | 894.1000 | 4.00 | daily |
| ARE | 0000068 | 01770 | ACER_EVENT | 904.5000 | 5.00 | Cancel |
| ARE | 0000068 | 01770 | ACER_EVENT | 914.7000 | 6.00 | country_trains |
| ARE | 0000068 | 01770 | ACER_EVENT | 915.0000 | 7.00 | full_fare |
| ARE | 0000068 | 01770 | ACER_EVENT | 915.9000 | 8.00 | individual |
| ARE | 0000068 | 01770 | ACER_EVENT | 917.5000 | 9.00 | trip_2 |
| ARE | 0000068 | 01770 | ACER_EVENT | 923.0000 | 10.00 | Buy |
| ARE | 0000068 | 01770 | END_ITEM | 928.5000 | 11.00 | NULL |
| ARE | 0000068 | 01770 | END_ITEM | 928.5000 | 12.00 | NULL |
| ARE | 0000068 | 01770 | ACER_EVENT | 923.0000 | 13.00 | Buy |
| ARE | 0000068 | 01770 | ACER_EVENT | 917.5000 | 14.00 | trip_2 |
| ARE | 0000068 | 01770 | ACER_EVENT | 915.9000 | 15.00 | individual |
| ARE | 0000068 | 01770 | ACER_EVENT | 915.0000 | 16.00 | full_fare |
| ARE | 0000068 | 01770 | ACER_EVENT | 914.7000 | 17.00 | country_trains |
| ARE | 0000068 | 01770 | ACER_EVENT | 904.5000 | 18.00 | Cancel |
| ARE | 0000068 | 01770 | ACER_EVENT | 894.1000 | 19.00 | daily |
| ARE | 0000068 | 01770 | ACER_EVENT | 892.3000 | 20.00 | full_fare |
| ARE | 0000068 | 01770 | ACER_EVENT | 885.2000 | 21.00 | country_trains |
Table A2 An Example of Anomalous Action Sequence in Empirical Study.
| Cnt | SchoolID | StdID | Event | Time | Event Number | Action |
|---|---|---|---|---|---|---|
| ARE | 0000068 | 01770 | START_ITEM | 843.1000 | 1.00 | NULL |
| ARE | 0000068 | 01770 | ACER_EVENT | 885.2000 | 2.00 | country_trains |
| ARE | 0000068 | 01770 | ACER_EVENT | 892.3000 | 3.00 | full_fare |
| ARE | 0000068 | 01770 | ACER_EVENT | 894.1000 | 4.00 | daily |
| ARE | 0000068 | 01770 | ACER_EVENT | 904.5000 | 5.00 | Cancel |
| ARE | 0000068 | 01770 | ACER_EVENT | 914.7000 | 6.00 | country_trains |
| ARE | 0000068 | 01770 | ACER_EVENT | 915.0000 | 7.00 | full_fare |
| ARE | 0000068 | 01770 | ACER_EVENT | 915.9000 | 8.00 | individual |
| ARE | 0000068 | 01770 | ACER_EVENT | 917.5000 | 9.00 | trip_2 |
| ARE | 0000068 | 01770 | ACER_EVENT | 923.0000 | 10.00 | Buy |
| ARE | 0000068 | 01770 | END_ITEM | 928.5000 | 11.00 | NULL |
| ARE | 0000068 | 01770 | END_ITEM | 928.5000 | 12.00 | NULL |
| ARE | 0000068 | 01770 | ACER_EVENT | 923.0000 | 13.00 | Buy |
| ARE | 0000068 | 01770 | ACER_EVENT | 917.5000 | 14.00 | trip_2 |
| ARE | 0000068 | 01770 | ACER_EVENT | 915.9000 | 15.00 | individual |
| ARE | 0000068 | 01770 | ACER_EVENT | 915.0000 | 16.00 | full_fare |
| ARE | 0000068 | 01770 | ACER_EVENT | 914.7000 | 17.00 | country_trains |
| ARE | 0000068 | 01770 | ACER_EVENT | 904.5000 | 18.00 | Cancel |
| ARE | 0000068 | 01770 | ACER_EVENT | 894.1000 | 19.00 | daily |
| ARE | 0000068 | 01770 | ACER_EVENT | 892.3000 | 20.00 | full_fare |
| ARE | 0000068 | 01770 | ACER_EVENT | 885.2000 | 21.00 | country_trains |
| Model | ||
|---|---|---|
| SRM | Realized value | |
| Discrepancy measure | ||
| 1P-ASM | Realized value | |
| Discrepancy measure | ||
| 2P-ASM | Realized value | |
| Discrepancy measure |
Table A3 Calculation Logic for Posterior Predictive p-values(ppp).
| Model | ||
|---|---|---|
| SRM | Realized value | |
| Discrepancy measure | ||
| 1P-ASM | Realized value | |
| Discrepancy measure | ||
| 2P-ASM | Realized value | |
| Discrepancy measure |
| Transition tendency parameter | Short Sequence | Long Sequence | Transition tendency parameter | Short Sequence | Long Sequence |
|---|---|---|---|---|---|
| 0.496 | 0.410 | 0.595 | 0.678 | ||
| ?0.469 | ?0.459 | 0.184 | 0.090 | ||
| 1.468 | 1.503 | ?0.217 | ?0.227 | ||
| ?0.375 | ?1.096 | 0.185 | 0.149 | ||
| ?1.091 | ?0.456 | ?1.001 | 0.965 | ||
| 0.381 | ?0.932 | 1.013 | ?1.004 | ||
| ?0.146 | 0.240 | ?0.481 | 0.522 | ||
| ?0.273 | 0.758 | 0.432 | ?0.599 | ||
| ?1.001 | ?1.481 | ?0.171 | 0.223 | ||
| 0.472 | 0.585 | 0.171 | ?0.134 | ||
| 0.451 | 0.809 | 0.028 | ?0.114 | ||
| 0.094 | 0.115 | ?0.159 | 0.431 | ||
| ?0.993 | ?1.023 | 0.071 | ?0.412 | ||
| 0.362 | 0.390 |
Table A4 The True Values of the Transition Tendency Parameter in Simulation Study.
| Transition tendency parameter | Short Sequence | Long Sequence | Transition tendency parameter | Short Sequence | Long Sequence |
|---|---|---|---|---|---|
| 0.496 | 0.410 | 0.595 | 0.678 | ||
| ?0.469 | ?0.459 | 0.184 | 0.090 | ||
| 1.468 | 1.503 | ?0.217 | ?0.227 | ||
| ?0.375 | ?1.096 | 0.185 | 0.149 | ||
| ?1.091 | ?0.456 | ?1.001 | 0.965 | ||
| 0.381 | ?0.932 | 1.013 | ?1.004 | ||
| ?0.146 | 0.240 | ?0.481 | 0.522 | ||
| ?0.273 | 0.758 | 0.432 | ?0.599 | ||
| ?1.001 | ?1.481 | ?0.171 | 0.223 | ||
| 0.472 | 0.585 | 0.171 | ?0.134 | ||
| 0.451 | 0.809 | 0.028 | ?0.114 | ||
| 0.094 | 0.115 | ?0.159 | 0.431 | ||
| ?0.993 | ?1.023 | 0.071 | ?0.412 | ||
| 0.362 | 0.390 |
| Intercept | Informative Priors | Non-informative Priors | ||||
|---|---|---|---|---|---|---|
| Mean | Standard Deviation | 95%HPD | Mean | Standard Deviation | 95%HPD | |
| 0.941 | 0.050 | (0.844, 1.038) | 0.947 | 0.049 | (0.852, 1.042) | |
| 1.613 | 0.068 | (1.484, 1.751) | 1.623 | 0.069 | (1.492, 1.758) | |
| ?1.595 | 0.063 | (?1.720, ?1.470) | ?1.603 | 0.062 | (?1.725, ?1.480) | |
| ?2.383 | 0.117 | (?2.618, ?2.161) | ?2.421 | 0.118 | (?2.650, ?2.195) | |
| ?1.344 | 0.140 | (?1.614, ?1.061) | ?1.377 | 0.143 | (?1.660, ?1.094) | |
| 0.069 | 0.168 | (?0.256, 0.396) | 0.070 | 0.170 | (?0.264, 0.404) | |
| 1.801 | 0.087 | (1.632, 1.978) | 1.820 | 0.086 | (1.654, 1.982) | |
| 0.560 | 0.115 | (0.332, 0.782) | 0.573 | 0.122 | (0.328, 0.809) | |
| ?0.214 | 0.087 | (?0.385, ?0.040) | ?0.212 | 0.087 | (?0.385, ?0.038) | |
| 0.839 | 0.154 | (0.547, 1.139) | 0.867 | 0.154 | (0.567, 1.166) | |
Table A5 Estimation Results of the Intercept Parameter for 1P-ASM under Informative/Non-Informative Priors in Simulation Study.
| Intercept | Informative Priors | Non-informative Priors | ||||
|---|---|---|---|---|---|---|
| Mean | Standard Deviation | 95%HPD | Mean | Standard Deviation | 95%HPD | |
| 0.941 | 0.050 | (0.844, 1.038) | 0.947 | 0.049 | (0.852, 1.042) | |
| 1.613 | 0.068 | (1.484, 1.751) | 1.623 | 0.069 | (1.492, 1.758) | |
| ?1.595 | 0.063 | (?1.720, ?1.470) | ?1.603 | 0.062 | (?1.725, ?1.480) | |
| ?2.383 | 0.117 | (?2.618, ?2.161) | ?2.421 | 0.118 | (?2.650, ?2.195) | |
| ?1.344 | 0.140 | (?1.614, ?1.061) | ?1.377 | 0.143 | (?1.660, ?1.094) | |
| 0.069 | 0.168 | (?0.256, 0.396) | 0.070 | 0.170 | (?0.264, 0.404) | |
| 1.801 | 0.087 | (1.632, 1.978) | 1.820 | 0.086 | (1.654, 1.982) | |
| 0.560 | 0.115 | (0.332, 0.782) | 0.573 | 0.122 | (0.328, 0.809) | |
| ?0.214 | 0.087 | (?0.385, ?0.040) | ?0.212 | 0.087 | (?0.385, ?0.038) | |
| 0.839 | 0.154 | (0.547, 1.139) | 0.867 | 0.154 | (0.567, 1.166) | |
| Intercept | Informative Priors | Non-informative Priors | ||||
|---|---|---|---|---|---|---|
| Mean | Standard Deviation | 95%HPD | Mean | Standard Deviation | 95%HPD | |
| 1.061 | 0.064 | (0.937, 1.187) | 1.069 | 0.068 | (0.937, 1.210) | |
| 1.679 | 0.084 | (1.517, 1.844) | 1.694 | 0.086 | (1.529, 1.864) | |
| ?1.910 | 0.109 | (?2.125, ?1.699) | ?1.933 | 0.113 | (?2.167, ?1.723) | |
| ?2.581 | 0.310 | (?3.220, ?2.004) | ?2.876 | 0.375 | (?3.665, ?2.197) | |
| ?1.026 | 0.305 | (?1.651, ?0.463) | ?0.987 | 0.531 | (?1.900, ?0.005) | |
| ?0.135 | 0.291 | (?0.719, 0.413) | ?0.169 | 0.331 | (?0.863, 0.454) | |
| 2.212 | 0.168 | (1.904, 2.554) | 2.288 | 0.174 | (1.967, 2.643) | |
| 1.247 | 0.247 | (0.780, 1.750) | 1.374 | 0.268 | (0.896, 1.936) | |
| ?0.139 | 0.104 | (?0.341, 0.064) | ?0.130 | 0.108 | (?0.338, 0.078) | |
| 1.238 | 0.250 | (0.772, 1.745) | 1.356 | 0.275 | (0.860, 1.933) | |
Table A6 Estimation Results of the Intercept Parameter for 2P-ASM under Informative/Non-Informative Priors in Simulation Study.
| Intercept | Informative Priors | Non-informative Priors | ||||
|---|---|---|---|---|---|---|
| Mean | Standard Deviation | 95%HPD | Mean | Standard Deviation | 95%HPD | |
| 1.061 | 0.064 | (0.937, 1.187) | 1.069 | 0.068 | (0.937, 1.210) | |
| 1.679 | 0.084 | (1.517, 1.844) | 1.694 | 0.086 | (1.529, 1.864) | |
| ?1.910 | 0.109 | (?2.125, ?1.699) | ?1.933 | 0.113 | (?2.167, ?1.723) | |
| ?2.581 | 0.310 | (?3.220, ?2.004) | ?2.876 | 0.375 | (?3.665, ?2.197) | |
| ?1.026 | 0.305 | (?1.651, ?0.463) | ?0.987 | 0.531 | (?1.900, ?0.005) | |
| ?0.135 | 0.291 | (?0.719, 0.413) | ?0.169 | 0.331 | (?0.863, 0.454) | |
| 2.212 | 0.168 | (1.904, 2.554) | 2.288 | 0.174 | (1.967, 2.643) | |
| 1.247 | 0.247 | (0.780, 1.750) | 1.374 | 0.268 | (0.896, 1.936) | |
| ?0.139 | 0.104 | (?0.341, 0.064) | ?0.130 | 0.108 | (?0.338, 0.078) | |
| 1.238 | 0.250 | (0.772, 1.745) | 1.356 | 0.275 | (0.860, 1.933) | |
| Slope | Informative Priors | Non-informative Priors | ||||
|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | Mean | Standard Deviation | |
| 2.165 | 0.145 | (1.902, 2.463) | 2.185 | 0.149 | (1.908, 2.498) | |
| 2.268 | 0.208 | (1.885, 2.703) | 2.308 | 0.213 | (1.909, 2.753) | |
| 2.075 | 0.186 | (1.736, 2.459) | 2.121 | 0.193 | (1.760, 2.510) | |
| 1.499 | 0.315 | (0.921, 2.162) | 1.772 | 0.374 | (1.102, 2.560) | |
| 0.913 | 0.298 | (0.382, 1.537) | 0.858 | 0.535 | (0.000, 1.764) | |
| 1.722 | 0.494 | (0.823, 2.764) | 1.810 | 0.562 | (0.829, 3.024) | |
| 2.125 | 0.246 | (1.655, 2.624) | 2.238 | 0.254 | (1.770, 2.758) | |
| 2.567 | 0.390 | (1.866, 3.379) | 2.764 | 0.431 | (1.978, 3.695) | |
| 2.663 | 0.282 | (2.151, 3.254) | 2.699 | 0.287 | (2.190, 3.310) | |
| 2.188 | 0.418 | (1.419, 3.045) | 2.383 | 0.466 | (1.559, 3.387) | |
Table A7 Estimation Results of the Slope Parameter for 2P-ASM under Informative/Non-Informative Priors in Simulation Study.
| Slope | Informative Priors | Non-informative Priors | ||||
|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | Mean | Standard Deviation | |
| 2.165 | 0.145 | (1.902, 2.463) | 2.185 | 0.149 | (1.908, 2.498) | |
| 2.268 | 0.208 | (1.885, 2.703) | 2.308 | 0.213 | (1.909, 2.753) | |
| 2.075 | 0.186 | (1.736, 2.459) | 2.121 | 0.193 | (1.760, 2.510) | |
| 1.499 | 0.315 | (0.921, 2.162) | 1.772 | 0.374 | (1.102, 2.560) | |
| 0.913 | 0.298 | (0.382, 1.537) | 0.858 | 0.535 | (0.000, 1.764) | |
| 1.722 | 0.494 | (0.823, 2.764) | 1.810 | 0.562 | (0.829, 3.024) | |
| 2.125 | 0.246 | (1.655, 2.624) | 2.238 | 0.254 | (1.770, 2.758) | |
| 2.567 | 0.390 | (1.866, 3.379) | 2.764 | 0.431 | (1.978, 3.695) | |
| 2.663 | 0.282 | (2.151, 3.254) | 2.699 | 0.287 | (2.190, 3.310) | |
| 2.188 | 0.418 | (1.419, 3.045) | 2.383 | 0.466 | (1.559, 3.387) | |
| Transition tendency parameter | Mean | Standard Deviation | 95%HPD | Transition tendency parameter | Mean | Standard Deviation | 95%HPD |
|---|---|---|---|---|---|---|---|
| 0.587 | 0.035 | (0.519, 0.656) | ?0.886 | 0.107 | (?1.101, ?0.677) | ||
| ?0.587 | 0.035 | (?0.656, ?0.519) | 0.790 | 0.136 | (0.523, 1.067) | ||
| 1.740 | 0.068 | (1.608, 1.873) | 0.052 | 0.127 | (?0.201, 0.308) | ||
| ?0.003 | 0.065 | (?0.129, 0.125) | ?0.843 | 0.157 | (?1.153, ?0.542) | ||
| ?1.737 | 0.097 | (?1.935, ?1.554) | ?0.680 | 0.064 | (?0.805, ?0.557) | ||
| 1.586 | 0.075 | (1.443, 1.738) | 0.680 | 0.064 | (0.557, 0.805) | ||
| 0.165 | 0.076 | (0.011, 0.320) | ?0.761 | 0.064 | (?0.886, ?0.635) | ||
| ?1.751 | 0.120 | (?1.998, ?1.523) | 0.761 | 0.064 | (0.635, 0.886) | ||
| 1.785 | 0.082 | (1.625, 1.946) | 0.373 | 0.064 | (0.247, 0.503) | ||
| ?0.049 | 0.094 | (?0.231, 0.132) | ?0.666 | 0.054 | (?0.773, ?0.560) | ||
| ?1.372 | 0.153 | (?1.688, ?1.086) | 0.293 | 0.045 | (0.207, 0.381) | ||
| ?0.364 | 0.105 | (?0.576, ?0.163) | 0.171 | 0.089 | (?0.007, 0.345) | ||
| 1.589 | 0.079 | (1.433, 1.744) | ?0.171 | 0.089 | (?0.345, 0.007) | ||
| ?0.702 | 0.099 | (?0.897, ?0.513) |
Table A8 Parameter Estimation Results of SRM in Empirical Research.
| Transition tendency parameter | Mean | Standard Deviation | 95%HPD | Transition tendency parameter | Mean | Standard Deviation | 95%HPD |
|---|---|---|---|---|---|---|---|
| 0.587 | 0.035 | (0.519, 0.656) | ?0.886 | 0.107 | (?1.101, ?0.677) | ||
| ?0.587 | 0.035 | (?0.656, ?0.519) | 0.790 | 0.136 | (0.523, 1.067) | ||
| 1.740 | 0.068 | (1.608, 1.873) | 0.052 | 0.127 | (?0.201, 0.308) | ||
| ?0.003 | 0.065 | (?0.129, 0.125) | ?0.843 | 0.157 | (?1.153, ?0.542) | ||
| ?1.737 | 0.097 | (?1.935, ?1.554) | ?0.680 | 0.064 | (?0.805, ?0.557) | ||
| 1.586 | 0.075 | (1.443, 1.738) | 0.680 | 0.064 | (0.557, 0.805) | ||
| 0.165 | 0.076 | (0.011, 0.320) | ?0.761 | 0.064 | (?0.886, ?0.635) | ||
| ?1.751 | 0.120 | (?1.998, ?1.523) | 0.761 | 0.064 | (0.635, 0.886) | ||
| 1.785 | 0.082 | (1.625, 1.946) | 0.373 | 0.064 | (0.247, 0.503) | ||
| ?0.049 | 0.094 | (?0.231, 0.132) | ?0.666 | 0.054 | (?0.773, ?0.560) | ||
| ?1.372 | 0.153 | (?1.688, ?1.086) | 0.293 | 0.045 | (0.207, 0.381) | ||
| ?0.364 | 0.105 | (?0.576, ?0.163) | 0.171 | 0.089 | (?0.007, 0.345) | ||
| 1.589 | 0.079 | (1.433, 1.744) | ?0.171 | 0.089 | (?0.345, 0.007) | ||
| ?0.702 | 0.099 | (?0.897, ?0.513) |
| [1] |
Arieli-Attali M., Ou L., & Simmering V. R. (2019). Understanding test takers' choices in a self-adapted test: A hidden Markov modeling of process data. Frontiers in Psychology, 10, 83.
doi: 10.3389/fpsyg.2019.00083 pmid: 30787889 |
| [2] |
Beck L. W. (1943). The principle of parsimony in empirical science. The Journal of Philosophy, 40(23), 617-633. https://doi.org/10.2307/2019692
doi: 10.2307/2019692 URL |
| [3] | Bergner Y., Walker E., & Ogan A. (2017). Dynamic Bayesian network models for peer tutoring interactions. In A. A. von Davier, M. Zhu, & P. C. Kyllonen (Eds), Innovative assessment of collaboration (pp. 249-268). Cham: Springer. |
| [4] | Birnbaum A. (1968). Some latent trait models and their use in inferring an examinee's ability. In F. M. Lord & M. R. Novick (Eds.), Statistical theories of mental test scores (pp.397-124). Reading, MA: Addison-Wesley. |
| [5] |
Bock R. D. (1972). Estimating item parameters and latent ability when responses are scored in two or more nominal categories. Psychometrika, 37(1), 29-51. https://doi.org/10.1007/BF02291411
doi: 10.1007/BF02291411 URL |
| [6] |
Buchner A., & Funke J. (1993). Finite-state automata: Dynamic task environments in problem-solving research. The Quarterly Journal of Experimental Psychology, 46(1), 83-118.
doi: 10.1080/14640749308401068 URL |
| [7] |
Chen Y. (2020). A continuous-time dynamic choice measurement model for problem-solving process data. Psychometrika, 85(4), 1052-1075.
doi: 10.1007/s11336-020-09734-1 pmid: 33346883 |
| [8] | Fu Y., Zhan P., Chen Q., & Jiao H. (2022). Joint modeling of action sequences and action times in problem-solving tasks. PsyArXiv. Retrieved from psyarxiv.com/e3nbc |
| [9] | Gelman A., Meng X.-L., & Stern H. (1996). Posterior predictive assessment of model fitness via realized discrepancies. Statistica Sinica, 6, 733-760. |
| [10] | Gelman A., & Rubin D. B. (1992). Inference from iterative simulation using multiple sequences. Statistical Science, 7, 457-511. |
| [11] |
Han Y., Liu H., & Ji F. (2022). A sequential response model for analyzing process data on technology-based problem-solving tasks. Multivariate Behavioral Research, 57(6), 960-977.
doi: 10.1080/00273171.2021.1932403 URL |
| [12] |
Han Y., & Wilson M. (2022). Analyzing student response processes to evaluate success on a technology-based problem-solving task. Applied Measurement in Education, 35(1), 33-45.
doi: 10.1080/08957347.2022.2034821 URL |
| [13] |
Han Y., Xiao Y., & Liu H. (2022). Feature extraction and ability estimation of process data in the problem-solving test. Advances in Psychological Science, 30(6), 1393-1409.
doi: 10.3724/SP.J.1042.2022.01393 |
| [14] | Hao J., Shu Z., & von Davier A. (2015). Analyzing process data from game/scenario-based tasks: An edit distance approach. Journal of Educational Data Mining, 7(1), 33-50. |
| [15] | Harding S. M. E., Griffin P. E., Awwal N., Alom B. M., & Scoular C. (2017). Measuring collaborative problem solving using mathematics-based tasks. AERA Open, 3(3), 1-19. |
| [16] |
He Q., Borgonovi F., & Paccagnella M. (2021). Leveraging process data to assess adults’ problem-solving skills: Using sequence mining to identify behavioral patterns across digital tasks. Computers & Education, 166, 104170.
doi: 10.1016/j.compedu.2021.104170 URL |
| [17] | He Q., & von Davier M. (2016). Analyzing process data from problem-solving items with N-grams:Insights from a computer-based large-scale assessment. In R. Yigal, F. Steve, & M. Maryam (Eds.), Handbook of research on technology tools for real-world skill development (pp. 749-776). Hershey, PA: Information Science Reference. |
| [18] | Hoffman M. D., & Gelman A. (2014). The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. Journal of Machine Learning Research, 15(1), 1593-1623. |
| [19] |
LaMar M. M. (2018). Markov decision process measurement model. Psychometrika, 83(1), 67-88.
doi: 10.1007/s11336-017-9570-0 pmid: 28447309 |
| [20] |
Levy R. (2019). Dynamic Bayesian network modeling of game-based diagnostic assessments. Multivariate Behavioral Research, 54(6), 771-794.
doi: 10.1080/00273171.2019.1590794 pmid: 30942094 |
| [21] |
Li M., Liu Y., Liu H. (2020). Analysis of the Problem-solving strategies in computer-based dynamic assessment: The extension and application of multilevel mixture IRT model. Acta Psychologica Sinica, 52(4), 528-540.
doi: 10.3724/SP.J.1041.2020.00528 |
| [22] |
Liu H., Liu Y., & Li M. (2018). Analysis of process data of PISA 2012 computer-based problem solving: Application of the modified multilevel mixture IRT model. Frontiers in Psychology, 9, 1372.
doi: 10.3389/fpsyg.2018.01372 pmid: 30123171 |
| [23] |
Liu Y., Xu H., Chen Q., & Zhan P. (2022). The measurement of problem-solving competence using process data. Advances in Psychological Science, 30(3), 522-535.
doi: 10.3724/SP.J.1042.2022.00522 |
| [24] |
Ma W., Iaconangelo C., & de la Torre J. (2016). Model similarity, model selection, and attribute classification. Applied Psychological Measurement, 40(3), 200-217.
doi: 10.1177/0146621615621717 pmid: 29881048 |
| [25] |
Man K., Harring J. R., & Zhan P. (2022). Bridging models of biometric and psychometric assessment: A three-way joint modeling approach of item responses, response times and gaze fixation counts. Applied Psychological Measurement, 46(5), 361-381.
doi: 10.1177/01466216221089344 URL |
| [26] | Newell A., & Simon H. A. (1972). Human problem solving (Vol. 104, No. 9). Englewood Cliffs. |
| [27] | OECD. (2013). PISA 2012 assessment and analytical framework: Mathematics, reading, science, problem solving and financial literacy. OECD Publishing. http://dx.doi.org/10.1787/9789264190511-en |
| [28] |
Peng S., Cai Y., Wang D., Luo F., & Tu D. (2022). A generalized diagnostic classification modeling framework integrating differential speediness: Advantages and illustrations in psychological and educational testing. Multivariate Behavioral Research, 57(6), 940-959.
doi: 10.1080/00273171.2021.1928474 URL |
| [29] | Rasch G. (1960). On general laws and the meaning of measurement in psychology. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability: Held at the Statistical Laboratory, University of California, June 20-July 30, 1960 (Vol. 4, pp. 321). University of California Press. |
| [30] |
Rosen Y. (2017). Assessing students in human‐to‐agent settings to inform collaborative problem‐solving learning. Journal of Educational Measurement, 54(1), 36-53.
doi: 10.1111/jedm.2017.54.issue-1 URL |
| [31] | Shu Z., Bergner Y., Zhu M., Hao J., & von Davier A. A. (2017). An item response theory analysis of problem-solving processes in scenario-based tasks. Psychological Test and Assessment Modeling, 59(1), 109-131. |
| [32] |
Tang X., Wang Z., He Q., Liu J., & Ying Z. (2020). Latent feature extraction for process data via multidimensional scaling. Psychometrika, 85(2), 378-397.
doi: 10.1007/s11336-020-09708-3 pmid: 32572672 |
| [33] | Tang X., Wang Z., Liu J., & Ying Z. (2021). An exploratory analysis of the latent structure of process data via action sequence autoencoders. British Journal of Mathematical and Statistical Psychology, 74(1), 1-33. |
| [34] | van der Linden W. J. (2006). A lognormal model for response times on test items. Journal of Educational and Behavioral Statistics, 31(2), 181-204. |
| [35] |
van der Linden W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items. Psychometrika, 72(3), 287-308.
doi: 10.1007/s11336-006-1478-z URL |
| [36] |
Vehtari A., Gelman A., & Gabry J. (2017). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing, 27, 1413-1432.
doi: 10.1007/s11222-016-9696-4 |
| [37] |
Vista A., Care E., & Awwal N. (2017). Visualising and examining sequential actions as behavioural paths that can be interpreted as markers of complex behaviours. Computers in Human Behavior, 76, 656-671.
doi: 10.1016/j.chb.2017.01.027 URL |
| [38] | Watanabe S. (2010). Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. Journal of Machine Learning Research, 11(12), 3571-3594. |
| [39] |
Wilson M., Gochyyev P., & Scalise K. (2017). Modeling data from collaborative assessments: learning in digital interactive social networks. Journal of Educational Measurement, 54(1), 85-102.
doi: 10.1111/jedm.2017.54.issue-1 URL |
| [40] |
Xiao Y., He Q., Veldkamp B., & Liu H. (2021). Exploring latent states of problem‐solving competence using hidden Markov model on process data. Journal of Computer Assisted Learning, 37(5), 1232-1247.
doi: 10.1111/jcal.v37.5 URL |
| [41] | Xiao Y., & Liu H. (2023). A state response measurement model for problem-solving process data. Behavior Research Methods, Online First. |
| [42] |
Yuan J., Xiao Y., & Liu H. (2019). Assessment of collaborative problem solving based on process stream data: A new paradigm for extracting indicators and modeling dyad data. Frontiers in Psychology, 10, 369.
doi: 10.3389/fpsyg.2019.00369 pmid: 30863344 |
| [43] |
Zhan P., Jiao H., & Liao D. (2018). Cognitive diagnosis modelling incorporating item response times. British Journal of Mathematical and Statistical Psychology, 71(2), 262-286.
doi: 10.1111/bmsp.2018.71.issue-2 URL |
| [44] | Zhan P., Man K., Wind S. A., & Malone J. (2022). Cognitive diagnosis modeling incorporating response times and fixation counts: Providing comprehensive feedback and accurate diagnosis. Journal of Educational and Behavioral Statistics, 47(6), 736-776. |
| [45] |
Zhan P., & Qiao X. (2022). Diagnostic classification analysis of problem-solving competence using process data: An item expansion method. Psychometrika, 87(4), 1529-1547.
doi: 10.1007/s11336-022-09855-9 pmid: 35389193 |
| [46] | Zhan S., Hao J., & Davier A. V. (2015). Analyzing process data from game/scenariobased tasks: An edit distance approach. Journal of Educational Data Mining, 7(1), 33-50. |
| [47] |
Zhang S., Wang Z., Qi J., Liu J., & Ying Z. (2022). Accurate assessment via process data. Psychometrika, 88(1), 76-97.
doi: 10.1007/s11336-022-09880-8 pmid: 35962849 |
| [48] |
Zhu M., Shu Z., & von Davier A. A. (2016). Using networks to visualize and analyze process data for educational assessment. Journal of Educational Measurement, 53(2), 190-211.
doi: 10.1111/jedm.12107 URL |
| [1] | TONG Hao, YU Xiaofeng, QIN Chunying, PENG Yafeng, ZHONG Xiaoyuan. Detection of aberrant response patterns using a residual-based statistic in testing with polytomous items [J]. Acta Psychologica Sinica, 2022, 54(9): 1122-1136. |
| [2] | REN He, CHEN Ping. Two new termination rules for multidimensional computerized classification testing [J]. Acta Psychologica Sinica, 2021, 53(9): 1044-1058. |
| [3] | ZHAN Peida, JIAO Hong, MAN Kaiwen. The multidimensional log-normal response time model: An exploration of the multidimensionality of latent processing speed [J]. Acta Psychologica Sinica, 2020, 52(9): 1132-1142. |
| [4] | LI Meijuan,LIU Yue,LIU Hongyun. Analysis of the Problem-solving strategies in computer-based dynamic assessment: The extension and application of multilevel mixture IRT model [J]. Acta Psychologica Sinica, 2020, 52(4): 528-540. |
| [5] | LIU Yue, LIU Hongyun. Reporting overall scores and domain scores of bi-factor models [J]. Acta Psychologica Sinica, 2017, 49(9): 1234-1246. |
| [6] | CHEN Ping. Two new online calibration methods for computerized adaptive testing [J]. Acta Psychologica Sinica, 2016, 48(9): 1184-1198. |
| [7] | MENG Xiangbin; TAO Jian; CHEN Shali. Warm’sweighted maximum likelihood estimation of latent trait in the four-parameter logistic model [J]. Acta Psychologica Sinica, 2016, 48(8): 1047-1056. |
| [8] | WANG Wenyi;SONG Lihong;DING Shuliang. Classification accuracy and consistency indices for complex decision rules in multidimensional item response theory [J]. Acta Psychologica Sinica, 2016, 48(12): 1612-1624. |
| [9] | ZHAN Peida; CHEN Ping; BIAN Yufang. Using confirmatory compensatory multidimensional IRT models to do cognitive diagnosis [J]. Acta Psychologica Sinica, 2016, 48(10): 1347-1356. |
| [10] | ZHAN Peida; LI Xiaomin; WANG Wen-Chung; BIAN Yufang; WANG Lijun. The Multidimensional Testlet-Effect Cognitive Diagnostic Models [J]. Acta Psychologica Sinica, 2015, 47(5): 689-701. |
| [11] | YAO Ruosong;ZHAO Baonan;LIU Ze;MIAO Qunying. The Application of Many-Facet Rasch Model in Leaderless Group Discussion [J]. Acta Psychologica Sinica, 2013, 45(9): 1039-1049. |
| [12] | LIU Yue;LIU Hongyun. Comparison of MIRT Linking Methods for Different Common Item Designs [J]. Acta Psychologica Sinica, 2013, 45(4): 466-480 . |
| [13] | DU Wenjiu;ZHOU Juan;LI Hongbo. The Item Parameters’ Estimation Accuracy of Two-Parameter Logistic Model [J]. Acta Psychologica Sinica, 2013, 45(10): 1179-1186. |
| [14] | LIU Hong-Yun,LI Chong,ZHANG Ping-Ping,LUO Fang. Testing Measurement Equivalence of Categorical Items’ Threshold/Difficulty Parameters: A Comparison of CCFA and (M)IRT Approaches [J]. Acta Psychologica Sinica, 2012, 44(8): 1124-1136. |
| [15] | LIU Hong-Yun,LUO Fang,WANG Yue,ZHANG Yu. Item Parameter Estimation for Multidimensional Measurement: Comparisons of SEM and MIRT Based Methods [J]. , 2012, 44(1): 121-132. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||