1 引言
早期的决策研究大都遵循个体完全理性的理论假设, 认为人们的决策是追求自我利益的最大化。在这种早期“经典”理论的影响之下, Savage (1954)提出了确定事件(sure-thing principle)原则, 所谓确定事件原则是指如果决策者知道事件E会发生, 他会采取行动A; 如果决策者知道事件E不会发生, 他仍会采取行动A; 以此观之, 决策者在不知道事件E是否会发生的情况下, 也会采取行动A。然而, 大量研究表明, 决策者并非总是遵循这一原则, 即当决策者不知道事件E是否会发生的情况下, 他会拒绝行动A, 这一现象被称为分离效应(Tversky & Shafir, 1992; 汪祚军, 李纾, 2008)。
一系列的研究已经证实, 在一次性二人囚徒困境博弈中, 决策者的行为往往也会违背确定事件原则, 出现分离效应(Busemeyer, Matthew, & Wang, 2006; Croson, 1999; Li & Taplin, 2002; Tversky & Shafir, 1992)。在这一博弈中, 只有合作和背叛两种策略可供博弈双方选择。无论对方选择合作还是背叛, 当自己选择背叛时, 收益是最大的(标准囚徒困境博弈中的收益矩阵如表1所示, 其中πc > πd > πa > πb) (Denolf, Martínez, Josephy, & Duran, 2017; Smith, 1982), 因此选择背叛是决策双方的优势策略。根据确定事件原则, 在对方策略不明的情况下, 决策者做出背叛的可能性应该介于两种确定的状态(对方背叛、对方合作)下决策者背叛的可能性之间。但实验结果表明, 此时决策者背叛的可能性小于两种确定状态下决策者背叛的可能性, 即出现了分离效应。例如, 在Shafir和Tversky (1992)的研究中, 在两种确定情况下(已知对手背叛/合作), 决策者选择背叛的概率分别为97%和84%, 而在对手决策未知这一情况下, 决策者选择背叛的概率却只有63%。
近10年来, 一些学者基于量子理论研究思想与方法探索出了量子决策模型, 为解释诸如分离效应这样违背传统决策理论的现象提供了新思路。量子决策模型能够给出独立于模型的参数和实证数据的预测, 且针对不同研究问题所构建模型的表述形式也不尽相同(Blutner, Pothos, & Bruza, 2013; Bruza, Wang, & Busemeyer, 2015; Busemeyer & Wang, 2015; Busemeyer, Wang, Khrennikov, & Basieva, 2014; 辛潇洋, 徐晨虹, 陈宏玉, 李瑛, 2018)。其中, 针对囚徒困境中出现的分离效应, Pothos和Busemeyer借鉴认知失调理论构建了可以解释囚徒困境中分离效应的四维动态量子决策模型(Pothos & Busemeyer, 2009; Busemeyer & Bruza, 2012)。但是, 当前量子决策模型在解释囚徒困境时, 仍存在一些困难之处。接下来, 本文将首先指出并分析这些困难, 并在此基础上, 提出解决这些困难的方法。
2 当前量子决策模型的困难
由Jerome R. Busemeyer教授等人提出的, 用以解释囚徒困境博弈中的分离效应的四维量子决策模型是一种较为成熟的动态量子决策模型, 这种模型及其变式可用来解释两阶段赌博任务中的分离效应以及分类-决策中的干涉效应等违背传统决策模型的现象(Busemeyer, Wang, & Lambert-Mogiliansky, 2009; Pothos & Busemeyer, 2009; Busemeyer & Bruza, 2012; Busemeyer, Wang, & Pothos, 2015; Wang & Busemeyer, 2016)。然而, 这种模型在对囚徒困境中分离效应进行分析解释的过程中, 存在着一些困难, 接下来, 本文将指出这些困难, 并分析产生这些困难的原因。
2.1 四维标准量子决策模型
研究者首先试图通过一种四维标准量子决策模型来解释囚徒困境博弈中的分离效应。在这一模型中, 首先需要定义研究问题的空间, 这一空间是对决策者所有可能出现的信念行为状态的界定, 在囚徒困境博弈中, 问题空间包含四种决策者可能报告的基态(basis state), 分别为${{\text{B}}_{D}}{{\text{A}}_{D}},{{\text{B}}_{D}}{{\text{A}}_{C}},{{\text{B}}_{C}}{{\text{A}}_{D}},$ ${{\text{B}}_{C}}{{\text{A}}_{C}}$。其中, BiAj表示决策者认为对方会采取i行动的信念状态(Belief state), 但其自身决定采取j行动的行为状态(Action state) ($i,j\in \{\text{C},\text{D}\}$, D表示背叛, C表示合作)。问题空间中共有四个“维度”, 所以这种模型称为“四维”模型, 且四个维度是互斥的, 代表了决策者所有可能出现的确定的信念与行为, 从数学上来说, 这个问题空间称为希尔伯特空间, 而这四个“维度”对应于这一空间的四个基矢(苏汝铿, 2002)。据此, 决策者的信念行为状态可由一个4×1列向量表示:
这样的状态在量子力学中称为叠加态, 在进行观测(或者从心理学的角度, 在要求被试报告决策结果)时,概率振幅$\psi_{ij}$ 模的平方$|{{\psi }_{ij}}{{|}^{2}}$即表示决策者从叠加态转变为基态${{\text{B}}_{i}}{{\text{A}}_{j}}$的概率, 且$\underset{i}{\mathop \sum }\,\underset{j}{\mathop \sum }\,|{{\psi }_{ij}}{{|}^{2}}=1$,以满足状态的归一性。设定在未知对手策略的情况下, 决策者初始信念行为状态为:
根据上文所述, 这一状态中, 在要求被试报告决策结果时, 从这一量子叠加态转变为任意一种基态的概率是相等的, 都为(1/2)2 = 0.25。当已知对方策略为背叛时, 决策者便不可能报告${{\text{B}}_{C}}{{\text{A}}_{D}}$和${{\text{B}}_{C}}{{\text{A}}_{C}}$, 此时${{\psi }_{CD}}={{\psi }_{CC}}=0$, 可令其转变为其他两种基态的可能性相同, 那么, 决策者在此时的初始状态可表示为${{\psi }_{1}}(0)={{[\sqrt{2}/2,\sqrt{2}/2,0,0]}^{T}}$, 此时决策者报告${{\text{B}}_{D}}{{\text{A}}_{D}}$和${{\text{B}}_{D}}{{\text{A}}_{C}}$的概率均为${{(\sqrt{2}/2)}^{2}}=1/2$。同理, 当决策者已知对手选择合作时, 其初始信念与行为状态可表示为${{\psi }_{2}}(0)={{[0,0,\sqrt{2}/2,\sqrt{2}/2]}^{T}}$ 。
根据量子决策模型, 决策者的信念行为状态会依据收益矩阵动态地从初始状态$\psi (0)$转变为最终状态$\psi (t)$, 而这种动态过程, 可以用薛定谔方程$i\cdot (d\psi /dt)={{\text{H}}_{\text{A}}}\cdot \psi $的解$\psi (t)={{e}^{-it{{\text{H}}_{\text{A}}}}}\cdot \psi (0)$描述1( 在量子决策模型中, 通常将薛定谔方程中的普朗克常数h设定为1。方程中, i表示虚数单位, e表示自然常数, t表示决策过程所需的时间, 但并非客观的绝对时间。)。矩阵$U(t)={{e}^{-it{{\text{H}}_{\text{A}}}}}$为酉矩阵(Unitary Matrix), 其中第i行第j列元素的模的平方$|{{U}_{ij}}(t){{|}^{2}}$表示在时间t内从状态j转变为状态i的概率。该矩阵满足${{U}^{\dagger }}U=$ ${{U}^{\dagger }}U=I$, 以保证状态ψ的内积不变, 从而确保决策者在决策时转变为所有可能基态概率之和保持为1。在薛定谔方程中, 哈密顿矩阵(Hamiltonian Matrix) HA起着至关重要的作用, 在这一模型中, 哈密顿矩阵仅根据决策者自身的收益矩阵建立, 故而称之为“标准”模型, 其哈密顿矩阵如式(3)所示:
其中的参数${{u}_{d}}$和${{u}_{c}}$是与不同决策条件下决策者收益之差有关的效用函数, 其取值范围在-1到1之间。${{u}_{d}}=u({{x}_{DD}}-{{x}_{DC}}),{{u}_{c}}=u({{x}_{CD}}-{{x}_{CC}}),{{x}_{ij}}$表示当对手的行动为i, 决策者的行动为j时决策者的收益。例如${{x}_{DD}}$表示当对手选择背叛(D), 决策者也选择背叛时(D), 决策者的收益为${{\pi }_{a}}$, 所以${{x}_{DD}}={{\pi }_{a}}$, 同理可知${{x}_{DC}}={{\pi }_{b}},{{x}_{CD}}={{\pi }_{c}},{{x}_{CC}}={{\pi }_{d}}$, 据此${{u}_{d}}=$ $u({{\pi }_{a}}-{{\pi }_{b}}),{{u}_{c}}=u({{\pi }_{c}}-{{\pi }_{d}})$, 而根据Shafir和Tversky (1992)研究中的收益矩阵, 此时${{\pi }_{a}}=10,{{\pi }_{b}}=5,{{\pi }_{c}}=$ $25,{{\pi }_{d}}=20$, 因此有${{u}_{d}}={{u}_{c}}=u(5)=u$。依此将${{\psi }_{0}},{{\psi }_{1}},$ ${{\psi }_{2}}$代入薛定谔方程, 便可得到不同条件下决策者经过时间t后形成的最终信念与行为状态${{\psi }_{0}}(t),$ ${{\psi }_{1}}(t),{{\psi }_{2}}(t)$, 通过计算最终状态中背叛行为概率之和, 即式(1)第一行元素模的平方与第三行元素模平方之和$(|{{\psi }_{DD}}{{|}^{2}}+|{{\psi }_{CD}}{{|}^{2}})$, 便可以得出不同条件下决策者决策时从最终信念行为状态转变为${{\text{B}}_{D}}{{\text{A}}_{D}}$和${{\text{B}}_{C}}{{\text{A}}_{D}}$的概率之和, 即决策者选择背叛的概率。但是, 计算得出决策者在三种条件下做出背叛行为的概率相同, 说明四维标准量子模型无法解释一次性两人囚徒困境博弈中的分离效应(Pothos & Busemeyer, 2009; Busemeyer & Bruza, 2012), 这便是四维标准量子模型的困难。
2.2 Pothos和Busemeyer (2009)对四维标准量子决策模型的改进
Pothos和Busemeyer (2009)认为, 决策者在决策过程中会产生认知失调, Wang和Busemeyer (2016)后来将其称为信念与行为的纠缠(belief-action entanglement), Shafir和Tversky (1992)则把这种个人的偏见表述为“一厢情愿”(wishful thinking), 即当决策者认为对手的策略为合作/背叛时, 他倾向于采取同样的行动(Festinger, 1957), 这种信念与行动间的关系可由式(4)所示的矩阵表示:
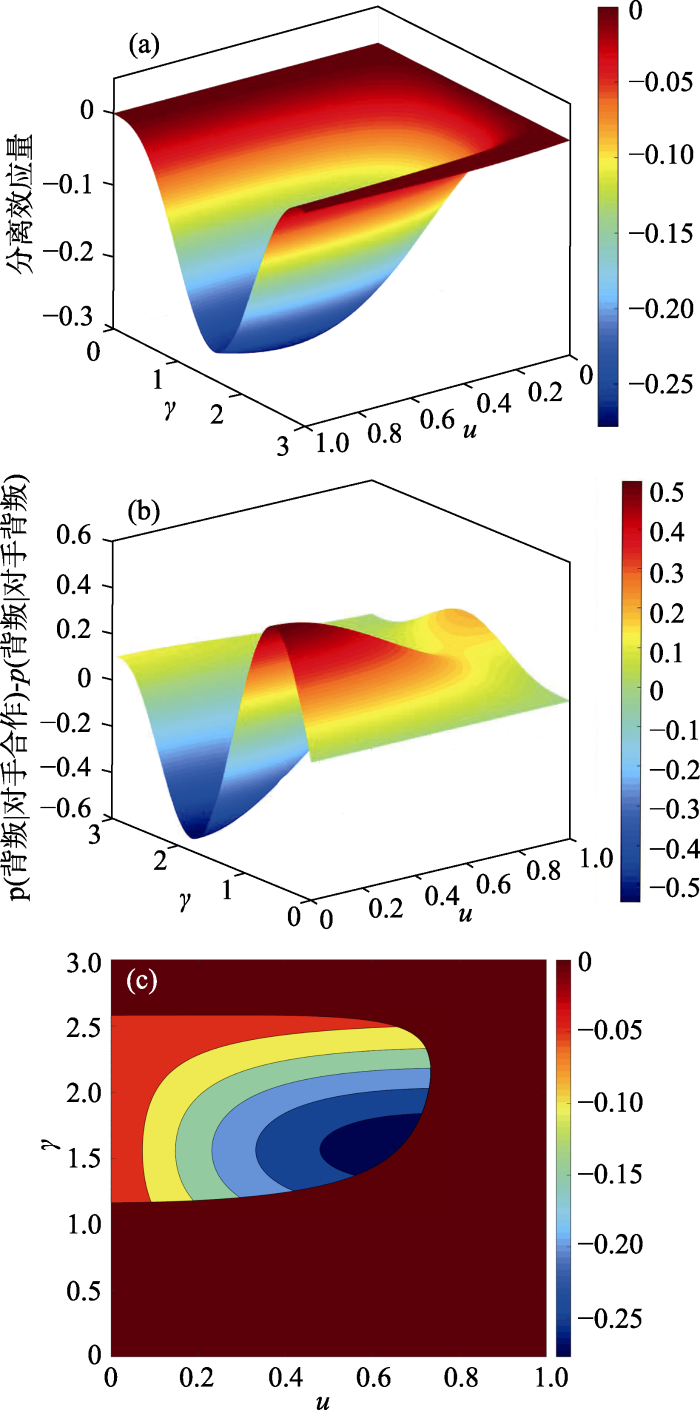
Pothos和Busemeyer将认知失调矩阵加入薛定谔方程中, 构建出新的哈密顿矩阵${{H}_{C}}={{H}_{A}}+{{H}_{B}}$ 代入薛定谔方程, 并据此计算出决策者在不同条件下背叛的概率, 进而对囚徒困境中的分离效应进行解释。为了更直观地展示, 本文使用Matlab的3D绘图技术绘制出分离效应量1( 仿照Pothos和Busemeyer (2009)中的图1, 将分离效应量定义为决策者在不确定条件下选择背叛的概率减去两种确定情况下选择背叛概率的平均值, 即:$p(背叛)-\frac{1}{2}(p(背叛|对手合作)+p(背叛|对手背叛))$。)以及p (背叛│对手合作) - p (背叛│对手背叛)与模型参数u (效用函数, 其值越大, 表示决策者的收益之差越大)和γ (信念与行为的纠缠的参数, 其值越大, 表示在相同时间内, 这种纠缠的程度越大)之间的关系, 如图1所示。从图1(a)中可以看出, 当u和γ在一定的范围内取值时, 模型便会产生明显的分离效应量(即图中冷色部分), 这样囚徒困境中的分离效应便得以解释。
图1
图1
Pothos和Busemeyer (2009)量子决策模型中分离效应量以及p(背叛│对手合作) - p(背叛│对手背叛)与u和γ之间关系的3D着色表面图(a-b)与有效区域的着色等高线图(c) (其中t =π/2 )
表2 不同研究中决策者选择背叛的概率以及不同量子决策模型的拟合结果
| 研究 | 已知对手背叛 | 已知对手合作 | 对手策略未知 | 绝对误差 |
|---|---|---|---|---|
| Shafir & Tversky (1992) | 0.97 (0.79/0.95) | 0.84 (0.77/0.84) | 0.63 (0.63/0.65) | 0.25/0.04 |
| Li & Taplan (2002) | 0.73 (0.73/0.77) | 0.67 (0.67/0.66) | 0.60 (0.67/0.55) | 0.07/0.09 |
| Busemeyer et al. (2006) | 0.91 (0.80/0.91) | 0.84 (0.78/0.84) | 0.66 (0.66/0.63) | 0.17/0.02 |
| 平均值 | 0.87 (0.79/0.87) | 0.78 (0.78/0.78) | 0.63 (0.63/0.60) | 0.08/0.03 |
注:括号内为先前的量子模型拟合结果/本研究提出的量子模型的拟合结果
若我们继续探究的话, 便会发现这一模型的第三个困难, 即无法解释决策者自身收益之差的效用函数u与分离效应量之间的关系。已有的研究已经证实, 当决策者的收益之差增大时, 会导致分离效应的减少(Li & Taplin, 2002; 李纾, 2016)。而从图1(c)中可以看出, 当u增大时, 分离效应量的绝对值反而呈现增加的趋势。
Pothos和Busemeyer (2009)提出的改进模型在解释囚徒困境中的分离效应时仍存在困难, 究其原因, 主要有两点:一是决策者在不同决策条件下所参考的收益维度是不同的——决策者不仅考虑自己维度上的收益, 也可能在一定情况下考虑对方维度上的收益情况(Li & Taplin, 2002; 李纾, 2016), 而在四维标准量子模型中, 不同条件下薛定谔方程中哈密顿矩阵中所使用的效用函数都是基于决策者自身的收益维度的, 说明该模型并没有反映出决策者在不同决策条件下的差别; 二是效用函数${{u}_{d}}$和${{u}_{c}}$的计算过度简化, 实际上两者并不一定相等(Kahneman & Tversky, 2013; Blanco, Engelmann, Koch, & Normann, 2014)。若从预期理论(prospect theory)的角度来看, ${{u}_{d}}=~u({{x}_{DD}})-u({{x}_{DC}})=u(10)-u(5)$, 而${{u}_{c}}=u({{x}_{CD}})-u({{x}_{CC}})=u(25)-u(20) $, 由于效用函数一般是非线性的(Pleskac, Diederich, & Wallsten, 2015; Tversky & Kahneman, 1981), 此时${{u}_{d}}$是不等于${{u}_{c}}$的, 因此原先模型中关于效用函数的设定是不严谨的。本文的目标便是基于上述分析, 对四维量子决策模型进行改进。改进的重点与难点在于, 如何确定不同决策条件下决策者所参考的收益, 进而确定.不同条件下表征收益的哈密顿矩阵HA, 而齐当别思想恰好提供了解决这一问题的思路。
3 一种齐当别思想下的量子决策模型
3.1 齐当别模型对囚徒困境中分离效应的解释
齐当别模型认为, 左右人类风险决策行为的机制不是最大限度地追求某种形式的期望值, 而是某种形式上辨察选择对象之间是否存在“优势性”关系, 并借助最好可能结果和最坏可能结果对问题进行表征。人们必须在一个或几个维度上将差别较小的可能结果人为地“齐同”掉, 而在差别较大的维度上选择出具有优势的选项(Li & Taplin, 2002; 毕研玲, 李纾, 2007; 李纾, 2005; 李纾等, 2009)。因此, 该模型认为, 在一次性标准囚徒困境实验中, 决策者在不同条件下决策所基于的“维度”是不同的。在两种确定条件下, 由于在“自己收益维度”上, 背叛明显优于合作, 因此决策者倾向于将“他人收益维度”上的差异“齐同”掉, 从而在“自己收益维度”上做决策, 选择对自己有利的行为(背叛); 而在不确定条件下, 由于在“自己收益维度”上, 背叛策略不再明显地优于合作策略, 而在“他人收益维度”上, 合作策略明显优于背叛策略, 这样, 决策者抑或倾向于将“自己收益维度”上的差异“齐同”掉, 而在“他人收益维度”上做决策, 选择对他人有利的行为(合作) (Li & Taplin, 2002; 李纾, 2016; 汪祚军, 李纾, 2008)。
据此可知, 当决策者处于两种对手策略确定的情况时, 他是基于自己的收益做决策的, 此时量子决策模型中的哈密顿矩阵可根据决策者自身维度上的效用函数进行定义。当决策者处于不确定的决策条件时(对手策略未知), 若决策者只处于“他人收益维度”上, 那么选择合作便是这一维度上的占优选项, 此时决策者选择合作的概率应大于选择背叛的概率, 而这与实际研究结果却不相符。以此观之, 此时决策者应该既考虑自己的收益, 又兼顾他人的收益, 因此, 在对手策略未知的情况下, 哈密顿矩阵需要根据决策者以及他人的效用函数进行定义。接下来, 本文将基于以上分析对量子决策模型进行修正与重构。
3.2 齐当别思想下量子决策模型的重构
3.2.1 确定条件下哈密顿矩阵的修正
首先, 在已知对手策略为背叛时, 决策者是基于“自己收益维度”做出决策的, 即在这种情况下决策者是以自己收益的效用函数为基准的。因此, 此时哈密顿矩阵可用${{u}_{d}}$表示决策者在知道对手背叛的条件下, 做出背叛行为和做出合作行为自身所获收益效用之差。但是, 由于此时决策者已经认为对手采取背叛策略, 所以不会考虑对手选择合作的条件下自己不同行动收益的效用之差, 所以此时${{u}_{c}}=0$, 那么在这种情况下, 表征决策者收益的哈密顿矩阵便修正为:
接下来, 我们便需要解决2.1中效用函数过度简化的问题, 即如何定义一个能够有效反映决策者收益之差的效用函数。我们选择使用预期理论中的价值函数, 并对其做适当的归一处理, 使其取值在-1与1之间, 以满足量子决策模型对于效用函数取值范围的要求:
其中${{D}_{D}}$表示当决策者已知对手背叛时, 选择背叛行动所获收益${{\pi }_{a}}$与选择合作所获收益${{\pi }_{b}}$的价值之差, 采用一种类似于逻辑回归的双曲正切函数对${{D}_{D}}$进行归一化处理。a为决策者在自身收益维度上的风险规避指数(risk-aversion parameter), 其值介于0到1之间。
其次, 当已知对手策略为合作时, 决策者也是基于“自己收益维度”做出决策的。此时哈密顿矩阵中${{u}_{c}}$表示决策者在知道对手背叛的条件下, 做出不同行动(背叛或合作)所获自身收益的效用之差。与上一种情况类似, 这种情况下决策者不会考虑对手选择背叛条件下自己不同行动收益的效用之差, 故而${{u}_{d}}=0$。此时, 哈密顿矩阵修正为:
其中,${{D}_{C}}$表示当决策者已知对手合作时, 选择背叛行动所获收益${{x}_{CD}}$与选择合作所获收益${{x}_{CC}}$的价值之差。
3.2.2 不确定条件下哈密顿矩阵的修正
当对手策略未知时, 决策者会将“他人收益维度”列入自己的决策标准之内。此时, 决策者决策时除了会参考自己的收益维度, 也会考虑他人的收益维度。此时的哈密顿矩阵便可以通过两个分别代表自身收益和他人收益的哈密顿矩阵叠加而成。
其中, 代表决策者自身收益的哈密顿矩阵可表示为:
而代表他人收益的哈密顿矩阵可表示为:
$\begin{matrix} & H_{0}^{2}=\left[ \begin{matrix} {{{{H}'}}_{D}} & 0 \\ 0 & {{{{H}'}}_{C}} \\\end{matrix} \right],{{{{H}'}}_{D}}=\frac{1}{\sqrt{1+{{{{u}'}}_{d}}^{2}}}\left[ \begin{matrix} {{{{u}'}}_{d}} & 1 \\ 1 & -{{{{u}'}}_{d}} \\\end{matrix} \right] \\ & {{{{H}'}}_{C}}=\frac{1}{\sqrt{1+{{{{u}'}}_{c}}^{2}}}\left[ \begin{matrix} {{{{u}'}}_{c}} & 1 \\ 1 & -{{{{u}'}}_{c}} \\\end{matrix} \right] \\ \end{matrix}$
其中$u'_{d}$与$u'_{c}$是他人维度上的效用函数, 分别表示当他人选择背叛/合作时, 决策者选择背叛时他人所获收益价值与决策者选择合作时他人所获收益价值之差的效用函数:
其中${{{D}'}_{D}}$表示当对手背叛时, 决策者选择背叛行动他人所获收益${{\pi }_{a}}$与决策者选择合作时他人所获收益${{\pi }_{c}}$的预期价值之差;${{{D}'}_{C}}$表示当对手合作时, 决策者选择背叛行动他人所获收益${{\pi }_{b}}$与决策者选择合作时他人所获收益${{\pi }_{d}}$的预期价值之差, 此时b为决策者在他人收益维度上的风险规避指数(risk- aversion parameter), 而相比于他人的收益, 决策者更加重视自身的收益, 即决策者在自身收益维度上效用函数的曲率(utility curvature)应小于在他人维度上的效用函数的曲率(Li & Taplin, 2002; Li, Taplin, & Zhang, 2007; 李纾, 2016), 由效用函数的曲率差异可知0 < b < a <1。那么, 在不确定条件下, 表征收益的哈密顿矩阵便更改为${{{H}'}_{0}}=H_{0}^{1}+H_{0}^{2}$。
3.3 齐当别思想下的量子决策模型对囚徒困境中分离效应的解释
分别将修正后的哈密顿矩阵${{{H}'}_{1}},{{{H}'}_{2}}$和${{{H}'}_{0}}$以及表征认知失调的哈密顿矩阵HB代入薛定谔方程, 可分别得出决策者在已知对手策略为背叛、已知对手策略为合作以及未知对手策略这三种条件下选择背叛的概率, 分别如下所示:
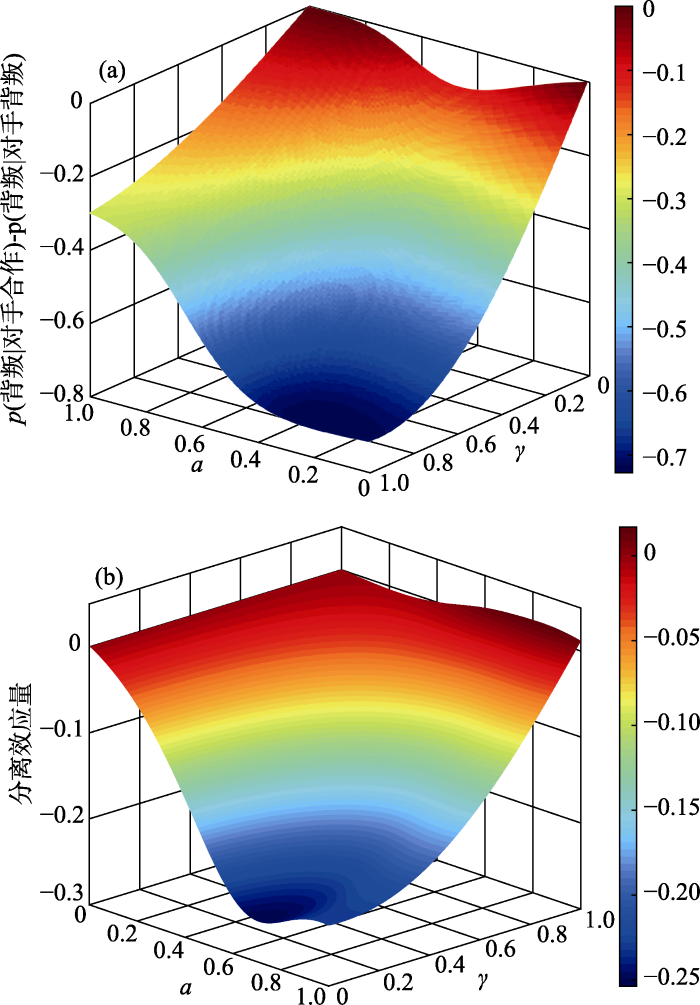
$M=\left[ \begin{matrix}{{M}_{1}} & 0 \\0 & {{M}_{2}} \\\end{matrix} \right]$, 其中${{M}_{1}}={{M}_{2}}=\left[ \begin{matrix}1 & 0 \\0 & 0 \\\end{matrix} \right]$, M的作用是将$\psi (t)$中的第一第三元素${{\psi }_{DD}}$和${{\psi }_{CD}}$选取出来。将Shafir和Tversky (1992)研究中的收益矩阵代入, 模型便构建完毕。接下来, 我们需要验证这种齐当别思想下的量子决策模型是否克服了之前量子决策模型中存在的困难。首先, 做出p(背叛│对手合作) - p(背叛│对手背叛)与参数a与g之间关系的3D着色表面图(图2(a)), 可以看出, 此时p(背叛│对手合作)总是小于p(背叛│对手背叛), 这样便解决了原量子决策模型中的第一个困难。接下来, 做出分离效应量与参数a与g之间的3D着色表面图(图2(b)), 从中可以看出, 当b = a/4时, 虽然模型可解释的最大分离效应量也为0.25, 但是其分布较为连续, 从而提升了模型对大分离效应量实验结果的拟合精度。特别地, 固定b = a/4, 使用最小绝对误差法进行拟合, 当a和γ分别取值为0.73与0.13时, 便可得出与Shafir和Tversky (1992)研究结果基本相同的拟合数值(如表2所示)。使用同样的拟合方法, 本文进一步对比分析了本研究所提出的量子决策模型和Pothos和Busemeyer (2009)提出的量子决策模型对于一些分离效应研究结果的拟合性能。如表2所示, 可以看出, 当模型的自由参数的数量相同时, 先前的量子决策模型对于分离效应量较大的研究结果(Shafir & Tversky, 1992; Busemeyer et al., 2006)的拟合效果较差, 而本研究所提出的量子决策模型则展现了优异的拟合效果。
图2
图2
本研究所提出的量子决策模型中p(背叛│对手合作) - p(背叛│对手背叛)以及分离效应量与a和g之间关系的3D着色表面图(其中模型参数b=a/4, t=3π/8)
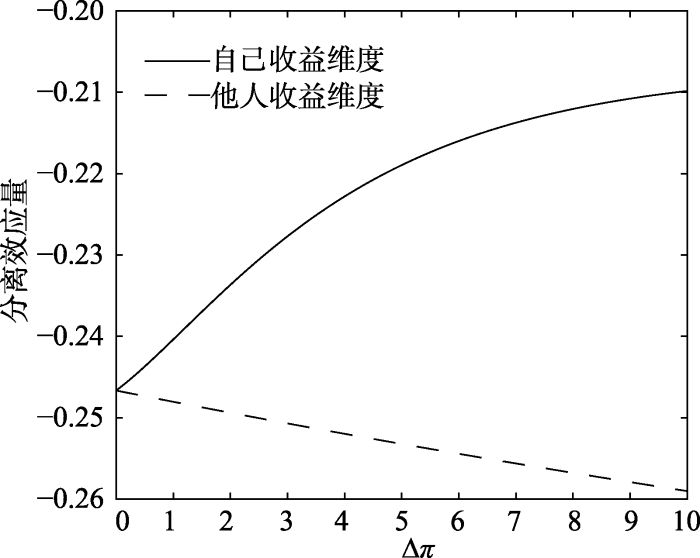
接下来, 便是验证这一模型能否解决原模型的第三个困难, 即能否正确地表示收益之差的效用与分离效应量之间的关系。按照相关研究的结论, 自己收益差距的增大, 会阻碍分离效应的发生, 即增大分离效应量的数值; 而他人收益差距的增大, 则会促进分离效应的发生, 即降低分离效应量的数值(Li & Taplin, 2002; Li, Taplin, & Zhang, 2007; 李纾, 2016)。因此, 根据定义, 增大自己的收益差距可看作增大式(6)中的${{\pi }_{a}}$与式(8)中的${{\pi }_{c}}$值; 而增大他人的收益差距可看作增大式(11)中的${{\pi }_{c}}$与式(12)中的${{\pi }_{d}}$值, 那么, 做出自己与他人收益增大量1( 即${{\pi }_{i}}\to {{\pi }_{i}}+\Delta \pi $自己收益维度下$i=\{a,c\}$; 他人收益维度下$i=\{c,d\}$。)$\Delta \pi $与分离效应量之间的关系, 如图3所示。从中可以看出, 当自己收益差距增大时, 分离效应量的数值变大, 分离效应减小; 而当他人的收益差距增大时, 分离效应量的数值变小, 分离效应增大, 这便说明本研究所提出的量子决策模型能够有效反映收益差距与分离效应之间的关系, 从而解决了原模型中的第三个困难。
图3
图3
本研究所提出的量子决策模型中收益增加量Δπ与分离效应量之间的关系(模型其余参数为拟合Shafir和Tversky (1992)研究所得参数)
4 讨论
4.1 启发式与计算式的融合
自从Herbert Simon提出“有限理性”的概念以来, 在此基础上形成的启发式(Heuristic)决策模型已经在决策领域取得了许多重要的成就(Baron, 2007; Gigerenzer & Todd, 1999; Tversky & Kahneman, 1974)。大多数启发式决策模型, 例如齐当别模型, 以决策模型的三因素分类体系来看, 属于非补偿性和确定性的决策模型(Stevenson, Busemeyer, & Naylor, 1990)。由于存在非补偿性, 这类模型会对一些信息进行简化或剔除, 进而简化分析过程; 但由于该模型的确定性(Kubovy, Rapoport, & Tversky, 1971; 李纾, 2016), 使其无法精确描述决策者在不同条件下做出决定的概率。
量子决策模型, 属于计算式(Computational)或数学(Mathematical)决策模型, 从决策模型的分类体系标准来看, 属于具有随机性的决策模型。因为其具有随机性, 可以通过概率函数的形式表征决策结果, 所以这类模型可以定量描述分离效应(Busemeyer & Townsend, 1993; Payne & Bettman, 2004)。但是, 先前的量子决策模型, 过度简化了模型的构建过程, 并缺乏对实际决策过程中决策者策略的深入思考。因此, 在解释分离效应时存在困难。
本研究所提出的量子决策模型, 立足于四维量子决策模型, 借鉴了齐当别思想对模型进行了重构。可以称之为一种计算式与启发式相融合的决策模型。而这种齐当别思想下的量子决策模型, 解决了先前量子决策模型中所存在的困难, 同时也为今后决策模型的构建添加了新的可能性。
4.2 囚徒困境中决策者信念与行为的纠缠
本研究所提出的量子决策模型中, 依旧保留了原量子模型中表示信念与行动纠缠的哈密顿矩阵HB。那么, 是否可以忽略这一纠缠效应, 进而完全按照齐当别思想来构建量子决策模型呢?本研究的结果表明, 当分离效应量较小时(如Li & Taplan (2002)的研究结果), 模型的最佳拟合参数中γ=0, 说明此时HB是可以去除的; 但当分离效应量较大时, 若去除HB, 则会使拟合误差大幅提升, 如对Shafir和Tversky (1992)的实验结果进行拟合时, 绝对误差便会从原先的0.04上升至0.09, 增大了两倍, 可见此时去除HB是不合适的。综上所述, 信念与行为的纠缠对于解释分离效应量较大的研究是不可或缺的。
5 结论与展望
本文提出了一种结合齐当别思想的量子决策模型, 研究表明这一模型解决了先前量子决策模型中存在的困难。当然, 正如量子决策模型的奠基者Jerome R. Busemeyer教授所指出的, 类似量子决策模型这样的数学决策模型, 就像刚刚进入决策之城的小孩子一样(Busemeyer & Johnson, 2008), 需要不断地成长才能获得属于自己的一席之地。因此, 作为这些“小孩子”中的一员, 本研究所提出的这种量子决策模型, 也有值得进一步探讨与发展之处, 主要总结为以下几点:
(1) 模型的扩展应用。本文提出的这种量子模型, 未来可以尝试解释诸如两阶段赌博任务中的分离效应, 以及分类-决策(Categorization-decision)实验中的干涉效应(Busemeyer et al., 2009; Townsend, Silva, Spencer-Smith, & Wenger, 2000; Wang & Busemeyer, 2016)等违背经典决策模型的问题。
(2) 模型的动态化探究。在量子决策模型中, 由于薛定谔方程以及其解中存在时间参数t, 因此量子模型又是一种动态的(Dynamical)模型(Busemeyer, Wang, & Townsend, 2006)。但是, 目前大多数相关研究中, 为了简化问题探讨, 往往将时间t设为固定值, 而在实际问题中, 决策时间的不同会对决策者的最终决策产生影响, 而对于量子决策模型来说也是如此, 因此, 探究一种具有“动态化”的量子决策模型也具有重要的理论和现实意义。
(3) 更加“真实”的量子决策模型。包括本研究在内的大多数动态量子决策模型, 都是“理想的”模型。例如, 模型中决策者的信念行为状态(包括基态以及叠加态), 是一种“纯净的”、“理想的”量子态(纯态), 这就意味着决策者(被试)间的差异可以忽略, 模型可以通过平均行为倾向来描述被试群体行为特点; 模型中的测量是“完美的”, 即在测量时(或要求被试报告结果时)所测得的结果能够完全表示决策者所处的信念行为状态(Yearsley, 2017)。但是在现实中, 由于受到各种条件的影响(噪音), 决策过程往往不会如此理想化。在未来的研究中, 通过在模型中构建适当的噪音, 不仅可增强模型的真实性, 而且可以据此来判别在一定的情况下是否真的存在分离效应抑或仅仅是实验中存在的“噪音”。
(4) 启发式决策模型与计算式决策模型的融合。长期以来, 计算式的决策模型(如决策场模型与马尔科夫决策模型)由于其较为复杂的数学结构, 往往不能为大多数研究者所理解; 而计算式决策模型的研究者, 在其构建模型的过程中, 往往将重心放在数学结构上, 从而忽视了与其相关的启发式决策模型。通过本研究的结果, 可以看出, 启发式决策模型与计算式决策模型能够很好地融合, 通过启发式的思想对计算式的模型进行改进, 不仅能够解决计算式模型中存在的一些困难, 而且能使启发式的思想以较为客观的数学形式展现出来, 让其具有量化解释问题的能力。因此, 启发式决策模型与计算式决策模型的融合, 具有重要的理论意义与广阔的发展前景。
致谢:
作者感谢两位匿名审稿专家对本文提出的严谨而富有建设性的意见。
参考文献
A comparison between two models of bounded rationality: Equate-to-differentiate and priority heuristic approaches
有限理性的"占优启发式"和"齐当别"决策模型的作为——当Allais悖论杠杆撬动了期望效用理论
Preferences and beliefs in a sequential social dilemma: A within-subjects analysis
DOI:10.1016/j.geb.2014.05.005 URL [本文引用: 1]
A quantum probability perspective on borderline vagueness
Quantum cognition: A new theoretical approach to psychology
DOI:10.1016/j.tics.2015.05.001 URL [本文引用: 1]
Quantum models of cognition and decision
Micro-process models of decision making
A quantum information processing explanation of disjunction effects
Decision field theory: A dynamic-cognitive approach to decision making in an uncertain environment
DOI:10.1037/0033-295X.100.3.432 URL [本文引用: 1]
What is quantum cognition, and how is it applied to psychology?
DOI:10.1177/0963721414568663 URL [本文引用: 1]
Applying quantum principles to psychology
Empirical comparison of markov and quantum models of decision making
DOI:10.1016/j.jmp.2009.03.002 URL [本文引用: 3]
Quantum models of cognition and decision
Quantum dynamics of human decision-making
DOI:10.1016/j.jmp.2006.01.003 URL
The disjunction effect and reason- based choice in games
DOI:10.1006/obhd.1999.2846 URL [本文引用: 1]
A quantum-like model for complementarity of preferences and beliefs in dilemma games
DOI:10.1016/j.jmp.2016.09.004 URL [本文引用: 1]
Simple heuristics that make us smart
Prospect theory: An analysis of decision under risk
Deterministic vs probabilistic strategies in detection
Choice reversals across certainty, uncertainty and risk: The equate-to-differentiate interpretation
确定、不确定及风险状态下选择反转:“齐当别”选择方式的解释
Bounded or unbounded rationality? The implication of equate-to-differentiate theory in economic behavior
无限理性还是有限理性?——齐当别抉择模型在经济行为中的应用
Examining whether there is a disjunction effect in prisoner's dilemma games
The equate-to- differentiate’s way of seeing the prisoner’s dilemma
DOI:10.1016/j.ins.2006.07.018 URL
Walking with the scarecrow: The information-processing approach to decision research
Models of decision making under risk and uncertainty
A quantum probability explanation for violations of ‘rational’decision theory
Thinking through uncertainty: Nonconsequential reasoning and choice
DOI:10.1016/0010-0285(92)90015-T URL [本文引用: 10]
Exploring the relations between categorization and decision making with regard to realistic face stimuli
Judgment under uncertainty: Heuristics and biases
DOI:10.1126/science.185.4157.1124 URL [本文引用: 1]
The framing of decisions and the psychology of choice
DOI:10.1126/science.7455683 URL [本文引用: 2]
The disjunction effect in choice under uncertainty
DOI:10.1111/j.1467-9280.1992.tb00678.x URL [本文引用: 3]
Interference effects of categorization on decision making
DOI:10.1016/j.cognition.2016.01.019 URL [本文引用: 3]
The disjunction effect in decision making
行为决策中出现的分离效应
Quantum models for decision making
一种新决策模型——量子决策模型
Advanced tools and concepts for quantum cognition: A tutorial