1 引言
决策对人类的生存和日常生活至关重要。虽然很多决策看似很小, 但累积效应却很大(Stewart, Hermens & Matthews, 2016), 如投资养老基金、自主创业等。近几十年, 决策受到行为经济学、心理学和社会学等领域的广泛研究, 取得了颇具价值的理论成果, 但人们究竟是如何进行决策的仍然是一个挑战性的问题。眼脑假设(Eye-mind hypothesis)认为, 眼睛注视的内容与大脑正在处理的内容没有明显的时间差(Just & Carpenter, 1980)。随着眼动技术(Eye movements)的发展, 决策过程的研究变得更加可行, 决策过程的研究随之也成为心理学和行为经济学的重点研究领域。眼动技术成为研究需要实时视觉感知的复杂决策过程的重要研究工具(Zhou et al., 2016)。
眼动技术是用于研究和分析眼球运动的技术, 眼球运动是指眼球从一个注视点移动到另一注视点的快速弹道运动。眼动技术包含时间和空间两个维度的指标, 具体而言, 在时间维度上包括注视时间、凝视时间、回视时间和总注视时间等, 在空间维度上包括眼跳距离、注视位置、注视次数、跳读率、再注视比率和回视次数等。我国学者闫国利等人(2013)曾对阅读中常见眼动指标进行了详细的综述, 对眼动技术在阅读和其他领域中的应用和推广具有重要意义。在决策研究领域中, 已有研究也常从时间和空间两个维度对决策过程的眼动信息进行分析(Stewart, Hermens, & Matthews, 2016; 魏子晗, 李兴珊, 2015; 王福兴, 侯秀娟, 段朝辉, 刘华山, 李卉, 2016), 以期揭示决策的认知过程。但在一定程度上忽视了决策中认知过程的时序性和整体性(Day, 2010; Glöckner & Herbold, 2011; Su et al., 2013; Sun, Rao, Zhou, & Li, 2014), 导致决策过程中诸多颇具价值的信息丢失, 阻碍了研究者更加精确、完整地揭示决策的认知过程。
近年来, 随着眼动数据分析技术的进一步发展, 研究者们开始探讨眼动指标在时间和空间两个维度相结合的眼动轨迹研究。眼动轨迹分析理论最早由Noton和Stark提出, 用来解释眼动模式的代表性本质(Noton & Stark, 1971)。该理论假设眼动轨迹是一个由内部化的认知模型驱动的眼动过程, 以自上而下的加工方式运行, 并在多次曝光时保持稳定。眼动轨迹通常反映视觉刺激在大脑中被处理的顺序。Noton和Stark及后继研究者提出了字符串序列(string)、概率模型(probabilistic models)和几何向量(geometrical vectors)等一系列定量的眼动轨迹分析方法, 如:Markov (1971)的马尔可夫概率模型(Markov chains), Noton和Stark (1971)的字符串编辑方法(Levenshtein距离法)以及Ponsoda, Scott和Findlay (1995)的包含眼跳方向的几何向量测量法。在已有的眼动轨迹分析方法中, 眼动轨迹匹配法(Scanmatch)是唯一同时考虑视觉元素的时空位置和注视持续时间的方法。该方法由Cristino, Mathôt, Theeuwes和Gilchrist (2010)提出, 是一种基于生物信息学中用于比较DNA序列的Needleman Wunsch (NLW)算法。近年来, 国内外研究者尝试着将眼动轨迹匹配法运用到决策等认知过程的研究中, 验证了眼动轨迹匹配法的精确性和有效性(Zhou et al., 2016; Madsen, Larson, Loschky, & Rebello, 2012)。但总体而言, 国内外研究者对该方法的研究和使用仍然较少, 国内决策领域的研究中仅有中科院李纾课题组报告了关于眼动轨迹匹配法的研究成果。该方法尚未得到广泛使用的原因可能是国内研究者对该方法的计算过程、特点和内在的心理学意义不够了解。鉴于此, 本文将在已有研究的基础上, 对眼动轨迹匹配法进行详细的介绍, 对其在决策领域中的研究进展进行全面归纳和评述, 并对未来的研究方向和应用范围进行展望。
2 眼动轨迹匹配法
眼动轨迹匹配法是Cristino等人(2010)在字符串编辑方法的基础上提出的, 主要通过注视数据的预处理、兴趣区划分和编码、形成眼动轨迹字符串、计算相似性得分四个步骤来对两个眼动轨迹的相似性进行比较, 以相似性得分的大小来衡量认知过程的异同。
第一步, 注视数据的预处理。眼动轨迹匹配法的第一步是对参与者的所有眼动数据进行预处理, 将兴趣区(Region of Interest, ROI)之外和注视时间小于50 ms的眼动数据移除(Nuthmann & Kliegl, 2009)。
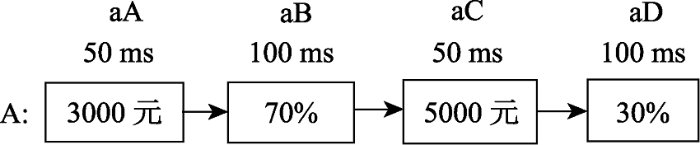
第二步, 兴趣区划分和编码。为了能够将眼动轨迹进行编码, 需根据研究目的将视觉场景划分为一系列不重叠的ROI, 为每个ROI都设置一个唯一的字符, 考虑到ROI的数量可能会超过26个(英文字母表的长度), 在眼动轨迹匹配法中常使用双字符编码, 即小写字母+大写字母(如图1中aA、aB、aC、aD) (Cristino et al., 2010)。
图1
第三步, 形成眼动轨迹字符串。为了能将ROI的单次注视持续时间编码到字符串中, 研究者需要根据研究目的设置基础注视时间(常用50 ms), 按照单次注视持续时间与基础注视时间的比例重复编码该ROI对应的字符进入字符串, 全部字符按照时间顺序排列就形成了眼动轨迹的字符串序列。如图1中的眼动轨迹可以编码为:aAaBaBaCaDaD。
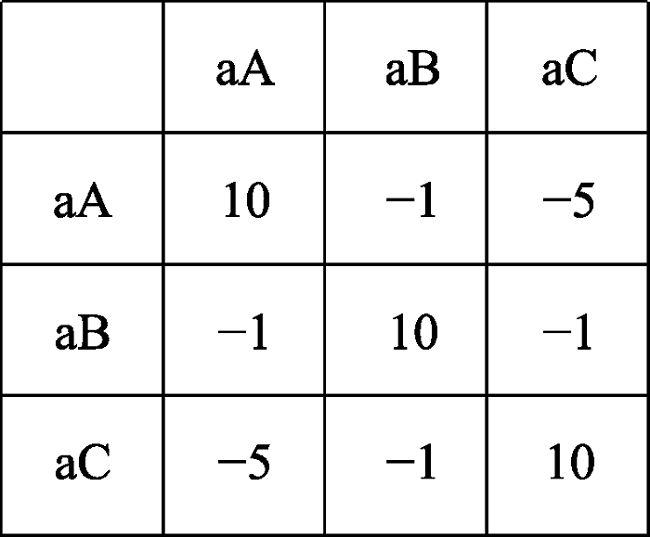
第四步, 计算相似性得分。Cristino等人(2010)使用广泛应用于生物信息学领域的Needleman Wunsch (NLW)算法来计算两个眼动轨迹间的最大相似性得分。首先需要设置一个替换矩阵, 为该矩阵的每一个对齐设置对齐分数(如图2)。为了使两个序列尽可能地对齐, 获得两个序列间的最大相似性得分, 研究者被允许在序列的任意位置加入间隙(gaps, 两个字符之间的空格), 并可以进行字符与间隙之间的对齐, 此时的对齐分数也称为间隙惩罚。两个眼动轨迹间的相似性得分即为整个序列的总对齐分数。不过, 此时的总对齐分数不仅与两个眼动轨迹间的相似性有关, 也与字符串的长度有关, 长度越长, 总对齐分数越高。例如, 在同一参数设置的情况下, 包含20个字符的两个完全相同的眼动轨迹总对齐分数必然高于只包含5个字符的两个完全相同的眼动轨迹总对齐分数, 但事实上, 每种情况下的两个眼动轨迹都是完全相同的, 理论上相似性得分也应该相同。因此, 为了克服字符串长度对相似性得分的影响, Cristino等人(2010)提出相似性得分的标准化公式:$\frac{总对齐分数}{替换矩阵最大对齐分数最长字符串的字符数量}$
图2
图2
替换矩阵举例(资料来自Cristino et al., 2010)
通过使用标准化公式, 两个眼动轨迹间的最高相似性得分为1分, 相似性得分越接近1, 眼动轨迹越相似。
替换矩阵中的对齐分数和间隙惩罚是两个需要根据眼动轨迹以及ROI之间的关系进行设置的重要参数。ROI之间的关系越亲近, 对齐分数设置越高, 同一ROI之间的对齐分数最高。ROI之间的关系既可以基于空间位置, 也可以基于属性维度, 这为研究决策等认知过程带来了便利。另一个需要设置的参数是间隙惩罚分数。如果间隙惩罚过高会导致相似性得分的偏低, 具有一定相似度的两个眼动轨迹会被误认为没有相似性; 而间隙惩罚为零或过低会导致相似性得分的偏高, 相似度很小的两个眼动轨迹会被误认为具有较高的相似性。在图3中介绍了间隙惩罚的两种分数设置以及最优解, 研究者可根据其研究目的对这些参数进行个性化设置。虽然, 对齐分数和间隙惩罚分数设置的主观性会导致眼动轨迹相似性得分的绝对大小存在波动(Eraslan, Yesilada, & Harper, 2015)。但在同一参数设置条件下, 眼动轨迹间的相似性得分的相对大小是稳定的, 具有可比性。
图3
图3
间隙惩罚和相似性得分计算举例(资料改自Cristino et al., 2010)
Cristino等人编制了适用于Matlab软件的应用程序——眼动轨迹匹配工具箱(Scanmatch toolbox), 可对眼动轨迹的相似性得分进行快速匹配分析。研究者可通过
3 眼动轨迹匹配法在决策领域的应用
眼动轨迹被认为是由个体内化的认知模型所驱动, 以一种自上而下的认知加工方式形成, 反映大脑对视觉刺激的加工顺序和整体动态的眼动过程(Gbadamosi & Zangemeister, 2001; Noton & Stark, 1971; Underwood, Humphrey, & Foulsham, 2008)。这种自上而下的加工方式决定了人们在采用相同策略进行决策时的眼动轨迹是相对稳定的, 而采用不同策略进行决策时会产生差异较大的眼动轨迹。对决策任务间眼动轨迹相似性得分的计算和比较, 可以揭示决策过程中所遵循的决策理论模型, 以及决策的相关影响因素。
3.1 决策相关理论的研究
行为决策领域对风险决策的相关理论一直存在争论, 主要涉及两种理论模型之争:一是源于无限理性的折扣模型, 如期望价值理论(Pascal, 1660)及以预期理论(prospect theory) (Kahneman & Tversky, 1979)为主的概率折扣(probability discounting)理论, 即人们在做决策时是基于选项的、补偿性策略, 将选项中的概率维度和结果维度进行整合并比较效用的大小, 据此选择最优结果。二是基于有限理性的非折扣模型, 如占优启发式模型(priority heuristic) (Brandstätter, Gigerenzer, & Hertwig, 2006)和齐当别模型(equate-to- differentiate model) (Li, 2004)等, 即人们在做决策时是基于维度的、非补偿性策略, 个体只根据选项中的个别维度进行比较, 据此做出决策。为了解决这一理论争议, 近年来, 研究者开始逐渐探索使用眼动轨迹匹配法来验证决策的相关理论模型。Zhou (2014)最早采用与眼动轨迹匹配法类似的算法对被试在决策过程中所使用的策略(补偿性或非补偿性)进行了研究, 不过该实验采用的不是眼动技术, 而是鼠标跟踪技术(除鼠标移动到的位置, 其他信息均被掩盖)来获取决策的过程序列。参与者被要求陆续使用补偿性和非补偿性策略在三套假设的公寓中做出选择, 结果发现, 与非补偿性策略相比, 被试使用补偿性策略所产生的决策过程序列与被试自由决策时的序列具有更高的相似性。该研究虽然不是使用眼动技术, 但采用了眼动轨迹匹配法中相似性得分的算法, 这为眼动轨迹匹配法用于决策理论的研究提供了算法上的支持。
随后, 研究者开始将眼动轨迹匹配法正式应用到决策理论的研究中, 取得了一系列颇具价值的成果。Zhou等人(2016)首次使用眼动轨迹匹配法来探讨决策者在风险决策中所采用的决策策略。该研究共分析了三组实验数据, 每个实验分基线条件和实验条件, 基线条件包括比例决策任务、结果匹配呈现风险决策任务和结果多重应用风险决策任务, 实验条件包括概率决策任务、结果交叉呈现风险决策任务和结果单一应用风险决策任务。采用眼动轨迹匹配法对各实验中的条件内和条件间的眼动轨迹相似性得分进行计算, 通过比较条件内与条件间的相似性得分大小来判断两种条件下决策过程的异同, 从而验证风险决策中所采用的决策策略。其所遵循的逻辑是, 当风险决策的结果以匹配或交叉方式呈现时, 如果条件内和条件间的相似性得分没有显著差异, 那么风险决策不受结果呈现方式的影响, 风险决策是基于选项的补偿策略, 反之, 则是基于维度的非补偿策略。比例任务和结果多重应用风险决策任务已被证实是基于补偿性策略的(张阳阳, 饶俪琳, 梁竹苑, 周媛, 李纾, 2014; Sun et al, 2014)。研究结果发现, 三个实验中条件内的相似性得分均显著高于条件间的相似性得分。这表明各实验中基线条件和实验条件的眼动轨迹存在较大差异, 从而证明了两种条件下决策的认知过程是不同的, 支持了风险决策(结果单一应用)过程是采用基于维度的、非补偿策略。此外, 研究者还对三个实验中各条件下的典型试次(与其他所有试次间的平均相似性得分最高的试次)的眼动轨迹进行了观察, 发现不同条件下典型试次的眼动轨迹模式也存在较大差异, 进一步验证了上述的研究结论。这也与已有关于决策理论的相关研究结果相一致(Su et al., 2013; Sun et al., 2014; Mathôt, Cristino, Gilchrist, & Theeuwes, 2012)。由此可见, 眼动轨迹匹配法对于研究决策的相关理论模型是可靠且有效的新方法。
周蕾等人(2018)在其随后的研究中进一步利用眼动轨迹匹配法对风险决策和跨期决策的认知过程进行了比较。结果发现, 无论是否包含确定选项/即刻选项, 风险决策和跨期决策任务间的眼动轨迹相似性分数均显著低于任务内的眼动轨迹相似性得分。典型试次的进一步观察发现, 风险决策中存在较多的基于维度的眼跳; 而跨期决策中并未发现明显占优势的基于维度或选项的眼动过程。由此可见, 风险决策和跨期决策的决策过程可能基于不同的决策策略, 决策者在跨期决策中的决策策略更加复杂。这一研究创新的采用眼动轨迹匹配法为风险决策和跨期决策之间认知过程的比较提供了新证据, 而且也是对跨期决策理论的一种新探索。
综上, 眼动轨迹匹配法在决策相关理论的研究中具有良好的适用性。未来的研究还可以采用眼动轨迹匹配法对跨期决策、模糊决策、社会决策等各类决策的认知过程进行探讨, 并进一步对风险决策中的启发式、齐当别等非补偿性策略进行细致的研究。例如, 在“迫选规则体验法”范式中, 可以要求被试分别进行遵循加权求和的迫选任务、遵循启发式的迫选任务和自由决策任务, 采用眼动轨迹匹配法计算并比较两种迫选任务与自由决策任务间的眼动轨迹相似性得分的差异。眼动轨迹相似性得分更高, 自由决策更有可能遵循该迫选任务中所采用的决策策略。此外, 另一个验证决策理论的重要方法是, 通过眼动轨迹匹配法计算出各任务中的典型试次, 通过直观地观察典型试次的眼动轨迹模式, 来判断所采用的决策策略。例如, 占优启发式的主要决策特点是, 决策者对最小结果的注视次数更多。通过将典型试次的眼动轨迹模式与占优启发式的这一特点进行比较, 就可以直观地判断被试是否采用了该策略。
3.2 决策相关影响因素的研究
自Cristino等人(2010)提出眼动轨迹匹配法之后, 后继的研究者也开始使用眼动轨迹匹配法对决策的影响因素进行了探索性研究。Zhou (2014)使用眼动轨迹匹配法探讨了决策情境中的时间压力对决策过程的影响。被试被要求陆续在决策时间为6 s、12 s、18 s、24 s、30 s和36 s六种情境下对将要观看的电影进行决策, 以36 s作为基线条件, 结果发现决策时间越接近, 眼动轨迹的序列相似度越高; 被试在12 s和6 s两个条件下的眼动轨迹差异最大。这表明当面临超负荷的时间压力时决策者会过度紧张, 以至于遗忘了自己的正常决策策略。类似的, Dewhurst等人(2012)也发现了任务难度对决策策略和眼动轨迹的影响。他们发现随着任务难度的增加, 眼动轨迹相似性得分逐渐降低, 产生更多差异性的决策策略和眼动轨迹。除了外在的影响因素, 眼动轨迹匹配法也被用于解释个体内在因素对行为决策的影响。Khedher, Jraidi和Frasson (2018)采用眼动轨迹匹配法对医学生的医疗诊断决策进行了研究, 他们首先构建了诊断健忘症的正确推理过程, 随后与医学生实际推理过程中的眼动轨迹进行比较。结果发现, 学生推理能力越强, 相似性得分越高, 越能够做出正确的诊断决策。不过, 该研究认为推理过程中注视ROI的顺序是主要因素, 因此在计算眼动轨迹相似性得分时未考虑ROI的单次注视时间。
最近, Król和Król (2019)在一项金融投资反馈任务中, 探索性地使用了与眼动轨迹匹配法类似的字符串编辑法应用于提高经济决策的质量。他们将被试做自由决策时的眼动轨迹与正确决策时的眼动轨迹进行相似性比较, 并向被试反馈相似性情况, 结果发现通过反馈学习, 决策者逐渐学会了正确决策的眼动轨迹, 从而做出了正确的决策。不过, 该研究中的字符串编辑法仅考虑了眼动数据中的顺序信息, 未考虑注视时间。可以推测, 如果向决策者反馈采用眼动轨迹匹配法计算出的相似性得分, 或者直接提供正确决策的典型试次的眼动轨迹, 可以使决策者更加完整地了解正确决策的注意过程和加工深度, 掌握做出正确决策的有效路径和关键环节, 更有利于决策者做出正确决策。不过, 这个研究的前提是研究者首先要能够获得正确决策的典型试次的眼动轨迹。因此, 这种提高决策质量的方法可能适用于一些具有固定步骤和流程的程序化决策, 而不适用于那些具有多种创新思路的非程序化决策。因为这些决策可能没有指向正确决策结果的固定路径。另外, 这类方法可能更适用于一些新手, 为他们提供了通往正确决策的基本路径。而对于专家型选手可能并不需要按部就班的典型试次来指导。
总之, 眼动轨迹匹配法在决策领域地广泛运用将使研究者对决策“知其然, 且知其所以然”, 对于揭示框架效应、心理距离、情绪等相关变量影响决策过程的认知机制具有较高的应用前景。值得注意的是, 眼动轨迹匹配法是计算两个眼动轨迹之间的相似性得分, 一般涉及同一因素的两个水平间地比较。因此, 在决策的影响因素研究中, 当一个因素仅存在两个水平时, 可直接进行相似性得分计算, 分数越接近1, 决策过程越相似。而当因素水平超过两个时, 研究者可将其中一个水平(如情绪因素中的中性情绪)设置为基线条件, 通过计算基线条件与其他条件(如负性情绪和正性情绪)的眼动轨迹相似性得分, 以探究该因素的各个水平对决策过程的不同影响。
4 小结与展望
综上所述, 眼动轨迹匹配法能够准确、有效地揭示人们在复杂决策过程中的注意过程和认知机制, 对完善决策的理论模型及其影响因素的探究具有重要意义。这可能得益于眼动轨迹匹配法具有以下三个鲜明的特色。
首先, 眼动轨迹匹配法最大的优势可能是其可以计算出各任务下决策的典型试次, 通过直观地观察各任务中典型试次的眼动轨迹, 就可以掌握基于整体动态的决策过程。从整体动态的角度分析决策能够更具体、直观和全面地了解决策中的思维过程、决策者所采用的决策策略以及发现决策过程中的关键分歧, 这对于揭示不同决策策略的认知过程具有重要意义。在已有关于眼动与决策的研究中, 研究者多采用局部的眼动数据, 缺少对整体的眼动轨迹进行分析。个别研究通过绘制多个眼动轨迹图(陈庆荣 等, 2012; Sperati, 2003)和眼动轨迹坐标(陈丽君, 郑雪, 2014)的方法来描述整体的认知过程, 但典型试次的眼动轨迹模式仅用一个轨迹就可以完整地描述决策的认知过程, 更具体、简便, 也更具代表性。
其次, 眼动轨迹匹配法在评估两个注视序列的相似性时考虑了ROI的单次注视持续时间, 而其他定量的眼动轨迹分析方法都忽略了ROI的单次注视时间。事实上, 信息的注视时间与信息加工的深度和难易程度有显著的关系(Velichkovsky et al., 2002; Follet, Meur, & Baccino, 2011), 尤其是在需要对信息进行深度加工的决策等高级认知过程中。因此, 当研究者想要揭示决策中的认知过程时, 使用考虑注视持续时间的眼动轨迹匹配法最为合适。有研究对眼动轨迹匹配法的精确性进行了比较研究, 结果发现采用眼动轨迹匹配法和字符串编辑距离法所得的代表性眼动轨迹(representative scanpath) (与其他轨迹之间的总距离最小)之间的相关性为0.74。进一步将两种方法得出的最优代表性眼动轨迹和次优代表性眼动轨迹进行多维定标(multi-dimensional scaling, MDS)分析发现, 眼动轨迹匹配法所得的最优和次优代表性眼动轨迹间的相似度更高, 这表明眼动轨迹匹配法比字符串编辑距离法具有更高的精确度(Takeuchi & Matsuda, 2012)。
最后, 眼动轨迹匹配法的另一个优势是, 允许研究者根据研究需要对ROI基于认知、感知或任务的任何维度上进行相似性分类, 据此设置替换矩阵中ROI之间的对齐分数, 这对于决策领域的研究极为重要。因为, 在决策任务中ROI之间的逻辑关系常常不仅限于空间维度, 更有可能基于属性维度, 如:价值属性、概率属性、比例属性等。这些ROI可能在空间位置上离的很远, 但由于隶属于同一属性, 在设置替换矩阵参数时其对齐得分应该具有较高的赋值。例如, 在风险决策任务中, 研究者可以将空间距离较近的同一备选方案中的ROI之间的对齐分数设置为较高的分数(如5分), 也可以将空间距离较远但隶属于同一属性(概率或价值)的ROI间的对齐分数同样设置为5分, 而将空间距离远, 也不隶属于同一属性的ROI间的对齐分数设置为-5分。
虽然, 眼动轨迹匹配法是研究决策等认知过程的颇具价值的研究工具。但目前在决策领域应用眼动轨迹匹配法的研究仍然较少, 未来的研究者应进一步综合考虑该方法的优缺点, 通过实验设计扬长避短, 在以下几个方面开展更加深入的研究。
第一, 已有关于决策的相关理论模型虽然对决策结果有着相同的预测(Johnson et al., 2008), 但对决策过程的假设存在着巨大的差异, 甚至相互矛盾。正如上文所述, 预期理论(Kahneman & Tversky, 1979)能够很好地拟合风险决策的结果, 看起来是一个非常正确的理论(Glöckner & Herbold, 2011; Suter et al., 2016)。然而, 包括采用眼动轨迹匹配法在内的诸多研究都表明, 决策过程并非像预期理论所假设地进行加权求和的过程(Zhou et al., 2016; Zhou, Zhang, Li, & Liang, 2018)。除了风险决策外, 在跨期决策、模糊决策、社会决策等领域的理论模型中也存在诸多争论, 在采用现有研究方法仍然无法形成一致性结论的背景下, 眼动轨迹匹配法可能是进一步解决这些理论争议的重要方法。未来的研究可进一步加强眼动轨迹匹配法在各种决策理论模型中的验证性研究, 以期构建更加完善的决策理论模型。
第二, 决策是一个复杂的认知过程(Rogers, 2011), 它依赖于许多控制功能, 包括选择、抑制、工作记忆、情感、评估、反馈以及执行功能等。因此, 决策过程中的任何一个控制功能受到影响, 其决策行为都将随之发生变化。已有诸多研究发现心理距离、得失框架、个体特质等因素均会对个体决策产生影响, 研究者提出了解释水平理论、情绪维持假说等理论来解释这些变量对决策的影响(Trope & Liberman, 2000; Isen & Patrick, 1983)。不过, 这些理论大多缺乏决策过程数据的支持。也有研究者从认知神经科学的角度探索相关变量对决策过程中前额皮质、前扣带皮层等相关脑区活动情况的影响(Gleichgerrcht et al., 2010), 以揭示其认知神经机制。不过, 决策任务往往涉及的视觉信息较多且复杂, 而神经科学的方法无法对信息的获取进行精确的空间、时间和顺序地定位。在未来的研究中, 可以结合认知神经科学技术和眼动技术, 采用眼动轨迹匹配法将时间、空间及顺序信息与神经科学数据进行同步分析, 以进一步揭示决策的认知过程及其影响因素。
第三, 在实验设计和信效度检测方面, 眼动轨迹匹配法也具有较高的应用价值。在行为实验中, 被试由于各种原因, 经常会出现未按照实验要求完成决策任务, 对研究数据产生污染, 进而导致研究结果的失真。现有的研究方法很难精确地筛选出这些无效数据, 而利用眼动轨迹匹配法中的相似性得分和典型试次的眼动轨迹可以诊断出未按试验要求进行的无效决策。当被试采用一种不利的或错误的决策策略, 或是以疲劳或超认知负荷的状态进行决策时, 该方法能够有效的筛选出这些无效数据。在最近的一项研究中, Schoemann等人(2019)已探索性地采用眼动轨迹来检测被试是否按照规定策略进行了决策。由此可见, 未来的研究应进一步加强眼动轨迹匹配法在提高决策实验信效度中的应用, 确保数据的准确性和可靠性。
参考文献
中国象棋经验棋手与新手的知觉差异:来自眼动的证据
DOI:10.3724/SP.J.1041.2016.00457
URL
[本文引用: 1]

为探讨中国象棋领域内的专长效应及象棋专长的知觉编码优势, 研究采用中国象棋棋局为实验材料, 对比了经验棋手和新手在观看象棋棋局时视觉搜索、变化觉察和对棋盘的记忆。实验1呈现真实棋局和随机棋局, 要求被试观看5秒后复盘, 结果发现经验棋手的复盘正确率高于新手; 经验棋手注视棋盘的眼跳幅度和瞳孔直径更大; 经验棋手更多注视棋子间而不是棋子本身。实验2采用移动窗口范式控制了观看棋盘时视野大小, 结果发现经验棋手在副中央凹呈现时复盘正确率更高, 而新手不受视野大小的影响。实验3采用闪烁范式要求棋手觉察变化的棋子, 结果发现经验棋手的觉察速度和正确率都优于新手; 而且经验棋手在报告变化前就利用中央凹和副中央凹注视到了变化的棋子。结论认为:中国象棋与国际象棋类似, 也存在专长的知觉编码优势效应; 经验棋手不仅对棋盘记忆更好, 而且可以利用存贮的组块和长期练习经验选择性加工棋盘结构信息, 利用副中央凹提取信息, 具有更大的知觉广度。研究为象棋专家可以利用副中央凹加工棋盘及具有更强的知觉编码能力提供了直接的证据。
The priority heuristic: Making choices without trade-offs
DOI:10.1037/0033-295X.113.2.409
URL
PMID:16637767
[本文引用: 1]

Bernoulli's framework of expected utility serves as a model for various psychological processes, including motivation, moral sense, attitudes, and decision making. To account for evidence at variance with expected utility, the authors generalize the framework of fast and frugal heuristics from inferences to preferences. The priority heuristic predicts (a) the Allais paradox, (b) risk aversion for gains if probabilities are high, (c) risk seeking for gains if probabilities are low (e.g., lottery tickets), (d) risk aversion for losses if probabilities are low (e.g., buying insurance), (e) risk seeking for losses if probabilities are high, (f) the certainty effect, (g) the possibility effect, and (h) intransitivities. The authors test how accurately the heuristic predicts people's choices, compared with previously proposed heuristics and 3 modifications of expected utility theory: security-potential/aspiration theory, transfer-of-attention-exchange model, and cumulative prospect theory.
Scanmatch: A novel method for comparing fixation sequences
Examining the validity of the Needleman- Wunsch algorithm in identifying decision strategy with eye-movement data
Eye Tracking Scanpath Analysis Techniques on Web Pages: A Survey, Evaluation and Comparison
New insights into ambient and focal visual fixations using an automatic classification algorithm
Visual imagery in hemianopic patients
DOI:10.1162/089892901753165782 URL [本文引用: 1]
Decision-making cognition in neurodegenerative diseases
An eye-tracking study on information processing in risky decisions: Evidence for compensatory strategies based on automatic processes
DOI:10.1002/bdm.v24.1 URL [本文引用: 2]
The effect of positive feelings on risk taking: When the chips are down
Process models deserve process data: A comment on Brandstätter, Gigerenzer, and Hertwig 2008
A theory of reading: From eye fixations to comprehension
Prospect theory: An analysis of decision under risk
Local sequence alignment for scan path similarity assessment
Learning from peers’ eye movements in the absence of expert guidance: A proof of concept using laboratory stock trading, eye tracking, and machine learning
A behavioral choice model when computational ability matters
Extension of the limit theorems of probability theory to a sum of variables connected in a chain
In
A simple way to estimate similarity between pairs of eye movement sequences
Scanpaths in eye movements during pattern perception
An examination of binocular reading fixations based on sentence corpus data
A probability vector and transition matrix analysis of eye movements during visual search
The roles of dopamine and serotonin in decision making: Evidence from pharmacological experiments in humans
Forward inference in risky choice: Mapping gaze and decision processes
The inner working of dynamic visuo-spatial imagery as revealed by spontaneous eye movements
In J. Hyona, R. Radach, & H. Deubel (Eds.),
Eye movements in risky choice
Is making a risky choice based on a weighting and adding process? An eye-tracking investigation
Formulating an emergency plan based on expectation- maximization is one thing, but applying it to a single case is another
How affect shapes risky choice: Distorted probability weighting versus probability neglect
Temporal construal and time-dependent changes in preference
Knowledge-based patterns of remembering: Eye movement scanpaths reflect domain experience
Towards an express-diagnostics for level of processing and hazard perception
New paradigms for the old question: Challenging the expectation rule held by risky decision-making theories
A scanpath analysis of the risky decision-making process