

CN 11-1911/B


Acta Psychologica Sinica ›› 2020, Vol. 52 ›› Issue (9): 1132-1142.doi: 10.3724/SP.J.1041.2020.01132
• Reports of Empirical Studies • Previous Articles
ZHAN Peida1( ), JIAO Hong2, MAN Kaiwen3
), JIAO Hong2, MAN Kaiwen3
Received:2020-03-02
Published:2020-09-25
Online:2020-07-24
Contact:
ZHAN Peida
E-mail:pdzhan@gmail.com
Supported by:ZHAN Peida, JIAO Hong, MAN Kaiwen. (2020). The multidimensional log-normal response time model: An exploration of the multidimensionality of latent processing speed. Acta Psychologica Sinica, 52(9), 1132-1142.
| Items | θ1 | θ2 | θ3 |
|---|---|---|---|
| CM015Q02D | 1 | ||
| CM015Q03D | 1 | ||
| CM020Q01 | 1 | ||
| CM020Q02 | 1 | ||
| CM020Q03 | 1 | ||
| CM020Q04 | 1 | ||
| CM038Q03T | 1 | ||
| CM038Q05 | 1 | ||
| CM038Q06 | 1 |
Table 1 Q-matrix for PISA 2012 released computer-based mathematics items
| Items | θ1 | θ2 | θ3 |
|---|---|---|---|
| CM015Q02D | 1 | ||
| CM015Q03D | 1 | ||
| CM020Q01 | 1 | ||
| CM020Q02 | 1 | ||
| CM020Q03 | 1 | ||
| CM020Q04 | 1 | ||
| CM038Q03T | 1 | ||
| CM038Q05 | 1 | ||
| CM038Q06 | 1 |
| Model | χ2 | df | TLI | CFI | AIC | BIC | SRMR | RMSEA (90% CI) |
|---|---|---|---|---|---|---|---|---|
| 1-factor | 462.79** | 27 | 0.896 | 0.922 | 24592.15 | 24737.03 | 0.045 | 0.101 (0.093, 0.109) |
| 2-factor | 225.49** | 19 | 0.930 | 0.963 | 24370.85 | 24558.65 | 0.032 | 0.083 (0.073, 0.093) |
| 3-factor | 32.66** | 12 | 0.989 | 0.996 | 24192.02 | 24417.38 | 0.010 | 0.033 (0.020, 0.047) |
| 4-factor | 5.56 | 6 | 1.000 | 1.000 | 24176.92 | 24434.48 | 0.004 | 0.000 (0.000, 0.031) |
| 5-factor | 0.09 | 1 | 1.006 | 1.000 | 24181.44 | 24465.83 | 0.000 | 0.000 (0.000, 0.045) |
Table 2 Exploratory factor analysis model-data fit indexes for response times data
| Model | χ2 | df | TLI | CFI | AIC | BIC | SRMR | RMSEA (90% CI) |
|---|---|---|---|---|---|---|---|---|
| 1-factor | 462.79** | 27 | 0.896 | 0.922 | 24592.15 | 24737.03 | 0.045 | 0.101 (0.093, 0.109) |
| 2-factor | 225.49** | 19 | 0.930 | 0.963 | 24370.85 | 24558.65 | 0.032 | 0.083 (0.073, 0.093) |
| 3-factor | 32.66** | 12 | 0.989 | 0.996 | 24192.02 | 24417.38 | 0.010 | 0.033 (0.020, 0.047) |
| 4-factor | 5.56 | 6 | 1.000 | 1.000 | 24176.92 | 24434.48 | 0.004 | 0.000 (0.000, 0.031) |
| 5-factor | 0.09 | 1 | 1.006 | 1.000 | 24181.44 | 24465.83 | 0.000 | 0.000 (0.000, 0.045) |
| Item | Factor 1 | Factor 2 | Factor 3 |
|---|---|---|---|
| CM015Q02D | 0.695* | ||
| CM015Q03D | 0.609* | ||
| CM020Q01 | 0.565* | ||
| CM020Q02 | 0.801* | ||
| CM020Q03 | 0.642* | ||
| CM020Q04 | 0.943* | ||
| CM038Q03T | 0.502* | ||
| CM038Q05 | 0.985* | ||
| CM038Q06 | 0.621* |
Table 3 Rotated factor loading matrix for the 3-factor model for response times data
| Item | Factor 1 | Factor 2 | Factor 3 |
|---|---|---|---|
| CM015Q02D | 0.695* | ||
| CM015Q03D | 0.609* | ||
| CM020Q01 | 0.565* | ||
| CM020Q02 | 0.801* | ||
| CM020Q03 | 0.642* | ||
| CM020Q04 | 0.943* | ||
| CM038Q03T | 0.502* | ||
| CM038Q05 | 0.985* | ||
| CM038Q06 | 0.621* |
| Analysis Model | -2LL | DIC | WAIC | ppp |
|---|---|---|---|---|
| MLRTM | 19305 | 22505 | 22055 | 0.633 |
| ULRTM | 21310 | 22890 | 22770 | 0.597 |
Table 4 Indices for model fitting in the analysis of computer-based mathematical test data for PISA 2012 computer-based mathematics test
| Analysis Model | -2LL | DIC | WAIC | ppp |
|---|---|---|---|---|
| MLRTM | 19305 | 22505 | 22055 | 0.633 |
| ULRTM | 21310 | 22890 | 22770 | 0.597 |
| Στ | τ1 | τ2 | τ3 |
|---|---|---|---|
| τ1 | 0.301 (0.016) [0.270, 0.334] | 0.751 | 0.767 |
| τ2 | 0.185 (0.010) [0.167, 0.204] | 0.202 (0.010) [0.184, 0.220] | 0.855 |
| τ3 | 0.227 (0.012) [0.206, 0.250] | 0.208 (0.009) [0.190, 0.226] | 0.292 (0.013) [0.266, 0.317] |
Table 5 Estimates of variance-covariance matrix of multidimensional latent processing speed for PISA 2012 computer-based mathematics test
| Στ | τ1 | τ2 | τ3 |
|---|---|---|---|
| τ1 | 0.301 (0.016) [0.270, 0.334] | 0.751 | 0.767 |
| τ2 | 0.185 (0.010) [0.167, 0.204] | 0.202 (0.010) [0.184, 0.220] | 0.855 |
| τ3 | 0.227 (0.012) [0.206, 0.250] | 0.208 (0.009) [0.190, 0.226] | 0.292 (0.013) [0.266, 0.317] |
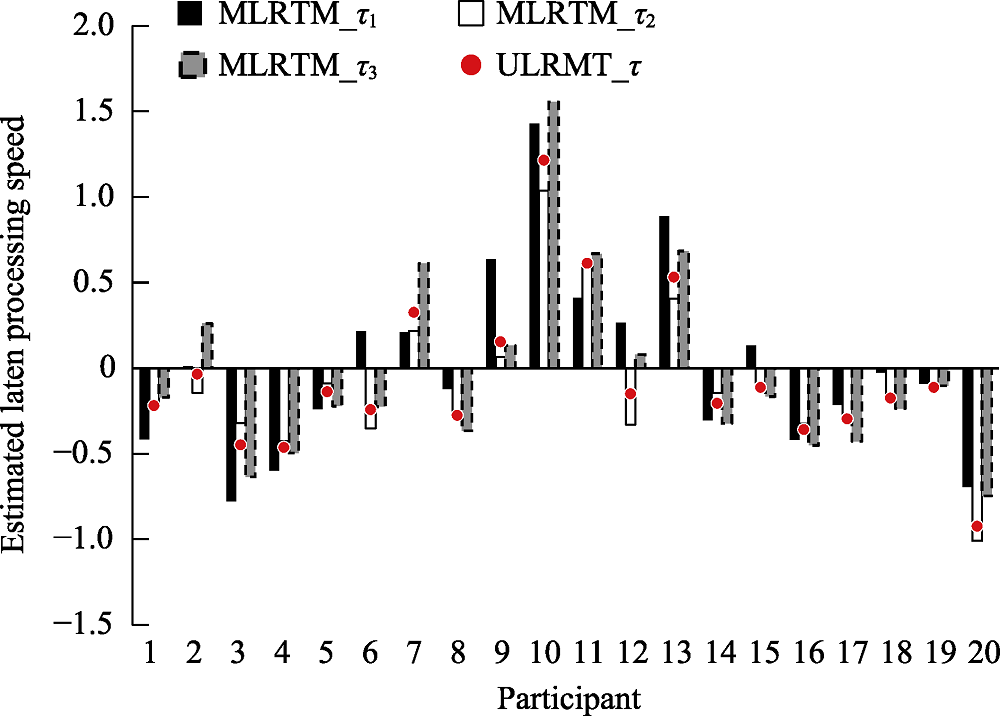
Figure 1. Estimates of latent processing speed for the first 20 participants in the PISA 2012 computer-based mathematics test Note. ULRTM = unidimensional log-normal response time model; MLRTM = multidimensional log-normal response time model; τ = latent processing speed.
| Item | ULRTM | MLRTM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ξ | ω | ξ | ω | |||||||||
| M | SE | 95% CI | M | SE | 95% CI | M | SE | 95% CI | M | SE | 95% CI | |
| 1 | 4.470 | 0.020 | [4.432, 4.508] | 1.617 | 0.031 | [1.558, 1.678] | 4.469 | 0.020 | [4.433, 4.510] | 1.845 | 0.045 | [1.760, 1.936] |
| 2 | 4.630 | 0.019 | [4.592, 4.667] | 1.697 | 0.032 | [1.635, 1.762] | 4.629 | 0.019 | [4.594, 4.668] | 1.976 | 0.051 | [1.874, 2.076] |
| 3 | 4.778 | 0.016 | [4.750, 4.811] | 2.423 | 0.050 | [2.327, 2.519] | 4.778 | 0.015 | [4.747, 4.807] | 2.505 | 0.055 | [2.397, 2.612] |
| 4 | 3.860 | 0.018 | [3.825, 3.895] | 1.866 | 0.036 | [1.793, 1.934] | 3.859 | 0.017 | [3.825, 3.894] | 1.915 | 0.038 | [1.841, 1.991] |
| 5 | 4.258 | 0.016 | [4.226, 4.291] | 2.186 | 0.044 | [2.104, 2.274] | 4.258 | 0.016 | [4.224, 4.287] | 2.202 | 0.047 | [2.112, 2.295] |
| 6 | 3.739 | 0.017 | [3.707, 3.774] | 2.031 | 0.040 | [1.958, 2.116] | 3.739 | 0.017 | [3.706, 3.771] | 2.097 | 0.043 | [2.012, 2.179] |
| 7 | 4.190 | 0.016 | [4.158, 4.220] | 2.314 | 0.047 | [2.221, 2.406] | 4.189 | 0.017 | [4.156, 4.222] | 2.516 | 0.063 | [2.393, 2.638] |
| 8 | 4.522 | 0.018 | [4.487, 4.557] | 1.879 | 0.036 | [1.809, 1.950] | 4.522 | 0.018 | [4.488, 4.558] | 2.091 | 0.047 | [1.995, 2.180] |
| 9 | 4.377 | 0.020 | [4.338, 4.417] | 1.600 | 0.031 | [1.533, 1.656] | 4.379 | 0.021 | [4.339, 4.420] | 1.701 | 0.036 | [1.632, 1.771] |
| μξ | 4.316 | 0.202 | [3.901, 4.701] | 4.315 | 0.199 | [3.914, 4.708] | ||||||
| σξ2 | 0.367 | 0.217 | [0.103, 0.751] | 0.366 | 0.219 | [0.113, 0.763] | ||||||
Table 6 Estimates of item parameters for PISA 2012 computer-based mathematics test
| Item | ULRTM | MLRTM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ξ | ω | ξ | ω | |||||||||
| M | SE | 95% CI | M | SE | 95% CI | M | SE | 95% CI | M | SE | 95% CI | |
| 1 | 4.470 | 0.020 | [4.432, 4.508] | 1.617 | 0.031 | [1.558, 1.678] | 4.469 | 0.020 | [4.433, 4.510] | 1.845 | 0.045 | [1.760, 1.936] |
| 2 | 4.630 | 0.019 | [4.592, 4.667] | 1.697 | 0.032 | [1.635, 1.762] | 4.629 | 0.019 | [4.594, 4.668] | 1.976 | 0.051 | [1.874, 2.076] |
| 3 | 4.778 | 0.016 | [4.750, 4.811] | 2.423 | 0.050 | [2.327, 2.519] | 4.778 | 0.015 | [4.747, 4.807] | 2.505 | 0.055 | [2.397, 2.612] |
| 4 | 3.860 | 0.018 | [3.825, 3.895] | 1.866 | 0.036 | [1.793, 1.934] | 3.859 | 0.017 | [3.825, 3.894] | 1.915 | 0.038 | [1.841, 1.991] |
| 5 | 4.258 | 0.016 | [4.226, 4.291] | 2.186 | 0.044 | [2.104, 2.274] | 4.258 | 0.016 | [4.224, 4.287] | 2.202 | 0.047 | [2.112, 2.295] |
| 6 | 3.739 | 0.017 | [3.707, 3.774] | 2.031 | 0.040 | [1.958, 2.116] | 3.739 | 0.017 | [3.706, 3.771] | 2.097 | 0.043 | [2.012, 2.179] |
| 7 | 4.190 | 0.016 | [4.158, 4.220] | 2.314 | 0.047 | [2.221, 2.406] | 4.189 | 0.017 | [4.156, 4.222] | 2.516 | 0.063 | [2.393, 2.638] |
| 8 | 4.522 | 0.018 | [4.487, 4.557] | 1.879 | 0.036 | [1.809, 1.950] | 4.522 | 0.018 | [4.488, 4.558] | 2.091 | 0.047 | [1.995, 2.180] |
| 9 | 4.377 | 0.020 | [4.338, 4.417] | 1.600 | 0.031 | [1.533, 1.656] | 4.379 | 0.021 | [4.339, 4.420] | 1.701 | 0.036 | [1.632, 1.771] |
| μξ | 4.316 | 0.202 | [3.901, 4.701] | 4.315 | 0.199 | [3.914, 4.708] | ||||||
| σξ2 | 0.367 | 0.217 | [0.103, 0.751] | 0.366 | 0.219 | [0.113, 0.763] | ||||||
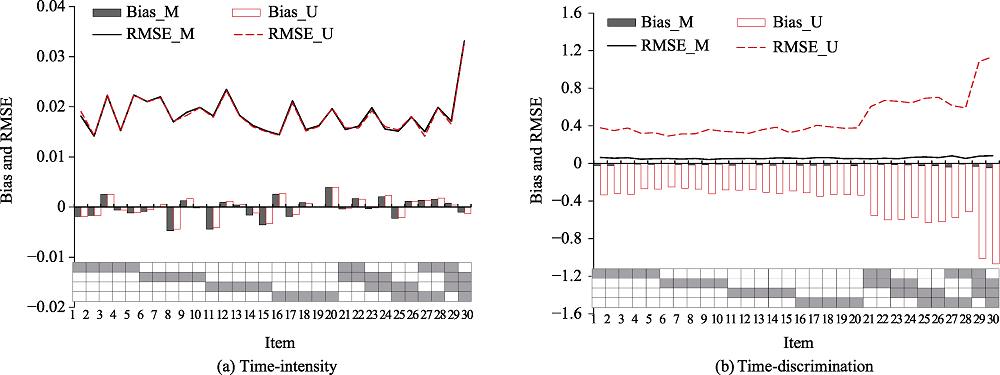
Figure 3. Recovery of item parameters in simulation study 1. Note. U = unidimensional log-normal response time model; M = multidimensional log-normal response time model; RMSE = root mean square error.
| Parameter | MA_bias | M_RMSE | Cor |
|---|---|---|---|
| τ1 | 0.016 | 0.147 | 0.956 |
| τ2 | 0.017 | 0.147 | 0.955 |
| τ3 | 0.016 | 0.144 | 0.957 |
| τ4 | 0.017 | 0.143 | 0.958 |
Table 7 Summaries of the recovery of person parameters in simulation study 1
| Parameter | MA_bias | M_RMSE | Cor |
|---|---|---|---|
| τ1 | 0.016 | 0.147 | 0.956 |
| τ2 | 0.017 | 0.147 | 0.955 |
| τ3 | 0.016 | 0.144 | 0.957 |
| τ4 | 0.017 | 0.143 | 0.958 |
| Στ | τ1 | τ2 | τ3 | τ4 |
|---|---|---|---|---|
| τ1 | 0.00003 (0.00000) | |||
| τ2 | 0.00023 0.00003) | 0.00069 (-0.00010) | ||
| τ3 | 0.00031 (0.00004) | 0.00015 (0.00002) | 0.00015 (0.00002) | |
| τ4 | 0.00015 (0.00002) | 0.00041 (-0.00006) | 0.00020 (0.00003) | 0.00079 (-0.00011) |
Table 8 Recovery of Variance-covariance matrix of person parameters in simulation study 1
| Στ | τ1 | τ2 | τ3 | τ4 |
|---|---|---|---|---|
| τ1 | 0.00003 (0.00000) | |||
| τ2 | 0.00023 0.00003) | 0.00069 (-0.00010) | ||
| τ3 | 0.00031 (0.00004) | 0.00015 (0.00002) | 0.00015 (0.00002) | |
| τ4 | 0.00015 (0.00002) | 0.00041 (-0.00006) | 0.00020 (0.00003) | 0.00079 (-0.00011) |
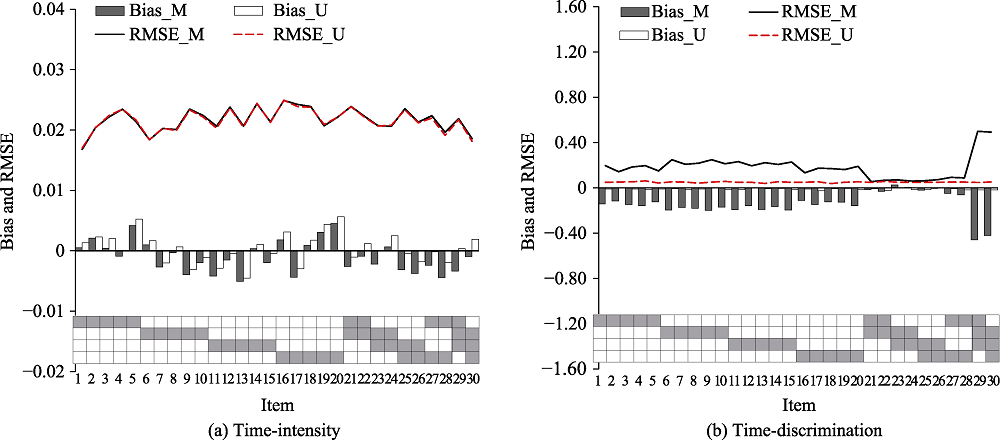
Figure 4. Recovery of item parameters in simulation study 2. Note. U = unidimensional log-normal response time model; M = multidimensional log-normal response time model; RMSE = root mean square error; X-axis is the items; Y-axis is the value of bias and RMSE.
| Analysis model | Parameter | MA_bias | M_RMSE | Cor |
|---|---|---|---|---|
| ULRTM | τ | 0.013 | 0.088 | 0.985 |
| MLRTM | τ1 | 0.023 | 0.197 | 0.974 |
| τ2 | 0.026 | 0.226 | 0.973 | |
| τ3 | 0.027 | 0.235 | 0.971 | |
| τ4 | 0.023 | 0.199 | 0.974 |
Table 9 Recovery of person parameters in simulation study 2
| Analysis model | Parameter | MA_bias | M_RMSE | Cor |
|---|---|---|---|---|
| ULRTM | τ | 0.013 | 0.088 | 0.985 |
| MLRTM | τ1 | 0.023 | 0.197 | 0.974 |
| τ2 | 0.026 | 0.226 | 0.973 | |
| τ3 | 0.027 | 0.235 | 0.971 | |
| τ4 | 0.023 | 0.199 | 0.974 |
| [1] |
Adams, R. J., Wilson, M., & Wang, W. (1997). The multidimensional random coefficients multinomial logit model. Applied Psychological Measurement, 21(1), 1-23.
doi: 10.1177/0146621697211001 URL |
| [2] |
Bolsinova, M., & Tijmstra, J. (2018). Improving precision of ability estimation: Getting more from response times. British Journal of Mathematical and Statistical Psychology, 71(1), 13-38.
doi: 10.1111/bmsp.12104 URL pmid: 28635139 |
| [3] |
Curran, P. J., & Bauer, D. J. (2011). The disaggregation of within- person and between-person effects in longitudinal models of change. Annual Review of Psychology, 62, 583-619.
URL pmid: 19575624 |
| [4] |
de Boeck, P., & Jeon, M. (2019). An overview of models for response times and processes in cognitive tests. Frontiers in Psychology, 10, 102.
doi: 10.3389/fpsyg.2019.00102 URL pmid: 30787891 |
| [5] | Ferrando, P. J., & Lorenzo-Seva, U. (2007). A measurement model for Likert responses that incorporates response time. Multivariate Behavioral Research, 42(4), 675-706. |
| [6] |
Fox, J.-P., & Marianti, S. (2017). Person-fit statistics for joint models for accuracy and speed. Journal of Educational Measurement, 54(2), 243-262.
doi: 10.1111/jedm.12143 URL |
| [7] | Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). Bayesian data analysis. New York: Chapman & Hall. |
| [8] | Goudie, R. J., Turner, R. M., de Angelis, D., & Thomas, A. (2017). MultiBUGS: A parallel implementation of the BUGS modelling framework for faster Bayesian inference. arXiv Preprint arXiv:1704.03216. |
| [9] | Guo, L., Shang, p., & Xia, L. (2017). Advantages and illustrations of application of response time model in psychological and educational testing. Advances in Psychological Science, 25(4), 701-712. |
| [10] |
Guo, X., Luo, Z., & Yu, X. (2020). A speed-accuracy tradeoff hierarchical model based on cognitive experiment. Frontiers in Psychology, 10, 2910.
doi: 10.3389/fpsyg.2019.02910 URL pmid: 31969855 |
| [11] |
Horwitz, B., Tagamets, M. A., & McIntosh, A. R. (1999). Neural modeling, functional brain imaging, and cognition. Trends in Cognitive Sciences, 3(3), 91-98.
doi: 10.1016/s1364-6613(99)01282-6 URL pmid: 10322460 |
| [12] |
Hu, L. T., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal, 6(1), 1-55.
doi: 10.1080/10705519909540118 URL |
| [13] |
Klein Entink, R. H., van der Linden, W. J., & Fox, J.-P. (2009). A Box-Cox normal model for response times. British Journal of Mathematical and Statistical Psychology, 62(3), 621-640.
doi: 10.1348/000711008X374126 URL |
| [14] |
Lu, J., Wang, C., Zhang, J., & Tao, J. (2019). A mixture model for responses and response times with a higher-order ability structure to detect rapid guessing behaviour. British Journal of Mathematical and Statistical Psychology. Online First, https://doi.org/10.1111/bmsp.12175
URL pmid: 31709521 |
| [15] |
Man, K., Harring, J. R., Jiao, H., & Zhan, P. (2019). Joint modeling of compensatory multidimensional item responses and response times. Applied Psychological Measurement, 43(8), 639-654.
doi: 10.1177/0146621618824853 URL pmid: 31551641 |
| [16] | Meng, X.-B. (2016). A log-skew-normal model for item response times. Journal of Psychological Science, 39, 727-734. |
| [17] |
Mesulam, M. M. (1990). Large‐scale neurocognitive networks and distributed processing for attention, language, and memory. Annals of Neurology, 28(5), 597-613.
doi: 10.1002/ana.410280502 URL pmid: 2260847 |
| [18] | Muthén, L. K., & Muthén, B. (2019). Mplus: The comprehensive modeling program for applied researchers: User’s guide, 5. |
| [19] | Ntzoufras, I. (2009). Bayesian modeling using WinBUGS. Manhattan: John Wiley & Sons. |
| [20] | OECD, (2013). PISA 2012 assessment and analytical framework: Mathematics, reading, science, problem solving and financial literacy, OECD Publishing. http://dx.doi.org/10.1787/9789264190511-en |
| [21] | Reckase, M. D. (2009). Multidimensional item response theory. New York: Springer. |
| [22] |
Steiger, J. H. (1990). Structural model evaluation and modification: An interval estimation approach. Multivariate Behavioral Research, 25(2), 173-180.
doi: 10.1207/s15327906mbr2502_4 URL pmid: 26794479 |
| [23] | Tatsuoka, K. K. (1983). Rule Space: An approach for dealing with misconceptions based on item response theory. Journal of Educational Measurement, 20(4), 345-354. |
| [24] | van der Linden, W. J. (2006). A lognormal model for response times on test items. Journal of Educational and Behavioral Statistics, 31(2), 181-204. http://dx.doi.org/10.3102/10769986031002181 |
| [25] | van der Linden, W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items. Psychometrika, 72, 287-308. http://dx.doi.org/10.1007/s11336-006-1478-z |
| [26] | van der Linden, W. J. (2009). Conceptual issues in response- time modeling. Journal of Educational Measurement, 46(3), 247-272. http://dx.doi.org/10.1111/j.1745-3984.2009.00080.x |
| [27] | van der Linden, W. J. (2011). Test design and speededness. Journal of Educational Measurement, 48(1), 44-60. |
| [28] | van der Linden, W. J., Klein Entink, R., & Fox, J.-P. (2010). IRT parameter estimation with response times as collateral information. Applied Psychological Measurement, 34(5), 327-347. |
| [29] |
Wang, C., Chang, H. H., & Douglas, J. A. (2013). The linear transformation model with frailties for the analysis of item response times. British Journal of Mathematical and Statistical Psychology, 66(1), 144-168.
doi: 10.1111/j.2044-8317.2012.02045.x URL pmid: 22506914 |
| [30] |
Wang, C., Weiss, D. J., & Su, S. (2019). Modeling response time and responses in multidimensional health measurement. Frontiers in Psychology, 10, 51.
doi: 10.3389/fpsyg.2019.00051 URL pmid: 30761036 |
| [31] |
Wang, C., & Xu, G. (2015). A mixture hierarchical model for response times and response accuracy. British Journal of Mathematical and Statistical Psychology, 68(3), 456-477.
doi: 10.1111/bmsp.12054 URL pmid: 25873487 |
| [32] | Wang, S., Zhang, S., Douglas, J., & Culpepper, S. (2018). Using response times to assess learning progress: A joint model for responses and response times. Measurement: Interdisciplinary Research and Perspectives, 16(1), 45-58. |
| [33] | Wang, T., & Hanson, B. A. (2005). Development and calibration of an item response model that incorporates response time. Applied Psychological Measurement, 29(5), 323-339. |
| [34] | Zhan, P. (2019). Joint modeling for response times and response accuracy in computer-based multidimensional assessments. Journal of Psychological Science, 42, 170-178. |
| [35] |
Zhan, P., Jiao, H., & Liao, D. (2018). Cognitive diagnosis modelling incorporating item response times. British Journal of Mathematical and Statistical Psychology, 71(2), 262-286.
doi: 10.1111/bmsp.12114 URL pmid: 28872185 |
| [36] | Zhan, P., Jiao, H., Wang, W.-C., & Man, K. (2018). A multidimensional hierarchical framework for modeling speed and ability in computer-based multidimensional tests. arXiv:1807.04003. Available online at: https://arxiv.org/abs/1807.04003 |
| [1] | REN He, CHEN Ping. Two new termination rules for multidimensional computerized classification testing [J]. Acta Psychologica Sinica, 2021, 53(9): 1044-1058. |
| [2] | ZHAN Peida,YU Zhaohui,LI Feiming,WANG Lijun. Using a multi-order cognitive diagnosis model to assess scientific literacy [J]. Acta Psychologica Sinica, 2019, 51(6): 734-746. |
| [3] | LIU Yue, LIU Hongyun. Reporting overall scores and domain scores of bi-factor models [J]. Acta Psychologica Sinica, 2017, 49(9): 1234-1246. |
| [4] | CHEN Ping. Two new online calibration methods for computerized adaptive testing [J]. Acta Psychologica Sinica, 2016, 48(9): 1184-1198. |
| [5] | MENG Xiangbin; TAO Jian; CHEN Shali. Warm’sweighted maximum likelihood estimation of latent trait in the four-parameter logistic model [J]. Acta Psychologica Sinica, 2016, 48(8): 1047-1056. |
| [6] | WANG Wenyi;SONG Lihong;DING Shuliang. Classification accuracy and consistency indices for complex decision rules in multidimensional item response theory [J]. Acta Psychologica Sinica, 2016, 48(12): 1612-1624. |
| [7] | ZHAN Peida; CHEN Ping; BIAN Yufang. Using confirmatory compensatory multidimensional IRT models to do cognitive diagnosis [J]. Acta Psychologica Sinica, 2016, 48(10): 1347-1356. |
| [8] | ZHAN Peida; LI Xiaomin; WANG Wen-Chung; BIAN Yufang; WANG Lijun. The Multidimensional Testlet-Effect Cognitive Diagnostic Models [J]. Acta Psychologica Sinica, 2015, 47(5): 689-701. |
| [9] | YAO Ruosong;ZHAO Baonan;LIU Ze;MIAO Qunying. The Application of Many-Facet Rasch Model in Leaderless Group Discussion [J]. Acta Psychologica Sinica, 2013, 45(9): 1039-1049. |
| [10] | LIU Yue;LIU Hongyun. Comparison of MIRT Linking Methods for Different Common Item Designs [J]. Acta Psychologica Sinica, 2013, 45(4): 466-480 . |
| [11] | DU Wenjiu;ZHOU Juan;LI Hongbo. The Item Parameters’ Estimation Accuracy of Two-Parameter Logistic Model [J]. Acta Psychologica Sinica, 2013, 45(10): 1179-1186. |
| [12] | LIU Hong-Yun,LI Chong,ZHANG Ping-Ping,LUO Fang. Testing Measurement Equivalence of Categorical Items’ Threshold/Difficulty Parameters: A Comparison of CCFA and (M)IRT Approaches [J]. Acta Psychologica Sinica, 2012, 44(8): 1124-1136. |
| [13] | LIU Hong-Yun,LUO Fang,WANG Yue,ZHANG Yu. Item Parameter Estimation for Multidimensional Measurement: Comparisons of SEM and MIRT Based Methods [J]. , 2012, 44(1): 121-132. |
| [14] | TU Dong-Bo,CAI Yan,DAI Hai-Qi,DING Shu-Liang. Parameters Estimation of MIRT Model and Its Application in Psychological Tests [J]. , 2011, 43(11): 1329-1340. |
| [15] | WU Rui,DING Shu-Liang,GAN Deng-Wen. Test Equating with Testlets [J]. , 2010, 42(03): 434-442. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||