1 引言
传统的质性文献综述往往存在“综述者偏差” (Reviewer biases), 为了更加科学、准确地进行知识积累, 元分析(Meta-analysis)得到了越来越广泛的关注和应用(Cheung & Vijayakumar, 2016)。元分析是基于量化统计方法的一种系统性文献述评技术, 其目的在于对特定研究主题的不同研究结果进行整合和比较(Glass, 1976)。近年来, 国内外的元分析发表量增长迅速, 其中元回归模型在调节变量的探索方面得到了十分广泛的应用。通过中国知网检索发现, 从2004年至2019年的15年期间, 以元分析为关键词的人文社科类的中文期刊文献共862篇, 其中82篇使用了元回归模型; 在Education databse、ERIC、PsyARTICLES、Psychology database、PsyINFO、PTSpubd和Research library数据库中进行检索, 从2004年至2019年的15年期间, 标题中包含meta-analysis的英文期刊文献共11698篇, 其中2704篇使用了元回归模型。这些文献的主题涵盖发展与教育、行为治疗、神经成像、语言认知、管理心理学等各个心理学领域。尽管元分析和元回归的相关研究日益增多, 不少实证研究者对于元分析技术的原理、如何有效地获得元分析研究结果等问题仍知之甚浅, 因此有必要对其基本原理及其应用进行深入探讨。
元分析技术的核心和基础在于研究效应的大小, 即效应量(Effect size, ES)。效应量描述了原始研究中变量之间关系的大小和方向(Çoğaltay & Karadağ, 2015), 元分析以原始研究所得的效应量为样本, 效应量个数即样本量。效应量个数的选择是一个成本和效能的权衡过程, 过少的效应量可能会遗漏重要的信息, 降低研究结果的可信度(Cheung & Vijayakumar, 2016), 然而一味地增加效应量并不总能提高统计功效, 还可能导致参数估计的波动(Cohn & Becker, 2003), 同时也对研究可行性提出了较高的要求。
纵览国内外已发表的心理学领域的元分析研究, 实证研究者们纳入的效应量个数参差不齐, 少至20个左右(王超, 袁蒙蒙, 姜媛, 方平, 2019), 多至110个以上(Suchotzki, Verschuere, Bockstaele, Ben-Shakhar, & Crombez, 2017; 刘俊, 秦传燕, 2018); 有学者认为理论上来说两个原始研究就足以开展元分析研究, 但同时也需要注意过少的效应量可能会导致参数估计偏差和错误的结论(Valentine, Pigott, & Rothstein, 2010), Cheung和Vijayakumar (2016)也指出, 基于较少效应量得出的综述性结论很难得到认可, 如果某个领域的原始研究或效应量很少, 也可能说明该领域还不够成熟, 不足以支撑有意义的综述性研究。Viechtbauer, López-López, Sánchez-Meca和Marín-Martínez (2015)的模拟研究结果表明, 在使用包含一个调节变量的简单元回归模型时, 至少需要40个效应量才能保证一定的统计功效, López-López, Noortgate, Tanner-Smith, Wilson和Lipsey (2017)也基于包含一个调节变量的简单元回归模型展开模拟研究, 结果发现多数情境下需要至少80个效应量。可以看出, 尽管理论研究者们对效应量个数的选择进行了一些探索, 但未能得出较为一致的结论。
效应量个数选择是元分析领域十分重要的主题, 但实证研究至今仍然缺少一个公认的效应量个数选择规范, 相关模拟研究也存在不足, 首先是未能在具体的数量选择上得出一致的结论, 其次是目前仅针对包含一个调节变量的简单元回归模型展开讨论, 最后是多数研究者采用的效应量形式是标准均值差(Viechtbauer et al., 2015; López- López et al., 2017), 而不是心理学领域的元分析研究中更为常见的探究变量间相关程度的效应量(如Fisher的Zr), 这不利于为心理学研究者开展元分析实证研究提供指导。
综上, 本文将首先概述元分析技术的基本原理, 在此基础上对元回归模型进行介绍; 然后在前人研究的基础上对调节变量个数进行拓展, 以获得更符合实证研究需求的复杂元回归模型, 进而采用蒙特卡洛模拟对元回归模型的效应量最小个数需求进行探讨。通过操纵效应量个数、调节变量个数、回归系数真值以及研究间剩余异质性的不同水平组合设置多种情境, 并基于统计功效和估计精度对模型的参数估计表现进行评价, 旨在确立效应量最小个数需求, 使实证研究者能够在保证研究结果可靠度的前提下, 尽量提升科研工作的效率。
2 元分析概述
2.1 元分析的目的
元分析技术的主要目的在于:(1)获得普遍性的研究效应大小, 计算总体平均效应量; (2)揭示不同研究结果之间的差异; (3)寻找调节变量阐明研究结果之间差异的来源(Field, 2001)。调节变量(Moderator)指的是对研究结果具有一定解释能力的研究特征变量(Cheung & Vijayakumar, 2016; Schmidt, 2017)。
2.2 元分析模型
2.2.1 基本模型
元分析技术有两类基本模型:固定效应模型(Fixed-effect model)和随机效应模型(Random-effects model)。
假设某一次元分析中纳入了k个原始研究, 得到了k个效应量, 则有固定效应模型:
其中, $y_{i}$ 表示第i个效应量观测值, 共有k个相互独立的效应量; $\theta $表示效应量真值; $ e_{i}$表示第i个研究的抽样变异, 服从正态分布$N(0,v_{i})$。固定效应模型假设不同研究结果之间的变异全部来源于抽样误差, 而这在实际情况中往往不成立, 因此一般不推荐使用固定效应模型(Huizenga, Visser, & Dolan, 2010; Murphy, 2017)。
随机效应模型假设不同研究结果之间的变异由两部分构成:该研究的效应量真值与效应量真值总体的均值之间的变异以及抽样误差(Borenstein, Hedges, Higgins, & Rothstein, 2009, 2010; Viechtbauer, 2010)。公式如下:
其中, $\beta_{0}$表示效应量真值总体的均值; $ u_{i}$表示效应量真值的变异, 即研究间异质性, 服从正态分布$N(0, \tau^2)$。
这两类基本模型的主要目的均在于估计效应量真值(或效应量真值总体的均值), 以获得一个概括性的结果。
2.2.2 元回归
近年来元分析研究者们的重点从仅仅关注效应量真值(某种效应是否存在?)转移到探索效应量的调节变量(在何种情境下这种效应最强?) (López-López et al., 2017; Steel & Kammeyer- Mueller, 2002)。为此, 学者们在元分析基本模型的基础上发展出了元回归。
元回归(Meta-regression), 也称混合效应元回归模型(Mixed-effects meta-regression model), 其通过寻找调节变量, 即研究特征变量(如被试量、被试来源、测量工具类型、量表长度等)来对研究结果之间的差异进行解释(Cafri, Kromrey, & Brannick, 2010; Card, 2012)。公式如下:
元回归可以看作是元分析与回归分析的结合, 其中, 效应量观测值$y_{i}$作为因变量, 调节变量$ x_{i1}L x_{ip}$作为自变量(Viechtbauer et al., 2015)。$\beta_{0}$表示模型截距; $ x_{ip}$表示第i个研究中第p个调节变量的值; $\beta_{p}$表示第p个调节变量的回归系数; $ u_{i}$表示纳入调节变量后的剩余研究间变异, 服从正态分布$N(0, \tau^2)$。
元回归是公认的识别调节变量最合适的方法(López-López et al., 2017; 张天嵩, 刘江波, 钟文昭, 2009), 其既可以处理类别型调节变量也可以处理连续型调节变量, 还支持同时区分多个可能变量, 在国内外元分析研究中得到了广泛应用(Steel & Kammeyer-Mueller, 2002)。
2.3 元分析计算原理
2.3.1 基本模型的计算原理:加权求均值
元分析基本模型的使用遵循“3C”原理:计算(Calculate)每个原始研究的效应量, 转化(Convert)到统一的度量下, 合并(Combine)以获得一个平均效应量(Field, 2001)。元分析研究者对不同原始研究的关键结果信息进行转换, 得到效应量, 然后根据效应量的准确性程度, 对其赋予一定权重, 最后通过数学模型计算总体平均效应的大小, 获得普遍性的结论。
2.3.2 元回归的计算原理:估计和检验回归系数
元回归的重点在于估计回归系数$\beta_{v}$的大小并对$\beta_{v}$进行显著性检验。如果检验的结果显著, 则可以判定$\beta_{v}$所对应的调节变量$x_{iv}$是研究间异质性的来源; 然后计算纳入$x_{iv}$前后, 模型中研究间异质性$\tau^2$的变化比例, 就可以得到$x_{iv}$对研究间异质性的解释比例。
3 模拟研究
3.1 研究问题
纳入多少个效应量是合适的?这是元回归, 乃至元分析的实证研究者们都十分关注的问题。虽然有一些研究进行了探讨, 但仍未能在具体的数量选择上得出一致的结论, 对心理学元分析实证研究的指导有限。本研究拟解决以下问题:第一, 元回归模型达到一定的参数估计要求时效应量的最小个数需求是多少?第二, 当模型包含的调节变量个数不同时, 效应量的最小个数需求是否一致?第三, 元回归模型对于描述相关关系的效应量的适应性如何?
3.2 研究设计
本研究将开展一个蒙特卡洛模拟研究, 通过效应量个数、调节变量个数、回归系数真值以及研究间剩余异质性的不同水平组合设置不同情境, 然后基于统计功效和估计精度对不同情境下元回归模型的参数估计表现进行评价, 从而确立元回归中效应量的最小个数需求。
(1)分析模型。选择心理学元分析研究中最常用的元回归模型为研究对象。已有的模拟研究只关注包含一个调节变量的简单元回归模型(López- López et al., 2017; Steel & Kammeyer-Mueller, 2002; Viechtbauer et al., 2015), 考虑到在实证研究中往往能识别出两个或两个以上有显著解释作用的调节变量, 假设调节效应只存在一个来源是不现实的, 因此有必要对调节变量个数进行拓展。对多个调节变量组合进行考虑不仅能够分离不同调节变量对研究间异质性的贡献, 而且能较好地避免虚假效应(Steel & Kammeyer-Mueller, 2002)。本研究将分别考虑包含一个调节变量的简单模型和包含两个调节变量的复杂模型。
模型一(包含一个调节变量):
模型二(包含两个调节变量):
(2)自变量。①效应量个数k:参考前人研究(López-López et al., 2017; Steel & Kammeyer- Mueller, 2002; Viechtbauer et al., 2015), 令k = 20, 40, 60, 80, 100, 120; ②回归系数真值
(3)其他控制变量。①效应量观测值
(4)结果变量。在不同的模拟条件下, 利用元回归模型(模型一、模型二)对数据集进行估计, 获得回归系数的估计值
(5)参数估计方法和检验方法。参数估计选择常用的加权最小二乘法; 参数显著性检验同时采用Wald-type z检验方法和Knapp and Hartung检验方法, 前者是元分析实证研究常用软件CMA中内置的方法, 后者由Knapp和Hartung (2003)提出, 该方法被证实适用于多数元分析情境(Viechtbauer et.al., 2015)。
3.3 评价指标
除了采用常用的估计精度指标:参数估计偏差和置信区间宽度之外, 本研究创新性地将统计功效确定样本量的方法应用于最小效应量个数的探索, 纳入了统计功效和I类错误率作为评价指标, 共四类评价指标。
其中, 参数估计偏差的计算是用回归系数的估计值减去真值, 再将每个模拟条件下获得的10000个差值结果取均值; 置信区间宽度是用每个条件下得到的参数估计值所对应的95%置信区间上限减去下限取绝对值, 再将该条件下获得的10000个结果取均值; 当回归系数真值不为0时, 每个条件循环10000次得到的95%置信区间中, 不包含0的次数所占的比例就是该条件下的统计功效; 当回归系数真值为0时, 每个条件循环10000次得到的95%置信区间中, 不包含0的次数所占的比例, 即为该条件下的I类错误率(方杰, 张敏强, 2012)。由于模型二中待估计的参数有两个, 此时取两种情况下指标的均值作为每个模拟条件下的指标结果。
3.4 分析工具
本研究的数据生成和参数估计均采用R软件中的metafor程序包(Viechtbauer, 2010)。metafor包操作上简便易懂, 功能强大, 不仅可以同时对多个调节变量进行分析, 还包含多种可供选择的参数估计和检验方法(董圣杰, 曾宪涛, 郭毅, 2012; 张云权, 马露, 冯仁杰, 朱耀辉, 李存禄, 2015)。
4 结果与分析
4.1 参数估计偏差
参数估计偏差小于0.05为宜(López-López et al., 2017; Viechtbauer et al., 2015)。研究结果表明, 在所有模拟条件下参数估计偏差均无超过0.05的, 说明元回归模型总能得到对回归系数的无偏估计, 这与前人的研究结果一致(López-López et al., 2017; Viechtbauer et al., 2015)。也没有观测到调节变量个数、效应量个数、剩余异质性大小对参数估计偏差的大小或方向的明显影响趋势, 因此参数估计偏差的结果仅以附表形式呈现(附表见网络版)。
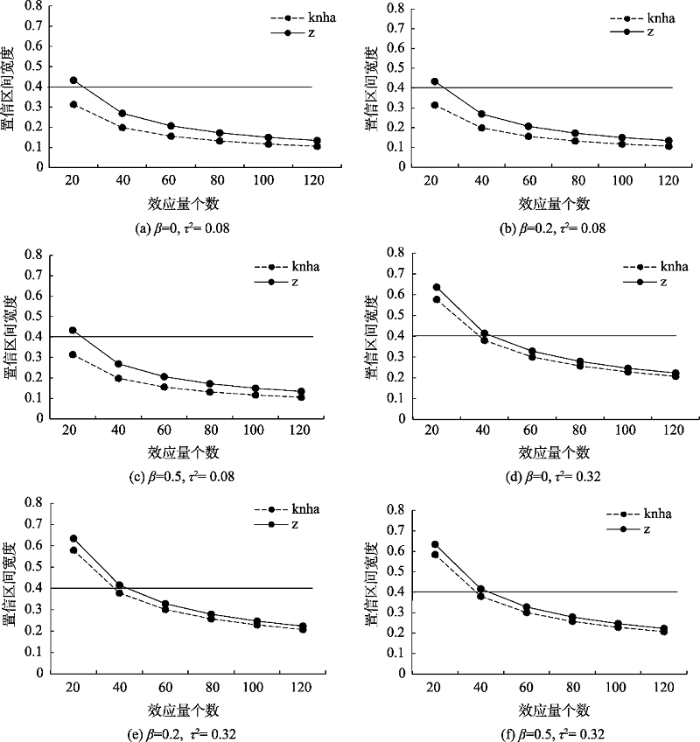
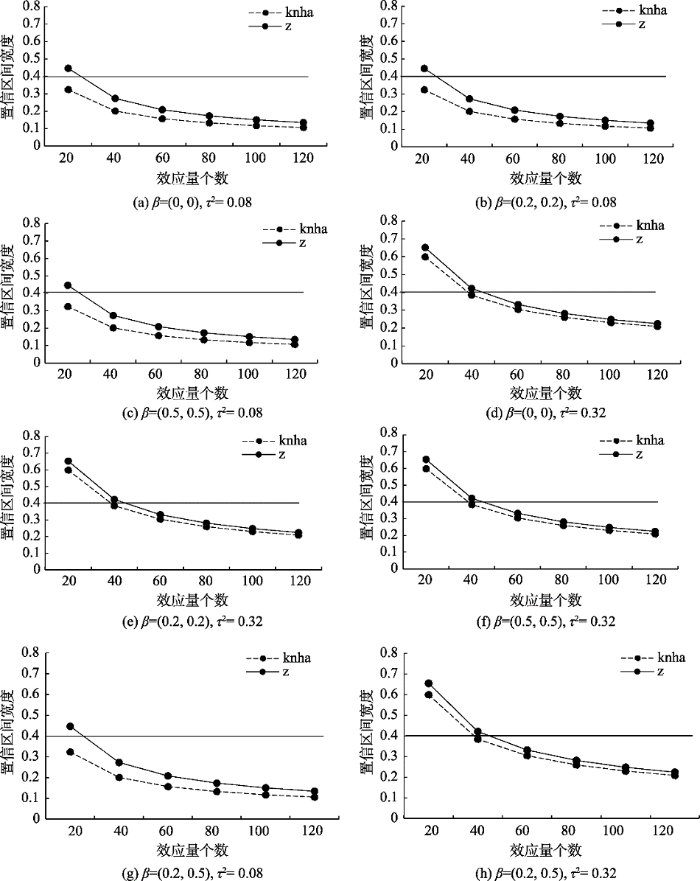
4.2 置信区间宽度
置信区间宽度小于0.4为宜(López-López et al., 2017)。不同模拟情境下的置信区间宽度如附图1、附图2所示(附图见网络版)。
表1 参数估计精度在不同情境下对最小效应量个数的需求(τ2 = 0.08)
| 检验方法 | τ2 = 0.08 | ||||||
|---|---|---|---|---|---|---|---|
| β为0 | β(均)较小 | β(均)较大 | β一个较大, 一个较小 | ||||
| β = 0 | β = (0, 0) | β = 0.2 | β = (0.2, 0.2) | β = 0.5 | β = (0.5,0.5) | β = (0.2,0.5) | |
| Knha-test | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| z-test | 23 | 25 | 23 | 25 | 23 | 25 | 25 |
注:表中数据是根据图中参考线所对应的效应量个数临界值所得, 下同。
表2 参数估计精度在不同情境下对最小效应量个数的需求(τ2 = 0.32)
| 检验方法 | τ2=0.32 | ||||||
|---|---|---|---|---|---|---|---|
| β为0 | β(均)较小 | β(均)较大 | β一个较大, 一个较小 | ||||
| β = 0 | β = (0,0) | β = 0.2 | β = (0.2,0.2) | β = 0.5 | β = (0.5,0.5) | β = (0.2,0.5) | |
| Knha-test | 38 | 38 | 38 | 38 | 38 | 38 | 38 |
| z-test | 43 | 43 | 43 | 43 | 43 | 43 | 43 |
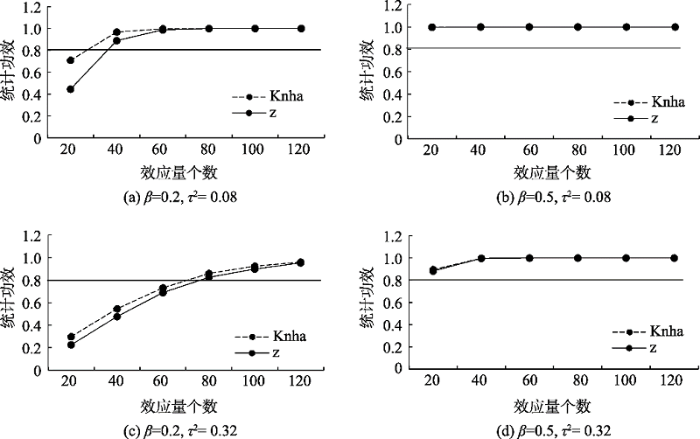
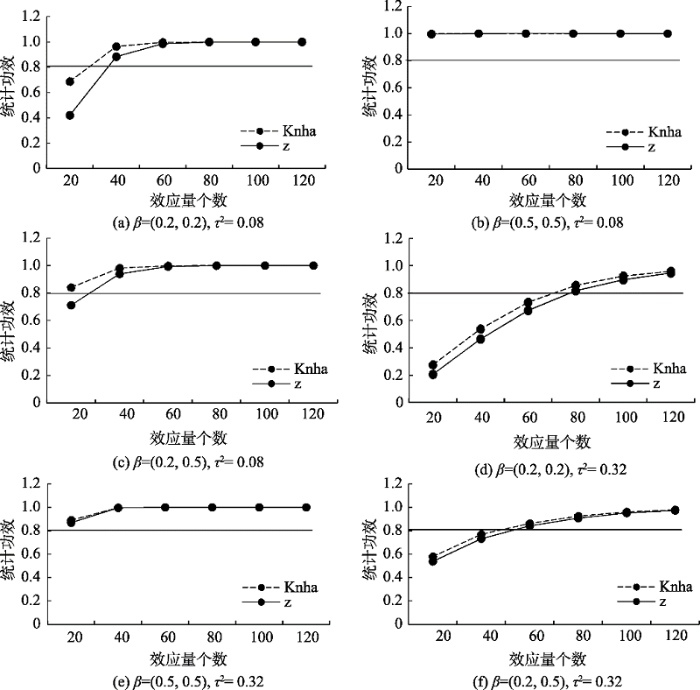
4.3 统计功效
结果表明:①不同情境下, 统计功效均随着效应量个数的增加而不断增加直至稳定, 可以认为在一定范围内效应量个数的增加有利于提升元回归的统计功效。统计功效受到总体效应大小、I类错误率和样本量的影响, 当其他两个条件控制不变时, 提高其中一个因素的水平能够促进统计功效的提升(Valentine et al., 2010), 在元分析中, 效应量个数相当于样本量, 因此提高效应量个数的水平能够促进统计功效的提升; ②同等条件下, 使用Knapp and Hartung检验方法时, 模型达到预期统计功效所需的最小效应量个数一般少于Wald- type z检验方法; ③在不同情境下模型要达到预期统计功效所需的最小效应量个数不同, 详见表3。
表3 统计功效在不同情境下对最小效应量个数的需求
| 检验 方法 | τ2 = 0.08 | τ2 = 0.32 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β(均)较小 | β(均)较大 | β一个较大 一个较小 | β(均)较小 | β(均)较大 | β一个较大 一个较小 | |||||
| β = 0.2 | β = (0.2, 0.2) | β = 0.5 | β = (0.5, 0.5) | β = (0.2, 0.5) | β = 0.2 | β = (0.2, 0.2) | β = 0.5 | β = (0.5, 0.5) | β = (0.2, 0.5) | |
| Knha-test | 30 | 30 | √ | √ | 20 | 70 | 70 | 20 | 20 | 50 |
| z-test | 38 | 38 | √ | √ | 30 | 80 | 80 | 20 | 20 | 52 |
注:√表示该情况下总能满足预期参数估计要求, 如当τ2 = 0.08, β = 0.5时总能达到0.8的预期统计功效。
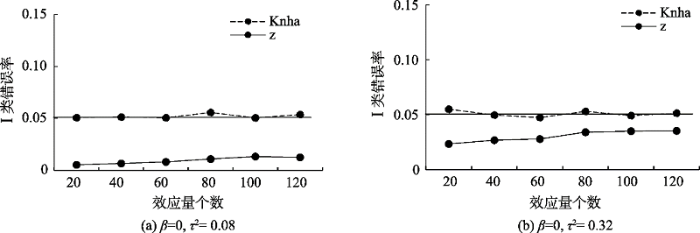
4.4 I类错误率
结果表明, 纳入更多的效应量一定程度上可以改善Wald-type z检验方法对I类错误率的控制, 但仍明显低于设定值(0.05), 尤其是在剩余异质性较小的情况下; 而Knapp and Hartung检验方法在不同条件下的I类错误率均非常接近设定值, 即相比于Wald-type z检验方法, Knapp and Hartung检验方法对I类错误率的控制能力更好, 这与López-López等人(2017)的研究结果一致。
表4 不同情境下模型对最小效应量个数的总体需求(Knapp and Hartung检验方法)
| 回归系数取值 | 剩余异质性较小 | 剩余异质性较大 | ||
|---|---|---|---|---|
| 包含一个调节变量 | 包含两个调节变量 | 包含一个调节变量 | 包含两个调节变量 | |
| β(均)为0 | 20 | 20 | 38 | 38 |
| β(均)较小 | 30 | 30 | 70 | 70 |
| β(均)较大 | 20 | 20 | 38 | 38 |
| β1较小β2较大 | —— | 20 | —— | 50 |
表5 不同情境下模型对最小效应量个数的总体需求(Wald-type z检验方法)
| 回归系数取值 | 剩余异质性较小 | 剩余异质性较大 | ||
|---|---|---|---|---|
| 包含一个调节变量 | 包含两个调节变量 | 包含一个调节变量 | 包含两个调节变量 | |
| β(均)为0 | 23 | 25 | 43 | 43 |
| β(均)较小 | 38 | 38 | 80 | 80 |
| β(均)较大 | 23 | 25 | 43 | 43 |
| β1较小β2较大 | —— | 30 | —— | 52 |
总的来看, 回归系数的真值较小时, 所需的效应量较多。因此, 在开展元回归研究之前, 研究者可以根据已有的实证或理论研究对回归系数的大小范围进行预估, 进而判断效应量个数的最低要求; 此外, 同等条件下, 剩余异质性越大, 所需的效应量越多。这反映了在元回归研究过程中探索调节变量的重要性, 因为当纳入了合适的调节变量时, 研究间异质性就可以得到有效的解释, 剩余异质性就会降低, 此时效应量个数需求也会降低。
5 讨论
本研究基于心理学常用的效应量Fisher的Zr对元回归模型行探索, 一方面验证了元回归模型对该效应量的适应性, 另一方面建立了元回归模型中效应量最小个数需求的规范, 进而比较了最小效应量个数需求在包含一个、两个调节变量的模型中的差别, 以及不同检验方法对最小效应量个数需求和模型参数估计的影响。研究结果弥补了现有研究的不足, 同时为元回归在心理学领域的推广应用提供了理论支撑和实质性的参考。
5.1 元回归模型对Fisher的Zr的适应性
在本研究中, 元回归模型总能得到对参数的无偏估计, 也没有观测到其他变量对参数估计偏差大小或方向的明显影响趋势。结果表明元回归模型能够较好地适应心理学元分析实证研究中常用的Fisher的Zr这一效应量, 这为元回归分析在心理学领域的推广应用提供了理论支撑。
5.2 元回归模型的效应量最小个数需求
研究结果表明, 元回归模型需要足够数量的效应量以达到参数估计要求。有学者指出, 过少的效应量可能会遗漏重要的信息, 降低研究结果的可信度, 得出的综述性结论也很难得到认可(Cheung & Vijayakumar 2016), 这与本研究的研究结果是一致的。为达到参数估计要求, 研究者至少需要纳入20个效应量, 且应当根据实际情况进一步增加效应量个数。
同等条件下, 剩余异质性较大、回归系数真值较小时所需的效应量较多。因此, 研究者在研究开始前应当对回归系数的大小范围进行预估, 进而对效应量的个数需求有基本的判断, 在研究过程中则需要积极探索合适的调节变量以降低剩余异质性。
5.3 调节变量个数对效应量最小个数需求的影响
在本研究中, 最小效应量个数需求在包含一个、两个调节变量的模型中差别不大。采用Knapp and Hartung检验方法时, 包含一个、两个调节变量的元回归模型在不同情境下的效应量最小个数需求相同; 采用Wald-type z检验方法时, 两种元回归模型在不同情境下的效应量最小个数需求也基本一致。未来研究可进一步增加调节变量个数, 深入探索调节变量个数对效应量最小个数需求的影响。
5.4 参数检验方法的比较
研究结果表明, 同等条件下, 相比于Knapp and Hartung检验方法, 使用Wald-type z检验方法时, 元回归模型对I类错误率的控制较差, 且达到预期统计功效和参数估计精度时所需的最小效应量个数一般较多。
López-López等人(2017)对仅包含一个调节变量的简单元回归模型进行研究, 结果表明了Wald- type z检验方法对I类错误率的控制能力较差, 本研究通过拓展调节变量的个数, 得到基于复杂元回归模型的研究结果, 进一步证实了Wald-type z检验方法在控制I类错误率方面的不足。目前国内心理学元分析研究者多使用CMA软件, 而该软件仅支持Wald-type z检验方法, 考虑到Wald- type z检验方法犯I类错误的概率往往偏大, 已发表的元分析研究中许多显著结果是有待进一步商榷的。未来的元分析研究者也应慎重使用CMA软件。
5.5 不足与展望
本研究仍存在一些有待改进的地方。由于目前缺少对效应量相依性(Dependence)程度的划分标准以及公认的处理方法, 本研究中暂未讨论相依性问题, 仍依据基本模型假设每个原始研究仅提取一个效应量。相依性是指, 当同一个研究中采用多种量表对同一批被试施测或者对同一批被试重复施测时, 同一个研究就能够提取多个效应量, 此时效应量之间就会存在相关(López‐López et al., 2017)。未来研究可对效应量的相依性程度划分进行探究, 进而探讨当存在不同程度的相依性时效应量的最小个数需求。
6 结论与建议
6.1 结论
(1)元回归模型能够较好地适应Fisher的Zr这一效应量;
(2)为达到参数估计要求, 元回归分析至少需要20个效应量, 且应当根据实际情况进一步增加。纳入合适的调节变量能降低对效应量的个数需求;
(3)效应量的最小个数需求在包含一个、两个调节变量的模型中差别不大;
(4) Wald-type z检验方法在元回归分析中易犯I类错误。
6.2 建议
基于研究结果, 下面总结了几点建议。
(1)元回归模型可以成为整合和比较心理学领域研究结果的有效工具;
(2)实证研究者应慎重采用内嵌Wald-type z检验方法的CMA软件, 推荐使用R软件的metafor包及其中的Knapp and Hartung检验方法;
(3)实证研究至少需要20个效应量, 且应当根据实际情况进一步增加效应量个数。在研究开始前, 研究者应对回归系数的大小范围进行预估, 在研究过程中则需要探索合适的调节变量以降低剩余异质性。采用Knapp and Hartung检验方法的情况下, 当剩余异质性较小且回归系数(均)较小时需增至30个效应量; 当剩余异质性较大时, 效应量增至38个可满足要求, 此时若回归系数一个较大一个较小需增至50个效应量, 若回归系数(均)较小需增至70个;
(4)这几点建议可以对未来审稿人在评估一个元回归研究的质量时提供参考, 有助于考察该研究是否纳入了足够的效应量个数以获得稳定可信的结果。
附录1
参数估计偏差:
附表1 包含一个调节变量时不同效应量个数下的参数估计偏差(knha-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||
|---|---|---|---|---|---|---|
| β = 0 | β = 0.2 | β = 0.5 | β = 0 | β = 0.2 | β = 0.5 | |
| 20 | -0.0004 | -0.0001 | 0.0003 | -0.0012 | 0.0008 | 0.0056 |
| 40 | 0.0009 | 0.0004 | -0.0001 | -0.0031 | -0.0011 | -0.0009 |
| 60 | 0.0006 | 0.0000 | -0.0009 | 0.0010 | -0.0014 | -0.0009 |
| 80 | 0.0004 | -0.0003 | -0.0003 | 0.0000 | 0.0003 | -0.0005 |
| 100 | -0.0007 | 0.0000 | 0.0002 | -0.0006 | 0.0004 | 0.0000 |
| 120 | 0.0000 | 0.0000 | -0.0004 | 0.0003 | -0.0001 | 0.0002 |
附表2 包含一个调节变量时不同效应量个数下的参数估计偏差(z-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||
|---|---|---|---|---|---|---|
| β = 0 | β = 0.2 | β = 0.5 | β = 0 | β = 0.2 | β = 0.5 | |
| 20 | 0.0000 | 0.0000 | 0.0003 | 0.0026 | 0.0005 | -0.0009 |
| 40 | 0.0007 | 0.0004 | -0.0009 | 0.0000 | -0.0004 | 0.0003 |
| 60 | -0.0003 | 0.0007 | -0.0001 | -0.0005 | 0.0000 | 0.0003 |
| 80 | 0.0000 | 0.0001 | 0.0008 | 0.0001 | 0.0013 | 0.0017 |
| 100 | -0.0002 | 0.0001 | -0.0001 | 0.0005 | -0.0009 | -0.0014 |
| 120 | 0.0001 | 0.0003 | -0.0006 | 0.0007 | 0.0000 | 0.0002 |
附表3 包含两个调节变量时不同效应量个数下的参数估计偏差(knha-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||||
|---|---|---|---|---|---|---|---|---|
| β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | |
| 20 | -0.0008 | 0.0006 | -0.0007 | 0.0003 | 0.0001 | -0.0007 | 0.0003 | -0.0005 |
| 40 | 0.0003 | 0.0006 | -0.0001 | 0.0008 | -0.0008 | 0.0001 | -0.0017 | -0.0005 |
| 60 | 0.0000 | -0.0006 | -0.0003 | 0.0000 | 0.0004 | 0.0001 | 0.0003 | -0.0002 |
| 80 | 0.0001 | 0.0002 | -0.0004 | 0.0001 | 0.0005 | 0.0005 | 0.0006 | 0.0001 |
| 100 | -0.0002 | 0.0002 | -0.0003 | 0.0001 | 0.0004 | 0.0006 | -0.0003 | 0.0002 |
| 120 | 0.0000 | 0.0001 | 0.0001 | -0.0001 | -0.0003 | 0.0000 | 0.0002 | 0.0004 |
附表4 包含两个调节变量时不同效应量个数下的参数估计偏差(z-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||||
|---|---|---|---|---|---|---|---|---|
| β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | |
| 20 | -0.0003 | -0.0002 | 0.0009 | 0.0006 | 0.0005 | -0.0002 | 0.0000 | 0.0000 |
| 40 | -0.0008 | -0.0001 | 0.0000 | -0.0002 | 0.0002 | -0.0002 | 0.0002 | 0.0010 |
| 60 | 0.0001 | -0.0002 | -0.0004 | -0.0001 | 0.0010 | 0.0002 | 0.0005 | 0.0001 |
| 80 | 0.0000 | -0.0003 | -0.0001 | 0.0002 | 0.0005 | -0.0002 | -0.0001 | 0.0001 |
| 100 | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0006 | -0.0003 | 0.0000 | 0.0002 |
| 120 | 0.0001 | 0.0002 | 0.0005 | -0.0001 | 0.0005 | 0.0005 | 0.0000 | 0.0004 |
附录2
附图1
附图2
附图3
附图4
附图5
附图6
附录3
R语句
#以模型一(仅包含一个调节变量)为例#
install.packages ("metafor")
library (metafor)
K<-20 #设定效应量个数K, 有6种取值20, 40, 60, 80, 100, 120
β<-0.0 #设定回归系数真值, 有3种取值0, 0.2, 0.5
#需要生成两个回归系数时, 添加下标即可, 如β_m<-0, β_n<-0
tau2<-0.08 #设定剩余异质性, 有两种取值0.08, 0.32
output<-list(id = NULL, beta1 = NULL, beta2 = NULL, ci.lb2 = NULL, ci.ub2 = NULL)
for (i in 1:10000){
output$\$ $id<-append (output$\$ $id, i)
nn<-rlnorm (K, meanlog = 1, sdlog = 0.9)
n<- round (nn*K) #生成被试量n
n[n<25]<-25
n[n>1000]<-1000
vv<-1/(n-3)
vi<-sqrt(vv)
e<-rnorm (K, mean = 0, sd = sqrt(vv + tau2))
xi<-rnorm (K) #生成调节变量x
yi<-0+xi*β+e #通过元回归模型一生成因变量y, 其中截距固定为0
#拟合元回归函数, 获得回归系数估计值
out<-rma.uni (yi, vi, mods = ~xi, tau2 = tau2, test = "knha", method = "DL") #test指定了检验方法
output$\$ $beta1<-append (output$\$ $beta1, out$\$ $b[1])
output$\$ $beta2<-append (output$\$ $beta2, out$\$ $b[2])
output$\$ $ci.lb2<-append (output$\$ $ci.lb2, out$\$ $ci.lb[2])
output$\$ $ci.ub2<-append (output$\$ $ci.ub2, out$\$ $ci.ub[2])
write.table (output, "D:/20-0.0-0.08.txt")
}
参考文献
Introduction to meta-analysis
A basic introduction to fixed-effect and random-effects models for meta-analysis
A meta-analysis: Empirical review of statistical power, type I error rates, effect sizes, and model selection of meta-analyses published in psychology
A guide to conducting a meta-analysis
How meta-analysis increases statistical power
Meta-analysis of correlation coefficients: A Monte Carlo comparison of fixed- and random-effects methods
Primary, secondary, and meta-analysis of research
Testing overall and moderator effects in random effects meta-regression
Improved tests for a random effects meta-regression with a single covariate
Assessing meta- regression methods for examining moderator relationships with dependent effect sizes: A Monte Carlo simulation
What inferences can and cannot be made on the basis of meta-analysis?
Statistical and measurement pitfalls in the use of meta-regression in meta-analysis
Comparing meta-analytic moderator estimation techniques under realistic conditions
Lying takes time: A meta-analysis on reaction time measures of deception
How many studies do you need? A primer on statistical power for meta-analysis
Conducting meta-analyses in R with the metafor package
A comparison of procedures to test for moderators in mixed-effects meta-regression models