以Binet和Simon (1904)的开创性工作为起点, 项目反应理论(Item Response Theory, IRT)经过百余年发展, 已广泛用于题目的标定与分析、被试的拟合与评分、测验的设计以及大规模教育评价等领域中(van der Linden, 2018), 是心理与教育测量领域最为重要的分析方法之一。虽然研究者针对作答评分、测验维度以及层级数据(hierarchical data)等实际问题提出一系列不同的模型并拓展IRT的应用情境, 但是绝大部分IRT模型只能刻画被试与题目之间的关系, 限制了IRT模型在心理与教育研究中的应用。

本文将基于广义线性混合模型(Generalized Linear Mixed Models, GLMM)和非线性混合模型(Nonlinear Mixed Models, NLMM)构建的IRT模型, 定义为解释性项目反应理论模型(Explanatory IRT Models, EIRTM; De Boeck & Wilson, 2004)。EIRTM是一个综合的解释性模型框架, 它允许在IRT模型的基础上加入预测变量, 在刻画被试和题目间关系的基础上, 进一步解释相关变量影响, 因而拓展IRT模型的应用范围。EIRTM之所以重要, 主要有以下几个方面的原因：

首先, EIRTM摆脱传统IRT模型的限制, 它不仅是测量模型, 而且被称为解释性测量(explanatory measurement)模型。EIRTM能够将题目特征和被试特征纳入模型并解释作答反应如何受到这些变量的影响, 所以EIRTM可用于处理各种测量准确性问题：比如, 题目位置效应(Item Position Effect, IPE)、测验模式效应(Test Mode Effect, TME)、题目功能差异(Differential Item Functioning, DIF)以及局部依赖(Local Dependencies, LD)等等。

其次, EIRTM提出一个综合的模型构建观点。现有的IRT模型采用不同的术语标注和建模方法, 使得研究者很难意识到IRT模型之间存在的共性(Rabe-Hesketh & Skrondal, 2016)。但是, 绝大部分IRT模型实际上可以等价地构建为GLMM和NLMM的形式¹ (1 不包括以三参数逻辑斯蒂克模型(Birnbaum, 1968)为代表的混合模型(mixture models)。) (De Boeck & Wilson, 2004, 2016; Rijmen, Tuerlinckx, De Boeck, & Kuppens, 2003)。另外, EIRTM体现IRT和回归分析的统一, 是一个更为广义的分析框架。广义线性模型(Generalized Linear Models, GLM)涵盖以logit回归、probit回归和基本线性模型(basic linear models)为代表的常用回归模型(Gill, 2000), 而且GLM和大部分IRT模型都是GLMM和NLMM的特例(Stroup, 2012)。因此通过引入EIRTM的框架, 研究者能够将回归模型和IRT模型涵盖在一个更为广义的分析框架之下, 从而形成更为完备的统计测量观。

最后, 应用EIRTM的最大优势在于对预测变量的直接建模和估计, 即“一步法”。虽然在实际应用中也可以采用“两步法”进行分析(即第一步先使用IRT模型得到不同测验情境² (2 不同的测验情境是指不同的题本、不同的被试群体或者不同的测验形式等等, 本质上就是IRT研究中的多组分析(multiple group analysis)。)的参数估计值; 第二步再对不同情境得到的参数估计值进行显著性检验, 或者以参数估计值为因变量进行回归分析), 但是“一步法”要优于“两步法”：(1)“两步法”容易低估测量误差, 尤其是第一步分析中产生的测量误差经常会被忽视, 从而导致犯第一类错误的概率增大(刘红云, 骆方, 2008); (2) 相比于事先采用等组设计或事后采用多组比较的“两步法”, 采用“一步法”的EIRTM更为简便、也能处理更复杂的情况(Debeer & Janssen, 2013); (3) 使用EIRTM可将预测变量的效应与题目难度、被试能力分离, 这有助于对预测变量进行分析和解释(聂旭刚, 陈平, 张缨斌, 何引红, 2018)。

综上, EIRTM提供一个灵活且综合的解释性模型框架。在EIRTM中, 研究者可以自主地构建研究所需要的IRT模型, 从而更好地解释数据。鉴于EIRTM的理论意义与应用价值, 本文将简单介绍EIRTM的基本理论并着重介绍EIRTM的应用情况, 以期能够帮助读者更加深入地了解和使用EIRTM。本文将按以下顺序进行组织：第2节概述EIRTM的基本概念以及参数估计方法; 第3节介绍如何使用EIRTM解决测量准确性问题; 第4节将提供一个具体例子对EIRTM的使用进行说明; 第5节讨论EIRTM的不足之处以及今后的研究方向。

因为GLMM本质上是回归模型的拓展, 所以为了更好地理解GLMM, 先简单引入线性回归模型(linear regression model)：

其中p代表被试, i表示处理, ${{\beta }_{0}}$为截距, ${{\beta }_{1}}$为斜率, ${{X}_{i}}$为预测变量的值, ${{\varepsilon }_{pi}}$为残差。GLMM是线性回归模型的一般形式。下面将具体介绍GLMM及NLMM。

在预测变量与观测值建立连接之前使用连接函数(link function)进行转换的模型, 即GLM。GLM实际上就是经典回归模型的普遍化, 之所以称为“广义(generalized)”是因为连接函数可以任意选取。公式(1)所示的线性回归模型即用线性函数连接预测变量和观察值, 即本身连接函数(identity link function)。如果GLM中还包含随机效应(random effect), 那么模型就被称为GLMM (Stroup, 2012)。随机效应是指预测变量的效应不是一个常数, 而是来源于一个概率分布, 具有期望和方差³ (3 在IRT模型中引入随机效应看似不常见, 但EM算法的最大边际似然估计(Maximum Marginal Likelihood Estimation with EM, MMLE/EM)就是将伴随参数(incidental parameter, 即能力参数)视为随机效应(Bock & Aitkin, 1981; Bock & Lieberman, 1970)。); 与之对应的是固定效应(fixed effect), 是指预测变量的效应是一个常数, 没有测量误差⁴ (4 这些概念经常用于多层线性模型(Hierarchical Linear Model, HLM)中。本质上, 随机效应对应的随机系数回归方法(random coefficients approach)也被称为分层回归方法或多水平回归方法(hierarchical or multilevel regression approach)。)。在公式(1)中, 截距${{\beta }_{0}}$和斜率${{\beta }_{1}}$都是固定效应。

GLMM由三个部分组成(De Boeck & Wilson, 2004)：

(1) 随机成分(random component), 即观测变量及其期望的分布函数, 对应IRT中被试p在题目i上的作答反应${{Y}_{pi}}$及其均值${{\mu }_{pi}}$的分布函数。当作答反应为二分时, 其分布函数为独立的伯努利分布(Bernoulli distribution), 记为${{Y}_{pi}}\tilde{\ }$$\text{Bernoulli(}{{\pi }_{pi}})$, 其中${{\pi }_{pi}}$表示被试p在题目i上的正确作答概率$P\left( {{Y}_{pi}}=1 \right)$且${{\mu }_{pi}}={{\pi }_{pi}}$。

(2) 连接函数, 即用于连接观测变量的期望${{\pi }_{pi}}$和系统成分${{\eta }_{pi}}$, 记为${{\eta }_{pi}}={{f}_{link}}\left( {{\pi }_{pi}} \right)$, 其中${{f}_{link}}\left( \cdot \right)$表示连接函数。在IRT领域中, 可以使用probit连接函数和logit连接函数, 它们分别对应正态肩形模型(normal-ogive models)和逻辑斯蒂克模型(logistic models)。

(3) 系统成分(systematic component), 即预测变量的线性函数, 记为${{\eta }_{pi}}$。在GLMM中, 预测变量可以分为两类, 具有固定效应${{\beta }_{q}}$的预测变量${{X}_{iq}}$和具有随机效应${{\theta }_{pj}}$的预测变量${{Z}_{ij}}$：

(5公式(2)是基于IRT模型改写的：(1) 此处$\underset{q=1}{\overset{Q}{\mathop \sum }}\,{{\beta }_{q}}{{X}_{iq}}$对应题目i的难度${{\beta }_{i}}$ ($\underset{q=1}{\overset{Q}{\mathop \sum }}\,{{\beta }_{q}}{{X}_{iq}}={{\beta }_{i}}$), 即${{\beta }_{q}}={{\beta }_{i}}$。此表达没有截距, 也就是忽略${{\beta }_{q}}$的均值${{\beta }_{0}}$; (2) 另一种常见写法是\[\underset{j=1}{\overset{J}{\mathop \sum }}\,{{\theta }_{pj}}{{Z}_{ij}}+\underset{q=1}{\overset{Q}{\mathop \sum }}\,{{{\beta }'}_{q}}{{X}_{iq}}\], 其中的$\underset{q=1}{\overset{Q}{\mathop \sum }}\,{{{\beta }'}_{q}}{{X}_{iq}}$可以理解为题目容易度(item easiness); (3) 还有一种写法是将第一题作为参照题, 截距为${{\beta }_{0}}$, 下标从0开始直到q-1结束, 而且${{\beta }_{0}}+{{\beta }_{q-1}}={{\beta }_{i}}$, 这种写法多用于多水平IRT模型。)

其中i对应题目, p对应被试; Q和J分别()表示固定效应${{\beta }_{q}}$和随机效应${{\theta }_{pj}}$的个数, ${{X}_{iq}}$和${{Z}_{ij}}$为预测变量。此处假设${{X}_{iq}}$为题目的指示变量(indicator variable), 即题目的虚拟编码(dummy code)变量, 当i = q时, ${{X}_{iq}}$ = 1, 当i ≠ q, ${{X}_{iq}}$ = 0; ${{Z}_{ij}}$同理, 也可视为维度的指示变量。记${{\theta }_{p}}={{\left( {{\theta }_{p1}},{{\theta }_{p2}},\cdots ,{{\theta }_{pJ}} \right)}^{T}}$, 有${{\theta }_{p}}\tilde{\ }N\left( 0,\mathbf{\Sigma } \right)$, 即${{\theta }_{p}}$服从均值向量为0、协方差矩阵为$\mathbf{\Sigma }$的多元正态分布⁶ (6据此, 公式(2)可以表示成更简洁的矩阵形式：
x${{\eta }_{p}}=$ $X\beta +Z{{\theta }_{p}}$。虽然矩阵形式在统计领域更为常见, 但考虑到解释的便利和研究的实际, 本文统一使用指示变量(虚拟变量)组织公式。)。在GLMM中, ${{\eta }_{pi}}$只由线性成分构成, 对应Rasch模型簇。但是对于包含区分度参数的IRT模型来说, 还包括非线性成分(参数相乘), 属于NLMM7 (7 其实也可以说, GLMM是NLMM的特例(Rijmen et al, 2003), 因为NLMM既能刻画非线性关系又能描述线性关系。)。因此, 通过GLMM和NLMM构建EIRTM, 就能从更一般的视角拓展IRT模型, 详见第4节的EIRTM实例部分。

EIRTM的参数估计方法有很多, 但都涉及复杂的统计知识, 此处仅做简单介绍：(1)全似然分析(full-likelihood analysis), 即对EIRTM的边际似然函数进行数值逼近(numerical approximation)以求得估计值使边际似然函数达到最大值。此类方法包括高斯-厄尔米特求积(Gauss-Hermite quadrature)与蒙特卡罗积分(Monte Carlo integration)等直接最大法[对应的统计软件(包)为SAS PROC NLMIXED (SAS Institute, 2015)、STATA的GLLAMM (Rabe-Hesketh, Skrondal, & Pickles, 2004)和HLM (Raudenbush, Bryk, Cheong, Congdon Jr, & Toit, 2011)]以及使用EM算法的间接最大法[对应的软件有MULTILOG (Thissen, 1991)和ConQuest (Adams, Wu, & Wilson, 1988)]; (2)线性分析近似(linearized analytical approximations), 即对EIRTM的边际似然函数中含有的积分求近似解, 包括拉普拉斯近似(Laplace approximation)、带惩罚的拟似然法(Penalized Quasi-Likelihood Method, PQL)和边际拟似然法(Marginal Quasi-Likelihood Approach, MQL), 对应的软件(包)有R语言的lme4包(Bates, Mächler, Bolker, & Walker, 2015)、HLM和SAS PROC GLIMMIX (SAS Institute, 2015); (3)贝叶斯方法, 即采用马尔科夫链蒙特卡洛 (Markov chain Monte Carlo, MCMC)方法, 典型的分析软件有OpenBUGS (Spiegelhalter, Thomas, Best, & Lunn, 2014)。更详细的算法介绍与比较可以参见Bolker等(2009)的综述。

目前尚未发现不同方法得到的估计结果之间会存在显著差异。(De Boeck和Wilson (2004)对6种统计软件的估计结果进行比较, 发现差异不大, 而且采用同一类估计方法的软件的估计结果更加接近。(Jeon, Rijmen和Rabe-Hesketh (2013)基于模拟数据对WinBUGS⁸ (8上文所述的OpenBUGS是WinBUGS的后续开源版本, 两者几乎相同, 详见https://www.mrc-bsu.cam.ac.uk/software/bugs/。)、PROC NLMIXED、GLLAMM以及含逻辑斯蒂回归节点的贝叶斯网络(Bayesian Networks with Logistic Regression Nodes, BNL; Rijmen, 2006)进行比较, 结果发现：不同软件估计的结果相似, 差别在于BNL的估计速度远快于其他软件。另外, Jeon, Rijmen和Rabe-Hesketh (2014)还在BNL的基础上, 开发了R语言的FLIRT包。总之, 目前用于分析EIRTM的软件种类繁多, 但是不同软件估计结果接近, 研究者可以根据自己的需要进行选择。

IPE是指同一个题目在不同测验间因题目位置的变化而导致题目参数的变化(聂旭刚等人, 2018)。IPE违背了IRT的参数不变性(parameter invariance)特征, 使得基于IRT的测验公平性分析、计算机化自适应测验(Computerized Adaptive Testing, CAT)以及矩阵抽样设计(matrix sampling design)等重要应用都受到影响。因此, 很有必要对IPE进行检测及解释。

用于检测IPE的EIRTM可以分为三类(聂旭刚等人, 2018)：第1类模型记为模型IPE-1 (Hohensinn, Kubinger, Reif, Schleich, & Khorramdel, 2011)：

其中p表示被试, i表示题目($i=1,2,\cdots ,I$), q表示变量(q=1,2,...,Q), 且Q = I; ${{\theta }_{p1}}$为能力参数,${{\theta }_{p1}}\tilde{\ }N\left( 0,\text{ }\!\!\sigma\!\!\text{ }_{{{\theta }_{p1}}}^{2} \right);{{X}_{iq}}$为指示变量, 当i = q时, ${{X}_{iq}}=1$,否则取0; $\underset{q=1}{\overset{Q}{\mathop \sum }}\,{{\beta }_{q}}{{X}_{iq}}$如前文所述, 对应题目难度; $\gamma $表示的是IPE。此时$\gamma $为固定效应, 它只与题目位置k有关, 所有题目在同一位置的难度变化都相同9 (9 此处仅假设IPE为线性变化, 更复杂的非线性情况可以表示为k的二次函数等(参见Kang, 2014; Trendtel & Robitzsch, 2018))。此模型本质上是对题目难度进行分解, 从而得出IPE。

第2类模型记为模型IPE-2 (Debeer & Janssen, 2013)：

注意此处${{\gamma }_{i}}=\gamma +{{{\gamma }'}_{i}},{{{\gamma }'}_{i}}$被定义为随机效应, ${{{\gamma }'}_{i}}\tilde{\ }$ $N\left( 0,\text{ }\!\!\sigma\!\!\text{ }_{{{{{\gamma }'}}_{i}}}^{2} \right)$, 其余参数含义同上。此模型假设IPE受题目的影响, 即不同题目在同一位置上的难度变化不同。

第3类模型记为IPE-3 (Hartig & Buchholz, 2012)：

其中${{\theta }_{pk}}$是随机效应, ${{\theta }_{pk}}\tilde{\ }N\left( 0,\text{ }\!\!\sigma\!\!\text{ }_{{{\theta }_{pk}}}^{2} \right)$, 表示IPE。

此时, IPE可以被视为一个新的维度, 有研究者将它解释为毅力(persistence)或考生努力(examinee effort; Debeer, Buchholz, Hartig, & Janssen, 2014)。此模型假设IPE与被试有关, 即不同位置的题目难度受到被试的影响(Weirich, Hecht, Penk, Roppelt, & Böhme, 2017)。Debeer和Janssen (2013)对上述三类模型进行比较后认为第三类模型更有优势, 即将IPE解释为被试层面的属性更符合实际。

IPE-1假设$\gamma $由题目难度分解得到, 而且不同题目的$\gamma $相同。本质上, $\gamma $是预测变量${{X}_{i0}}$的固定效应：${{X}_{i0}}$对于所有题目都取1, $\gamma $就是所有题目IPE的均值。IPE-2加入的${{\gamma }_{i}}$是基于题目的随机效应, 表示不同题目的IPE可以不同。IPE-3加入的${{\theta }_{pk}}$, 则是基于被试的随机效应, 它表示不同被试的IPE可以不同。其实, 固定效应和随机效应的选择完全基于研究者的需要, 类似于“HLM中设定斜率和截距是固定还是随机”。如果研究者认为IPE具有跨题目一致性, 就可将IPE设定为固定效应; 如果IPE在不同题目上不同, 则可以用一个概率分布(随机效应)来表示IPE。所以在EIRTM中, 设定效应为固定或随机是非常灵活的：通常作为固定效应处理的题目也可以视为随机效应(De Boeck et al., 2011), 这等于带误差项的线性逻辑斯蒂克测验模型(Linear Logistic Test Models, LLTM; Janssen, 2016; Weirich, Hecht, & Böhme, 2014)。

国际大规模测评项目正在经历由纸笔测验(Paper-Based Assessment, PBA)形式向计算机化测验(Computer-Based Assessment, CBA)形式的转变。在国际学生能力评估项目(Programme for International Student Assessment, PISA) 2015的技术报告中(OECD, 2017a)将TME定义为：被试在一种测验模式(如PBA)中的表现与在同一个测验的另一种测验模式(如CBA)中的表现相比, 出现的功能性差异。TME反映的是同一测验在不同测验模式下的结果不可比问题, 它本质上是对测量不变性(measurement invariance)的研究。

为探究TME的实际影响, PISA 2015使用了3个EIRTM模型, 模型1记为TME-1：

其中i代表题目($i=1,2,\cdots ,2I$), 当$i=1,\cdots ,I$时, 表示的是PBA中的题目, 当$i=I+1,I+2,\cdots ,2I$时, 表示的是与前I道题相同的题目, 只是测验形式变成CBA; q表示变量(q = 1,2,L,Q, Q = 2I); ${{M}_{\left\{ i>I \right\}}}$是指示变量, 当$i>I$时${{M}_{\left\{ i>I \right\}}}=1$, 否则取0, 即${{M}_{\left\{ i>I \right\}}}$是不同测验模式的虚拟编码变量; m表示模式, ${{\delta }_{m}}$即TME; $\underset{q=1}{\overset{Q}{\mathop \sum }}\,{{\alpha }_{q}}{{X}_{iq}}={{\alpha }_{i}}$如前文所述, 表示题目区分度; 其余参数含义同上。假设${i}'\in $ $\left\{ I+1,I+2,\cdots ,2I \right\}$, 于是根据模型有${{\beta }_{{{i}'}}}={{\beta }_{{i}'-I}}-{{\delta }_{m}}$, 且假设${{\alpha }_{{i}'-I}}={{\alpha }_{{{i}'}}}$。此模型表示任意PBA中的题目转换为CBA形式后, 题目难度都受到相同的TME (${{\delta }_{m}}$)影响, 但题目区分度不受影响。

第2个模型记为TME-2：

其中${{\delta }_{m}}$变为${{\delta }_{mi}}$, 对于某些题目而言, ${{\delta }_{mi}}$可能为0, 即不同测验模式的难度不变, 不存在TME; 有些题目的${{\delta }_{mi}}$则不为零, 即存在TME。其余参数含义同上。对于前I道题目而言, 因为${{M}_{\left\{ i>I \right\}}}=0$, 所以$\underset{q=1}{\overset{Q}{\mathop \sum }}\,{{\delta }_{mi}}{{M}_{\left\{ i>I \right\}}}{{X}_{iq}}=0$, 于是前I道题目中的题目j的线性成分为${{\eta }_{pjm}}={{\alpha }_{j}}\left( {{\theta }_{p1}}-{{\beta }_{j}} \right)$; 对于后I道题目而言, 因为${{M}_{\left\{ i>I \right\}}}=1$, 所以其中题目j的线性成分为${{\eta }_{pjm}}={{\alpha }_{j}}\left( {{\theta }_{p1}}-{{\beta }_{j}}+{{\delta }_{mj}} \right)$。此模型假设PBA中的题目转换为CBA形式后, 不同题目具有不同的TME。

第3个模型记为TME-3：

其中${{\alpha }_{mi}}$是另一个斜率参数, 称为模式斜率(mode slope), 反映被试的TME在不同题目上的影响不同; ${{\theta }_{p2}}$是另一个潜变量, 表示TME, 为随机效应。假设两个随机效应不相关, 即$\text{cov}\left( {{\theta }_{p1}},{{\theta }_{p2}} \right)=0$。类似地, 对于前I道题目而言, 其中题目j的线性成分为${{\eta }_{pjm}}={{\alpha }_{j}}\left( {{\theta }_{p1}}-{{\beta }_{j}} \right)$; 对于后I道题目而言, 其中题目j的线性成分为${{\eta }_{pjm}}={{\alpha }_{j}}\left( {{\theta }_{p1}}-{{\beta }_{j}} \right)+{{\alpha }_{mj}}{{\theta }_{p2}}$。此模型假设TME是基于被试的效应, 也即不同被试具有不同的TME。

综上, TME-1和TME-2采用基于题目的固定效应(${{\delta }_{m}}$和${{\delta }_{mi}}$)表示TME, 而TME-3则使用基于被试的随机效应(${{\theta }_{p2}}$)表示TME。如果认为${{M}_{\left\{ i>I \right\}}}$是不同测验模式的分组变量, 那么可以更准确地将${{\theta }_{p2}}$定义为被试和模式交互的随机效应。与IPE模型相比, 建构TME模型的思路非常类似：IPE-1和TME-1都加入一个跨题目一致的固定效应; 而IPE-2和TME-2都是从题目的角度出发, 认为效应跨题目不一致性, 只不过IPE-2定义的效应是随机效应, 而TME-2定义的是固定效应; IPE-3和TME-3则都是从被试的角度出发, 认为模型都受到基于被试的随机效应的影响。

PISA采用真实数据对上述三个模型进行比较, 结果发现：TME-3的相对拟合指标最好, TME-2的结果接近TME-3, TME-1的拟合最差; 综合考虑模型的复杂性和数据拟合情况, TME-2的表现最优。基于TME-2的结果还有：绝大多数的题目满足强测量不变性(strong measurement invariance), 即斜率和难度参数在不同测验模式下不变; 部分题目满足弱测量不变性(weak measurement invariance), 即斜率参数不变、难度参数发生变化。可见, CBA的使用确实会对评估学生成绩造成影响(Cosgrove & Cartwright, 2014; Logan, 2015)。值得注意的是, Jerrim (2016)发现中国上海的学生在PISA 2015出现显著的成绩降低, 并且原因很可能就是CBA的使用。无独有偶, 新西兰教育研究委员会(New Zealand Council for Educational Research, NZCER)对PBA和CBA进行比较, 也发现学生成绩出现显著下降(Eyre, Berg, Mazengarb, & Lawes, 2017)。总之, TME的存在已被证实, 考虑TME相比不考虑修正TME能够更好地提升测验质量(Jerrim, Micklewright, Heine, Salzer, & McKeown, 2018)。

DIF是指具有相同能力的被试(组)在作答相同题目时出现的功能性差异, 这种差异是由被试所处群体的不同而造成的。DIF也属于测量不变性问题, 反映的是题目受到与测验无关因素的影响。

用于DIF分析的EIRTM描述如下, 记为DIF-1 (De Boeck et al., 2011)：

其中${{\zeta }_{focal}}$是目标组(focal group)和参照组(reference group)的总效应, 也即两组被试能力均值之差; g表示组, ${{Z}_{g}}$是被试组别的指示变量, 当被试p属于参照组时, ${{Z}_{g}}=0$, 当被试p属于目标组时, ${{Z}_{g}}=1;{{\delta }_{ig}}$即题目i上DIF的效应量, ${{\delta }_{ig}}$本质上是被试组别和题目的交互, 而且${{\delta }_{ig}}$只存在于目标组作答的题目i上, 因为这时${{X}_{iq}}=1$且${{Z}_{g}}=1$; 其余参数含义不变。当被试p属于目标组时, 题目j的线性成分为：${{\eta }_{pi}}={{\theta }_{p1}}-{{\beta }_{j}}+{{\zeta }_{focal}}+{{\delta }_{jg}}$; 当被试p属于参照组时, 题目j的线性成分为：${{\eta }_{pi}}={{\theta }_{p1}}-{{\beta }_{j}}$。

注意此模型同时加入两个固定效应：(1) ${{\zeta }_{focal}}$用于控制目标组和参照组的能力均值差异, 即被试群体间的真实能力差异, Osterlind和Evenson (2009)称之为“影响(impact)”。由于${{\zeta }_{focal}}$基于被试的组别得到, 所以它是基于被试的固定效应。如果有证据支持两组之间没有能力差异或者已经通过匹配等手段进行控制, 则可以移除此效应; (2)$~{{\delta }_{ig}}$是被试组别和题目交互的固定效应, 反映题目难度在组别上的变化。公式(12)假定参照组中所有题目都可能存在DIF (通过指示变量${{X}_{iq}}$定义), 实际上也可以自定义需要估计DIF的题目(如果不需要估计题目j的DIF, 则从$\underset{q=1}{\overset{Q}{\mathop \sum }}\,{{\delta }_{ig}}{{X}_{iq}}{{Z}_{p}}$中移除含${{X}_{ij}}$的项即可)。如何选取需要估计DIF的题目以及是否需要将有DIF嫌疑的题目从匹配标准中排除, 则属于纯化(purification)的问题。

一些研究者基于贝叶斯方法估计DIF-1模型, 因此称之为整合的贝叶斯DIF模型(Integrated Bayesian DIF models, IBDM), IBDM的估计结果优于传统的DIF方法(Gamerman, Gonçalves, & Soares, 2018)。还有研究将此类DIF模型应用于不同的情景和算法中, 侦测出不同组别之间的DIF效应(Bechger & Maris, 2015; Tutz & Berger, 2016; Tutz & Schauberger, 2015)。总之, 虽然此类DIF模型的应用情境有所不同, 但是DIF-1模型最大的优势就是能够自由估计来自不同组别(协变量)的DIF效应。

局部独立性(Local Independence, LI)是IRT理论的基本假设之一, 与LI对立的概念是LD。LD可分为局部被试依赖性(Local Person Dependence, LPD)和局部题目依赖性(Local Item Dependence, LID)。LPD是指在给定被试能力时, 被试在不同题目的作答反应之间存在相依性; LID指题目参数已知时, 不同能力的被试在该题目上的作答反应间存在相依性(詹沛达, 王文中, 王立君, 2013)。

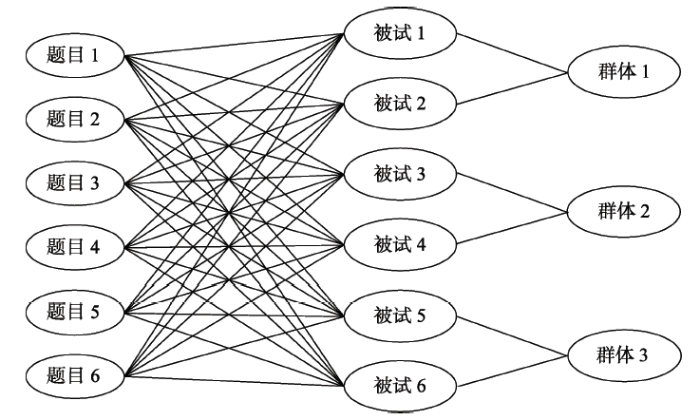
在IRT领域中, LPD出现的主要原因是被试群组效应(Person Clustering Effect, PCE)。选取的被试嵌套于不同的群体, 属于同一群体的被试可能受到相同的外部支持或干扰、具有同样的学习机会和采用相同的解题策略, 因而有理由认为他们的作答相似, 即存在PCE (Jiao, Kamata, Wang, & Jin, 2012)。PCE的存在使得样本量的影响变小, 从而导致有偏的参数估计。为处理PCE导致的LPD, Kamata (2001)提出三水平IRT模型, 对应的层级关系如图1所示。在EIRTM框架下进行重新公式化后, 可以得到LPD-1：

(10 原始公式基于多层广义线性模型(Hierarchical Generalized Linear Model, HGLM), 对GLMM增加限制条件就能得到HGLM (De Boeck & Wilson, 2004)。此处保留了HGLM使用“+”连接被试和题目参数(此时$\underset{q=0}{\overset{Q-1}{\mathop \sum }}\,{{\beta }_{q}}{{X}_{iq}}$解释为题目容易度), 并使用其中一个题目作为参照(故下标从0开始, $Q-1$结束)的习惯。此外, 用${{\varepsilon }_{pg}}$替换了文献中表示PCE的${{\text{ }\!\!\omega\!\!\text{ }}_{00g}}$。这样处理的目的是希望读者能够理解EIRTM框架和HGLM的共性和符号注释上的细微差异。由于HGLM从属于GLMM的框架, 也就是说多水平IRT模型(Multilevel Item Response Theory Model)都可通过EIRTM构建。)

其中$\underset{q=0}{\overset{Q-1}{\mathop \sum }}\,{{\beta }_{q}}{{X}_{iq}}$较之前的表达略有改变, 这表示以某一道题为参照题(一般取最后一题), 得到题目截距β₀, β₁即为题目1与参照题的难度之差, 其余以此类推; 故${{X}_{i0}}$作为题目截距的指示变量, 取值固定为1, 其余$\underset{q=1}{\overset{Q-1}{\mathop \sum }}\,{{X}_{iq}}$含义不变。${{\varepsilon }_{pg}}$表示的是被试p在群体g中的PCE, 为随机效应, ${{\varepsilon }_{pg}}\tilde{\ }N\left( 0,\sigma _{{{\varepsilon }_{pg}}}^{2} \right)$; 其余参数含义不变。于是, 被试p在题目j ($j\ne I$)上的线性成分为：${{\eta }_{pj}}={{\theta }_{p1}}+{{\beta }_{0}}+$ ${{\beta }_{j}}+{{\varepsilon }_{pg}}$ (注意最后一题I上的线性成分为${{\eta }_{pI}}=$ ${{\theta }_{p1}}+{{\beta }_{0}}+{{\varepsilon }_{pg}}$)。此模型表示被试受到所属群体PCE的影响, 而且同一群体中的被试受到的PCE相同。

在IRT领域中, LID出现的主要原因是题组效应(testlet effect, TE)。题组是一组共用相同刺激材料的题目(Wang & Wilson, 2005), 因此被试对同一题组中不同题目的作答不再LI, 而存在TE。忽视TE会对测验信度、被试能力、题目难度、题目区分度参数以及DIF分析造成影响(Bolt, 2002; Ip, 2000; Lee, 2004; Wainer & Lukhele, 1997; Wainer, Sireci, & Thissen, 1991)。包含TE的IRT模型如图2的右侧三列所示, 记为LID-1 (Jiao, Wang, & Kamata, 2005)：

其中$\underset{q=0}{\overset{Q-1}{\mathop \sum }}\,{{\beta }_{q}}{{X}_{iq}}$同式(10); d表示题组($d=1,2,\cdots ,D$); 引入指示变量${{T}_{id}}$, 当题目i属于题组d时, ${{T}_{id}}=1$, 否则${{T}_{id}}=0;{{\gamma }_{pd}}$表示被试p在题组d中的TE, ${{\gamma }_{pd}}$是随机效应, 有${{\gamma }_{pd}}\tilde{\ }N\left( 0,\sigma _{{{\gamma }_{pd}}}^{2} \right);\underset{d=1}{\overset{D}{\mathop \sum }}\,{{\gamma }_{pd}}{{T}_{id}}$可以表示特定题目上的TE; 其余参数含义同上。假设题目j ($j\ne I$)属于题组1, 题目k ($k\ne I$)属于题组2, 对被试p有：$\text{ }\!\!~\!\!\text{ }{{\eta }_{pj}}={{\theta }_{p1}}+{{\beta }_{0}}+{{\beta }_{j}}+{{\gamma }_{p1}},{{\eta }_{pk}}={{\theta }_{p1}}+$ ${{\beta }_{0}}+{{\beta }_{k}}+{{\gamma }_{p2}}$。可见通过使用${{T}_{id}}$, 研究者可以在EIRTM中灵活定义测验的结构：无论是所有题目都基于题组构建, 还是只有部分题目基于题组构建。此模型表示TE是基于被试的随机效应, 即不同被试的TE存在差异。

此外, 造成LID的原因还有可能是不同题目采用相同的测验内容, 即存在内容群组效应(Content Clustering Effect, CCE)。因此, 如图2所示, 题目可以视为既嵌套于题组又嵌套于内容, 即交叉分类(cross-classified)。考虑到此时有两个造成LID的因素, 可称为双重 (dual) LID, 将此模型记为LID-2 (Xie, 2014; Xie & Jiao, 2014)：

其中$\underset{q=0}{\overset{Q-1}{\mathop \sum }}\,{{\beta }_{q}}{{X}_{iq}}$和$\underset{d=1}{\overset{D}{\mathop \sum }}\,{{\gamma }_{pd}}{{T}_{id}}$同式(14); c表示内容($c=1,2,\cdots ,C$); 引入指示变量${{{T}'}_{ic}}$, 当题目i属于内容c, ${{{T}'}_{ic}}=1$, 否则${{{T}'}_{ic}}=0;{{{\gamma }'}_{pc}}$表示被试p在内容c上的CCE, ${{{\gamma }'}_{pc}}$是随机效应, 有${{{\gamma }'}_{pc}}\tilde{\ }N\left( 0,\sigma _{{{{{\gamma }'}}_{pc}}}^{2} \right)$; 其余参数含义不变。同样地, 也可以使用$T_{ic}^{'}$灵活定义测验的内容结构。假设题目j (j≠I)属于题组1且属于内容1, 于是被试p在j (j≠I)上的线性成分为：${{\eta }_{pj}}={{\theta }_{p1}}+{{\beta }_{0}}+{{\beta }_{j}}+{{\gamma }_{p1}}+{{{\gamma }'}_{p1}}$。在此模型中, CCE和TE都是基于被试的随机效应, 不同被试间可以存在差异。

最后, 还可以将LPD和LID相结合, 即在图2右侧的被试上再加入群体, 从而构成最完整的LD模型, 记为LD-1 (Jiao et al., 2015)：

其中的参数含义同上。假设题目j属于题组1且属于内容1, 于是被试p在j (j≠I)上的线性成分为：${{\eta }_{pj}}={{\theta }_{p1}}+{{\beta }_{0}}+{{\beta }_{j}}+{{\gamma }_{p1}}+{{{\gamma }'}_{p1}}+{{\varepsilon }_{pg}}$。${{\varepsilon }_{pg}}$的表示与${{\gamma }_{pd}}$和${{{\gamma }'}_{pc}}$略有不同, 这是因为PCE与TE、CCE不属于同一个水平(层次)：(1) 对于PCE而言, 一个合理的抽样设计不会出现“某些被试属于特定群体, 而另外一些被试不属于任何群体”的情况, 这样本身就会造成被试的异质性; (2) 对于TE和CCE而言, 一个被试可能受到多个TE和CCE的影响, 因此需要通过引入指示变量${{T}_{id}}$和${{{T}'}_{ic}}$来表示某个题目上的作答是否受到TE和CCE的影响以及受到哪个题组或内容的影响。当然, 若整个测验只涉及一个题组和一个内容, 那么LD-1可以简化为：${{\eta }_{pi}}={{\theta }_{p1}}+\underset{q=0}{\overset{Q-1}{\mathop \sum }}\,{{\beta }_{q}}{{X}_{iq}}+{{\gamma }_{pd}}{{T}_{id}}+{{{\gamma }'}_{pc}}{{{T}'}_{ic}}+{{\varepsilon }_{pg}}$。Jiao等人(2015)基于PISA 2006的数据对LPD-1、LID-1、LID-2以及LD-1进行系统的比较, 结果发现：(1) LD-1模型的相对拟合指标最好; (2)在PCE、TE和CCE的影响中, TE影响最大, PCE最小。

综上所述, 上述模型都是基于随机效应处理LD。无论是LPD-1, 还是LID-1、LID-2, 实际上都是通过随机效应处理不同的LD, 这样可以提高IRT模型参数估计的准确性(Koziol, 2016)。实际上, 也可以通过固定效应处理题组造成的LID (参见Hoskens & De Boeck, 1997)。比如, 研究者也可以构建类似3.1和3.2节呈现的三类模型, 以系统地讨论TE的影响。

首先, 这里仅展示基于Rasch模型的EIRTM, 实际上LID模型可以轻易拓展至两参数逻辑斯蒂克(two parameter logistic, 2PL)模型(Fukuhara & Kamata, 2011), 多级记分模型(Jiao & Zhang, 2015), 以及多维模型(Fujimoto, 2018)。其次, 不同测量情境可以自由组合, LD-1是结合LID和LPD而得到。还可以在DIF-1上加入TE或PCE, 此类EIRTM相比传统DIF方法更具有优势(Jin & Kang, 2016; Teker & Dogan, 2015), 甚至可估计题组水平的DIF (Paek & Fukuhara, 2015; Ravand, 2015)。此外, 已有研究基于真实数据进行分析完形填空和阅读理解(Baghaei & Ravand, 2016)。总之, EIRTM的应用非常灵活, 研究者可以基于自身需要与前文提到的IPE、TME、DIF模型相结合, 构建功能更为强大的模型。

此处使用言语攻击数据(Vansteelandt, 2000)对EIRTM的使用进行说明。数据包括316名学生(73名男生和243名女生)在24道题目上的作答。每个题目对应一个情境, 由3个因素决定：情境类型(本人责任, 他人责任)、行为类型(诅咒, 责备, 怒骂)和行为模式(做, 想)。共有$2\times 2\times 3=12$种情境, 每种情境有2道题。具体如表1所示。

将原始的三类作答(“不”、“也许”以及“是”), 转换为0(“不”与“也许”)和1(“是”)评分后, 基于JAGS (Just Another Gibbs Sampler; Plummer, 2017)软件, 采用R 语言“R2jags”包(Su & Yajima, 2015)调用控制, 对此数据进行分析。如需相关代码, 可与作者联系。出于解释的方便, 所有模型基于Rasch模型簇, 主要结果如表2所示。

模型1即为最为基本的Rasch模型, 对应的EIRTM为：

上式中记号的含义与前文一致。以被试p在第1题上的系统成分为例, ${{\eta }_{p1}}={{\theta }_{p}}-\underset{q=1}{\overset{Q}{\mathop \sum }}\,{{\beta }_{q}}{{X}_{1q}}={{\theta }_{p}}-$ ${{\beta }_{1}}={{\theta }_{p}}-\left( -1.162 \right)$, 易知${{\beta }_{q}}$对应各个题目的难度。

模型2类似3.2中的TME, 这里估计的是行为模式效应。注意模型2与TME的测验设计有所不同, 但是模型是等价的。量表的前12道题目是“想”, 后12题是“做”, 这里直接估计出行为模式的效应为-0.465(对应TME-1模型), EIRTM如下：

记号含义与前文一致。被试p在第1题上的系统成分为：${{\eta }_{p1}}={{\theta }_{p}}-{{\beta }_{1}}={{\theta }_{p}}-\left( -1.148 \right)$, 而被试p在第13题上的系统成分为:${{\eta }_{p13}}={{\theta }_{p}}-{{\beta }_{13}}+{{\delta }_{m}}={{\theta }_{p}}-$ $\left( -1.580 \right)+\left( -0.465 \right)$。易知${{\delta }_{m}}$对应不同模式造成的效应。

模型3对应3.3中的DIF模型, 出于说明的方便, 这里没有讨论男女组能力均值不同的情况, 对应的EIRTM公式如下：

这里将女性作为参照组(${{Z}_{g}}=0$), 男性作为目标组(${{Z}_{g}}=1$)。所以女生p在题目1上的系统成分为：${{\eta }_{p1}}={{\theta }_{p}}-{{\beta }_{1}}={{\theta }_{p}}-\left( -1.196 \right)$, 男性m在题目1上的系统成分为：${{\eta }_{m1}}={{\theta }_{m}}-{{\beta }_{1}}={{\theta }_{m}}-\left( -1.196 \right)+$ $\left( -0.101 \right)$。${{\delta }_{ig}}$对应题目的DIF效应量, 结合提供的95%的置信区间, 就可以直接判断${{\delta }_{ig}}$是否显著。此处, 第6、14、16、17、19、20题的DIF效应显著。

模型4考虑的是3.4中提到的CCE, 对应的EIRTM如下：

由表4易知量表的内容(题干)能够归为4类, 对应4个随机效应${{{\gamma }'}_{pc}}$。不同被试在不同内容上的${{{\gamma }'}_{pc}}$都不同, 以第1个内容为例, ${{{\gamma }'}_{p1}}\tilde{\ }N\left( 0.004,0.442 \right)$。当具体到被试1在题目1上的作答时, JAGS可以估计出${{{\gamma }'}_{11}}$的值为-0.398, 系统成分为: ${{\eta }_{11}}={{\theta }_{1}}-{{\beta }_{1}}+{{{\gamma }'}_{11}}={{\theta }_{1}}-\left( -1.248 \right)+\left( -0.398 \right)$; 被试1在题目2上作答时, 由于属于同一个内容, 系统成分为: ${{\eta }_{12}}={{\theta }_{1}}-{{\beta }_{2}}+{{{\gamma }'}_{11}}={{\theta }_{1}}-\left( -0.584 \right)+\left( -0.398 \right)$。

最后, 值得一提的是JAGS采用的是贝叶斯方法, 可以通过离差信息指数(Deviance Information Criterion, DIC)来评估模型的整体拟合情况, DIC越小说明模型的预测能力越好。这4个模型中, 模型3的DIC最小(DIC = 7855.3), 即拟合最好。

本文的第3部分详细介绍了如何使用EIRTM检测IPE、TME以及DIF, 这些都反映EIRTM能够方便地处理测量不变性问题：IPE是题目位置对测量不变性的影响, TME是测验形式对测量不变性的影响, DIF是受测群体对测量不变性的影响。通过EIRTM处理测量不变性问题可以解决传统IRT方法(即“两步法”)的困境：如果测量不变性不满足, 那么IRT得到的参数估计本身就是有偏的; 基于有偏的参数估计, 并不能得到可信的结果。因此即使基于“两步法”证明数据满足测量不变性, 也有可能是不准确的参数估计造成的。

此外, EIRTM可以构建全面的测量不变性模型, 得到尽可能准确的参数估计结果。读者可能已经意识到, 鉴于EIRTM的灵活性, 可以将第3部分中提到的模型进行整合, 得到一个既能估计IPE、TME和DIF, 又考虑LD的模型。换言之, 只要符合研究实际, 研究者可以一步到位, 同时处理多个测量问题。

最后, EIRTM可以将测量不变性问题与解释性分析相结合, 也即在估计IPE、TME或DIF的同时, 也考虑被试和题目特征的影响。此类模型能够通过控制测量不变性的相关效应, 得到更为准确的被试和题目效应; 反之亦然。实际上, DIF-1就是在控制组别的固定效应后, 再估计DIF效应。

EIRTM提供一个统一而灵活的IRT模型框架, 并且越来越受到研究者重视。受限于篇幅和主旨, 本文没法更全面地展示EIRTM与现有IRT模型的转换关系, 除本文涉及的模型外, 使用EIRTM还可以建构多级记分的IRT模型和多维IRT模型、动态Rasch模型(Dynamic Rasch Models)、纵向IRT模型以及含反应时的IRT模型等等(参见De Boeck & Wilson, 2004; Klein Entink, Kuhn, Hornke, & Fox, 2009; Rijmen et al., 2003; Wilson, Zheng, & McGuire, 2012)。以EIRTM为代表的广义建模方法(Generalized Modeling Approaches)具有诸多优越性, 目前已经得到业内研究者的重视。在新编著的《项目反应理论手册(第一卷)：模型》(Handbook of Item Response Theory, Volume One: Models; van der Linden, 2016)的最后一部分, 专门介绍了4种广义建模方法, 这值得国内研究者重视。

此外, EIRTM还体现了IRT模型和回归模型的共性。传统的心理和教育测量领域中, 很少有研究者注意到回归模型、GLM、HLM和IRT模型之间的联系：在回归模型的基础上, 加入随机效应, 可以推广至HLM; 引入连接函数, 可以得到GLM; 同时加入随机效应和连接函数, 可以得到EIRTM。这一综合的分析框架, 不仅有助于研究者深入认识以IRT为代表的现代测量理论与经典回归分析的联系, 也有利于相应的教学和实践活动。

EIRTM具有广阔的应用前景, 可以广泛应用于心理和教育测量领域中。除了上文所述的通过EIRTM建构合理的测量模型以外, EIRTM还可用于分析复杂表现任务(complex performance task)。对于复杂表现任务进行评价, 是教育与心理测量领域面临的新挑战(Mislevy, 2016)。比如, PISA 2015就使用合作问题解决任务, 以展示学生在动态、交互情景中的表现(OECD, 2017b)。EIRTM以其灵活的框架为评价复杂表现任务提供了一种解决思路, 通过EIRTM可以将涉及的任务属性的特征纳入模型, 从而得到被试能力的准确估计。

当然EIRTM也存在一些问题：(1) 算法比较复杂, 运算时间相对较长。对于蒙特卡洛(Monte Carlo)模拟研究以及自适应测验而言, 只能尝试通过提高计算机的计算性能来改进效率。但是对于不需要重复的应用研究来说, 现有软件的运行速度基本可以接受; (2) EIRTM的使用对数学能力和编程能力要求较高, 这不太利于一般研究者的使用。EIRTM涉及的算法比较复杂, 非统计学/数学专业的研究者不容易理解; 而且目前没有简单易用的专用软件可供使用, 必须由研究者自己编写程序, 并设定模型参数。总之, 尽管EIRTM也存在一些不足, 但是考虑到EIRTM的重要理论意义与应用价值, 未来必定能在测量领域大有作为。