1 引言
基于经典概率理论的传统决策模型已经在决策领域取得了很大的成功, 但却不能很好地解释人在不确定或矛盾状态下的决策行为。近10年来, 一种基于量子理论的量子决策模型能够解决传统概率模型难以解释的决策问题。这一新决策模型的出现, 打破了传统决策模型中经典概率理论的禁锢, 为决策理论的发展带来了新的方向。
长期以来, 心理学家就人类决策问题提出了两种决策理论, 传统即古典决策理论和启发式决策理论(Baron, 1988; Gilboa, 2009)。古典决策理论认为个体具备完全的理性能力, 总是追求个人利益的最大化。在数学层面上, 遵循理性决策的个体根据贝叶斯定理做出推断, 并根据期望定理做出决定(Chater, Tenenbaum, & Yuille, 2006; Tenenbaum, Griffiths, & Kemp, 2006)。启发式决策理论指出, 人在不确定条件下进行的决策并非总是理性的, 更多会根据几种启发式方法进行判断和决策, 如代表性启发法、易得性启发法与锚定和调整启发法(Tversky & Kahneman, 1974)。
量子理论是20世纪人类最伟大的成就之一, 它提供了新的有关自然界的观察、思考和表述方法, 尤其是它所蕴含的开放性和不确定性, 启发人类更多的发现和创造。量子决策模型正是受此影响而建立, 该模型与启发式理论相似, 认为人的决策是有限理性的(bounded rationality), 但量子决策模型也与古典决策理论一样, 有严密而完备的数学逻辑体系。但相比于古典决策理论, 该模型具有更加新颖与灵活的理论结构(Aerts, Sozzo, & Veloz, 2016; 孙炯, 王万义, 赫建文, 2010)。
当然, 借鉴一种来源于物理学的理论来解释人的决策过程, 在吸引眼球的同时自然会引起争议——为什么量子理论可以用于解释人的决策过程?量子概率理论与经典概率理论有何异同?量子决策模型有哪些实证性的证据?接下来, 本文将从这三个方面对量子决策模型进行讲解。
2 使用量子决策的原因
2.1 决策中的不确定状态
大多数传统决策模型(如贝叶斯网络模型或产生式模型)认为, 虽然在不确定状态下, 个体决策的信念状态(belief state)会随时间变化, 但是某一特定时刻的信念状态会处于某一确定状态(Asano, Basieva, Khrennikov, Ohya, & Tanaka, 2012)。虽然这些决策模型在决策领域已经取得了很大成功, 但是这类传统的决策模型也存在缺陷:从实际来说, 人在决策中的信念状态是未知的, 是由研究者假定的, 因而不能简单地认为人在决策过程中处于确定的信念状态(Busemeyer & Bruza, 2012)。
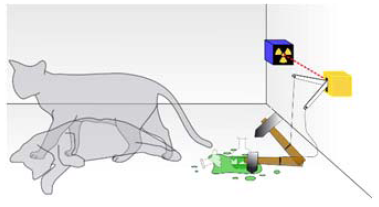
量子决策模型对人在决策过程中所处的不确定信念状态有很好的描述。这种描述可以通过一个著名的例子——“薛定谔的猫”来进行诠释(图1)。所谓薛定谔的猫是指:将一只猫关在一个箱子里, 箱子中放了一个盖革计数器、一块放射性物质、一把小锤子以及一只装着毒药的氢氰酸小瓶, 假定放射性物质发生衰变的可能性为50%。当衰变未发生时, 装毒药的小瓶是封口的, 完好无损, 猫活着。当发生衰变时, 继电器操纵小锤子, 击碎装有毒药的小瓶, 猫被毒死(苏汝铿, 2002)。这里, 薛定谔提出了一个问题:在未打开箱子观察猫之前, 这只猫的状态是什么?是死还是活?以传统的观点来看, 这只猫不是死的就是活的, 处于确定状态。而量子理论认为, 这只猫所处的状态是一种不死不活, 既死又活的状态, 科学家将这种混沌的状态称为叠加态(曾谨言, 2014)。
图1
叠加态是指在这一状态下, 一切潜在的确定状态都有发生的可能, 这种叠加状态就是所有冲突、模糊与不确定因素的固有体现。因此, 量子理论对决策中决策者不确定的信念状态的描述与解释具有得天独厚的理论优势(De Barros & Suppes, 2009; Busemeyer & Bruza, 2012)。
2.2 测量对决策的影响
心理学研究者大多通过被试的主观报告来记录其在决策时所处的心理状态, 并认为所测量的结果能够准确代表被试做出反应那一时刻所处的认知状态。例如, 被试在观看一部惊悚电影时被问到是否感到害怕, 被试的回答就反映了其回答问题前的心理状态(害怕或是不害怕)。
量子理论认为, 测量时, 所测的结果并不能准确反映测量前事物的性质, 测量可以改变所测事物的性质(顾樵, 2014)。试想, 通过一个特定问题(相当于一种对认知状态的测量)所测得的状态往往是确定的, 这与测量前这个人所处的不确定状态不符。还以上例来说, 在观看电影时, 被试的情感状态可能是模糊不清的(可能是害怕, 也可能是激动等等, 为一种叠加态), 但当被试回答感到害怕时, 表示所测量得到的结果是一个确定的状态, 这种确定的状态并不能完全反映被试模糊不清的感情。从更深层的角度上来说, 测量所得的确定的认知状态其实是该测量问题与原先的那种不确定状态共同作用的结果(Blutner, Pothos, & Bruza, 2013)。
2.3 顺序效应与不确定性
量子决策理论指出, 若一个人处于不确定状态, 那么一个问题的提出(即一种测量)可以使其转变为一个确定状态, 不同问题对应的转变状态往往是不同的, 对接下来提出的其他问题的回答也是不同的。也就是说, 先提出的问题会影响被试对后续问题的回答, 这也就是决策中的顺序效应。传统决策模型, 由于其依赖于经典的概率理论在解释这类顺序效应时往往会出现困难, 例如, 在一项1997年美国总统候选人的民意调查中, 调查者发现当两个问题呈现的顺序变化时, 人们回答的结果也发生了显著的变化(Moore, 2002), 这违反了经典概率中的相容性原则(关于相容性详见本文2.4节)。虽然传统决策模型会借助于一些约束性的假定(如贝叶斯干涉模型) (Busemeyer & Bruza, 2012)来解释这种顺序效应, 但是这些约束性的假定不仅降低了模型的灵活性, 而且使得整个模型变得繁琐。
在量子理论中, “不确定性原理”指当我们测量一个微观粒子时, 不可能同时确定它的位置和动量, 这种原理蕴涵于量子理论的数学结构中(苏汝铿, 2002)。在心理学领域, 一个人对于两个不同事件的理解或看法, 往往也是“不能同时确定”的:当决策过程中的一个问题创造了一个确定的状态后, 另一个问题的出现会动摇这一状态的确定性。例如, 一个人计划买一辆车, 奥迪或大众, 如果只问这个人自己的喜好, 那么他肯定会选择奥迪; 但是, 若先问他妻子的喜好(大众), 随后再问他自己的喜好, 他就可能不会那么肯定地选择奥迪。在这个例子中, 当他从他妻子的角度做出喜好判断时, 他自己的喜好就变得不确定了。即, 当研究者对被试的某一种状态进行准确测量时, 就无法准确获知他此时其它的状态。
2.4 人的判断并不总是服从经典逻辑
大多数传统决策模型建立在经典概率理论的基础之上, 经典概率模型中的逻辑关系称为布尔逻辑。在布尔逻辑中, 有一条称为全概率法则的定理(the law of total probability), 通过这一定理可以推导出决策领域中著名的贝叶斯定理(罗俊明, 2002)。但是, 一些心理学研究发现, 在分离(disjunction)实验和分类-决策(category-decision making)实验中, 实验所得的结果常常违背全概率法则(Lewinski, 2015; Pothos & Busemeyer, 2009; Wang & Busemeyer, 2016)。
量子逻辑, 由著名数学家冯·诺依曼(Von Neumann)提出, 他将事件定义为在希尔伯特空间中的一个个子空间, 这样便使得量子概率不需要受到诸如全概率法则等诸多布尔逻辑法则的约束(Bruza, Wang, & Busemeyer, 2015)。因此, 量子决策理论能够允许那些违背全概率法则的事件存在。Busemeyer和Bruza (2012)指出, 量子逻辑其实是一种泛化的布尔逻辑, 它没有布尔逻辑中许多约束式限定, 具有更大的灵活性与随机性, 更有利于解释人的判断和决策。
3 量子概率理论和经典概率理论的比较
量子概率理论和经典概率理论分别是量子决策和古典决策模型的数学基础, 这两种概率理论之间的区别决定了量子决策模型和传统决策模型的区别。因此, 本节简要对比并分析这两种概率理论的异同之处。
3.1 空间与事件的定义
经典概率理论定义样本空间Ω, 表示所有可能发生事件的集合。事件可能出现的所有结果都以样本点的形式存在于样本空间。实验中可能发生的每个事件都是样本空间的子集, 若A为一个事件, 则A$\subset$Ω, 同理若B也为一个事件, 则也有B$\subset$Ω; 并且此时两事件的并事件A∪B以及交事件A∩B也是样本空间中可能发生的两个事件。
量子概率理论存在于希尔伯特空间中, 若该空间由N个彼此正交的单位向量V$\{V=\left| V \right\rangle ,$ i=1,…,N}所决定, 那么则称该空间为N维的希尔伯特空间, 这N个向量称为此空间的基矢。事件A对应于希尔伯特空间的一个子空间, 由基矢VA$\subset$V所决定, 该事件同时也对应一个投射算符(密度矩阵)PA =$\sum\limits _{i\in A}\left| {{V}_{i}} \right\rangle \left\langle {{V}_{i}} \right|$(Aerts, 2009)。若事件A, B为存在于希尔伯特空间的两个事件, 则称空间VA+VB为两事件的并事件空间, 交空间VA∩VB为两事件的交事件空间(Aerts & Gabora, 2005; 史荣昌, 魏丰, 2010)。
3.2 概率的定义
经典概率理论认为, 概率是将样本空间中每个事件A与通过一个映射p与实数p (A)建立的一种对应的关系, 其中p (A)值域为[0,1]。若A, B为相互排斥的两个事件, 即A∩B=ø, 那么则有p (A∪B)= p (A)+ p (B)。
量子概率理论首先定义希尔伯特空间中任意一单位向量S为初始状态, 在这一状态下发生事件A的概率可以看作向量S可被A的基矢VA$\subset$V描述的程度, 其数学表达式为p (A) =${{\left\| {{\mathbf{P}}_{\mathbf{A}}}\left| S \right\rangle \right\|}^{2}}$, 若A, B为互斥事件, VA∩VB = ø, 即PA.PB = 0那么此时并事件的概率p (A∪B) = $\text{ }\!\!~\!\!\text{ }{{\left\| ({{\mathbf{P}}_{\mathbf{A}}}+{{\mathbf{P}}_{\mathbf{B}}})\left| S \right\rangle \right\|}^{2}}$ = ${{\left\| {{\mathbf{P}}_{\mathbf{A}}}\left| S \right\rangle \right\|}^{2}}$+ = p (A)+ p (B)。
3.3 条件概率
在经典概率理论中, 若事件A, B为样本空间中两个事件, 那么在事件A已经发生的条件下, 发生事件B的条件概率p (B|A)= p (A∩B)/p(A)。若样本空间存在一个划分Xk{k=1,…,N}, 那么则有∑p (Xk | A) = 1, 在条件A的状态下, 可将分母p (A)看为归一化因子, 用以保证在此状态下全空间概率总和为1。
量子概率理论认为, 当事件A发生后, 此时人的状态将从原状态$\left| S \right\rangle $转变为$\left| {{S}_{A}} \right\rangle ={{\mathbf{P}}_{\mathbf{A}}}\left| S \right\rangle /$ $\left\| {{\mathbf{P}}_{\mathbf{A}}}\left| S \right\rangle \right\|$。与经典概率类似, 分母$\left\| {{\mathbf{P}}_{\mathbf{A}}}\left| S \right\rangle \right\|$可视为归一化因子, 保证新状态$\left| {{S}_{A}} \right\rangle $的模长为1, 即保证状态的完整性。
3.4 相容性
相容性是指两个事件A, B可以同时发生, 或是两个事件之间不存在顺序效应(苏汝铿, 2002)。经典概率理论认为在任一给定的实验中, 只存在一个样本空间, 其中包含实验中可能发生的所有事件。在这样的定义下, 任意两事件的并或交事件也是明确的。并且由条件概率可知, p (A∩B) = p (A) p (B|A) = p (B)p (A|B)=p (B∩A), 表明在经典样本空间中, 事件A, B的发生顺序并不影响复合事件AB的概率, 即在经典概率理论中, 事件总是相容的, 不会出现顺序效应。
在量子概率理论中, 事件所存在的希尔伯特空间是由一组正交归一的基矢所决定的, 但这组基矢不是唯一的, 从理论上来说是可能存在无穷多组的。当两个事件A(VA$\subset$V)和B(WB$\subset$W)由不同的基矢组所决定时, 这两个事件的交或者并事件就不再明确了。并且运用数学推导可知, 此时事件AB发生的概率为p (AB) =${{\left\| {{\mathbf{P}}_{\mathbf{B}}}{{\mathbf{P}}_{\mathbf{A}}}\left| S \right\rangle \right\|}^{2}}$, 而BA发生的概率p(BA)=$\text{ }\!\!~\!\!\text{ }{{\left\| {{\mathbf{P}}_{\mathbf{A}}}{{\mathbf{P}}_{\mathbf{B}}}\left| S \right\rangle \right\|}^{2}}$。注意到式中PA和PB表示两个不同的矩阵, 而矩阵乘法不满足交换律即PA.PB ≠ PB.PA, 故此时p (AB) ≠ p (BA), 说明事件存在不相容性。
总之, 在一些特定的情况下(如两事件互斥), 量子概率理论和经典概率理论具有相同的表述形式; 除此之外, 两者之间存在明显的差异。其中, 量子概率理论中蕴含的不相容性是其与经典概率理论的主要区别(Busemeyer & Wang, 2015; Busemeyer, Wang, Khrennikov, & Basieva, 2014), 而在现实决策中, 测量问题间不相容所体现的顺序效应往往也是存在的, 是能够通过量子决策模型解释的, 这也从另一方面印证了量子概率理论的优越性。
4 量子决策模型在研究中的应用
4.1 分离效应
分离效应(Disjunction Effect)是由Tversky和Shafir在1992年探究确定事件原则(sure thing principle)理论的过程中提出的(Tversky & Shafir, 1992)。确定事件原则是标准决策理论的一条基本原则, 它隐含着理性人的假设, Savage (1954)把这一原则描述为, 如果决策者知道事件E会发生, 他会采取行动A; 如果决策者知道事件E不会发生, 他仍会采取行动A; 以此观之, 决策者在不知道事件E是否会发生的情况下, 都会采取行动A。然而许多研究表明, 决策者并非总是遵循这一原则。Tversky和Shafir (1992)在实验中, 让被试假想自己刚刚玩了一个50%的可能赢得$200, 50%可能输$100的游戏。发现在知道自己赢了的情况下, 较多人(69%的被试)选择再玩一次同样的游戏; 在知道自己输了的情况下, 较多人(59%的被试)也选择了再玩一次; 然而, 在不知道是赢还是输的情况下, 较少人选择再玩一次(只有36%的被试, 而按照经典概率理论应在69%和59%之间)。Tversky和Shafir把这一怪异的现象称为分离效应(汪祚军, 李纾, 2008)。并分别提出了基于理由(reason-based decision making)的假设和思维惰性(reluctance-to-think)假设来解释这一现象, Li, Jiang, Dunn和Wang (2012)基于这两种假设对分离效应进行了研究, 并进一步指出仅存在不确定状态不足以产生分离效应, 对两种确定状态选择理由的差别是导致分离效应产生的必须条件。2002年, Li和Taplin提出了齐当别(equate-to- differentiate model)理论, 很好地解释了在一次性2人囚徒困境博弈中检测到分离效应(Li & Taplin, 2002)。Bagassi和Macchi (2006)认为分离效应的产生是由在描述决策过程中人为地掺入无关目的造成的, Sun, Li和Li (2008)对分离效应产生的研究, 验证了Bagassi和Macchi对分离效应产生原因的解释。此外, Wang, Li和Jiang (2012)进行了有关分离效应的情绪研究, 发现在不确定情况下人们会产生更消极的情绪反应。
从量子理论的观点来看, 这一心理学现象类似于量子力学中著名的双缝衍射。图2为双缝衍射实验的简图, P代表一个光子, 它可以穿越两个狭缝(S1和S2)最终到达D1或D2所示的位置。在一种观测条件下, 研究者不仅观察光子最终到达的位置(D1或D2), 还要观察其穿过的通道(S1或S2), 研究显示:当光子经过通道S1时, 其最终到达D1和D2的概率相等, 都为50%; 当光子经过S2时, 会出现相同的结果。在另一种观测条件下, 研究者只观测光子最终到达的位置, 而不观测其路径, 实验结果却十分奇怪:光子到达D1的几率明显小于D2。
图2
可以看出, 上述衍射实验与赌博游戏实验有许多相似之处(Busemeyer, Wang, & Townsend, 2006)。首先, 实验都包含两条明确地路径:对于分离实验来说, 两条路径分别对应的是第一局游戏输或赢两种结果; 而双缝实验则对应S1和S2两个狭缝。其次, 在实验中, 光子的运行路径和参与者的决策过程都分为确定(观测)和未知(不观测)两种情况。最后, 在未知路径(未知输赢)的情况下, D1(做出继续游戏决定)概率都会发生显著的下降。量子理论认为, 在不进行观测, 也就是未知输赢的情况下, 参与者和光子都处于上文所述的叠加态, 而不是确定的状态(S1或S2, 输或赢), 这种状态与随后的测量产生了干涉, 导致了决策者做出继续游戏/光子到达D2的概率降低, 具体的数学推导会在下一例中给出。
4.2 分类-决策中的干涉效应
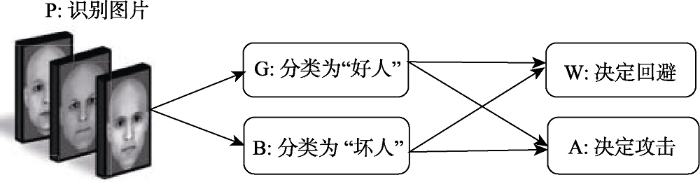
分类-决策(Categorization-decision)实验范式是由Townsend, Smith, Wenger和Silva (2000)年提出的, 随后Busemeyer, Wang和Lambert-Mogiliansky (2009)在该实验范式的基础上对建构了量子决策模型。该实验流程为, 通过电脑向被试展示一些人脸图片(分为好人和坏人两种)。在一种情况下(C-then-D), 被试需要先将这些“人脸”分为好人和坏人两类, 然后再决定采取攻击或是回避行为; 在另一种情况下(D-alone), 被试只需决定攻击或是回避即可。当被试对“坏人的脸”进行攻击或是对“好人的脸”采取回避时, 会有70%的概率获得奖励, 反之则会有70%的概率接受惩罚(Wang & Busemeyer, 2016)。该实验的部分实验结果如表1所示。
表1 分类-决策实验的部分实验结果(资料来源:Busemeyer & Bruza, 2012)
| C-then-D | D-alone | ||||
|---|---|---|---|---|---|
| p (G) | p (A|G) | p (B) | p (A|B) | pT(A) | p (A) |
| 0.17 | 0.41 | 0.83 | 0.63 | 0.59 | 0.69 |
表1中, p (G)和p (B)分别对应将人脸分类为好人和坏人的概率, p (A|G)和p (A|B)分别表示在分类为好人和坏人的情况下采取攻击决定的概率。可以看出, 在分类为坏人的情况下, 采取攻击的概率p (A|B)要大于分类为好人的情况下采取攻击的概率p (A|G), 这符合常规的逻辑。根据经典理论中的全概率原则, p (A)应服从式(1)的全概率定理:
p (A) = pT(A) = p (G) p (A|G) + p (B) p (A|B) (1)
图3
量子理论认为, 状态转变的概率振幅(probability amplitude)可通过两个状态的内积来定义(Busemeyer et al., 2014), 例如状态P→G的转变(从初始状态P向分类为好人状态G的转变)可通过狄拉克符号$\left\langle G\text{ }\!\!|\!\!\text{ }P \right\rangle $来表示, 同理, 在分类为好人的情况下做出攻击决定的概率振幅, 也就是状态G→A的转变概率振幅, 可表示为$\left\langle A\text{ }\!\!|\!\!\text{ }G \right\rangle $。需要注意的是, 该符号代表的数是复数而不是实数, 这是其称之为“振幅”的原因, 而其对应的实数概率(经典概率), 大小与其模的平方相等, 即上述发生两个过程的概率可分别写作${{\left| \left\langle G\text{ }\!\!|\!\!\text{ }P \right\rangle \right|}^{2}}$和${{\left| \left\langle A\text{ }\!\!|\!\!\text{ }G \right\rangle \right|}^{2}}$, 这种简单过程的概率数值与经典概率中的p (G)和p (A|G)相等。在C-then-D情况下, P→G→A的概率, 也就是将图片分类为好人后作出攻击决定的概率, 可以写成$\left| \left\langle A\text{ }\!\!|\!\!\text{ }G \right\rangle \right|.{{\left| \left\langle G\text{ }\!\!|\!\!\text{ }P \right\rangle \right|}^{2}}$, 在这种情况下, 其大小与p (G)和p (A|G)的乘积相等, 同理, 将图片分类为坏人后进行攻击的概率, 也就是P→B→A的概率, 可写作${{\left| \left\langle A\text{ }\!\!|\!\!\text{ }B \right\rangle .\left\langle B\text{ }\!\!|\!\!\text{ }P \right\rangle \right|}^{2}}$, 其大小与p (B)和p (A|B)的乘积相等。不难看出, 在这种清晰路径的决策过程中, 量子理论与经典理论的结论是一致的。而在D-alone情况下, 从P→A的概率可以仿照全概率公式的形式写为如下的形式, 需要注意的是, 虽然形式上接近, 但这两个式子是有本质上的区别。为了更方便的进行对比, 我们可以对式中$\left\langle A\text{ }\!\!|\!\!\text{ }G \right\rangle .\left\langle G\text{ }\!\!|\!\!\text{ }P \right\rangle $和$\left\langle A\text{ }\!\!|\!\!\text{ }B \right\rangle .\left\langle B\text{ }\!\!|\!\!\text{ }P \right\rangle $做出欧拉变换, 令其等于$\sqrt{p\left( G \right)p\left( A\left| G \right. \right)}.{{e}^{i\alpha }}$和$\sqrt{p\left( B \right)p\left( A\left| B \right. \right)}.{{e}^{i\beta }}$, 其中α和β称为相位角(李红, 谢松法, 2013), 是表征不同决策路径的参数。
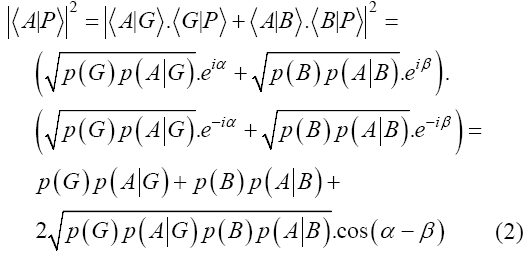
可以看出, 相比于经典概率理论(式(1)), 上式(2)多出了最后一项(干涉项) $2\sqrt{p\left( G \right)p\left( A\left| G \right. \right)p\left( B \right)p\left( A\left| B \right. \right)}.$ $~\text{cos}\left( \alpha -\beta \right)$, 这便是两个概率振幅产生的干涉项(即决策者在选择潜在的决策路径过程中产生的干涉)。若我们令cos (α-β) = 0.33, 那么我们便可得出${{\left| \left\langle A\text{ }\!\!|\!\!\text{ }P \right\rangle \right|}^{2}}$为0.69, 这便与实验得出的p (A)的结果符合, 这种干涉效应便得以解释1(1在这类问题中, α和β相当于确定一个“参照系”且其取值并非唯一确定的, 解释问题的关键在于相位角的差值α-β。)。
4.3 合取谬误
合取谬误(conjunction fallacy)是指复合事件中组成部分发生的概率要小于复合事件发生的概率。典型的合取谬误的例子便是Tversky和Kahneman做出的关于著名的Linda问题的研究(Artemenkov, 2006; 刘程浩, 徐富明, 王伟, 李燕, 史燕伟, 2015)。在该研究中首先呈现给被试关于一个叫做Linda的人物特征及活动情况的描述如下:“Linda是一位31岁的单身女性, 直率并且非常聪明。在大学期间, 她主修哲学, 对种族歧视问题和社会偏见非常关注, 同时也参加过反核示威游行。”然后要求被试对包括以下事件在内的8个关于人物Linda的事件进行概率判断:(1) Linda是一名银行出纳员(T); (2) Linda是一名女权主义者和银行出纳员(F∩T)。按照经典概率理论, 被试做出第二种情况判断的概率p (F∩T)要小于第一种情况p (T), 但实际结果却恰恰相反。
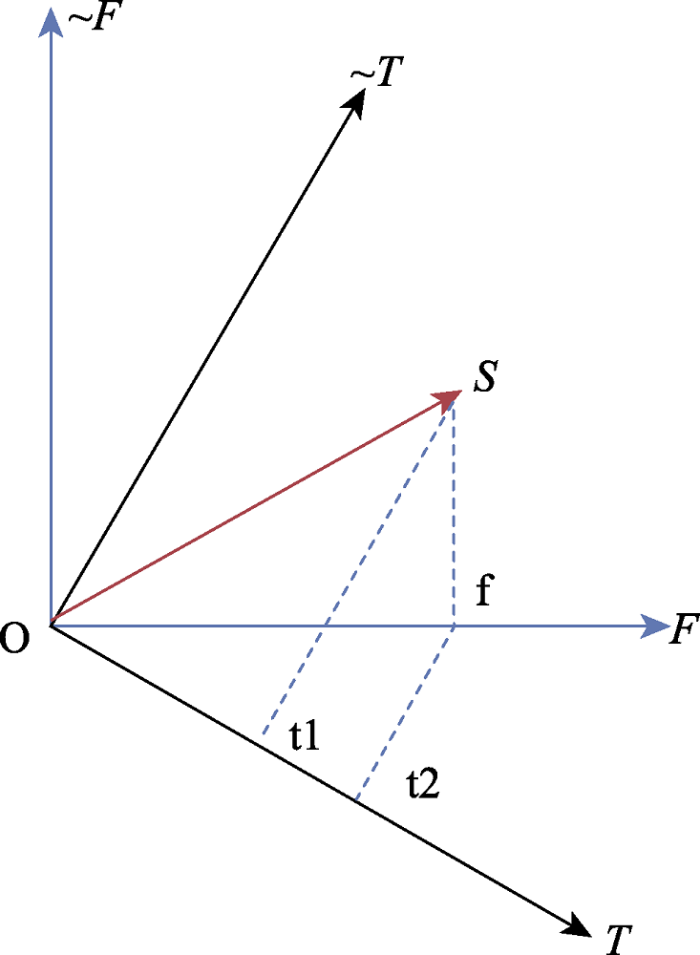
量子决策理论可通过几何式的投射定理来解释这种违反经典决策理论的现象, 即图4所示简易的两维模型。两组正交直角坐标系分别表示两个不同问题的信念状态:F轴表示认同Linda是女权主义者, ~F轴表示不认同Linda是女权主义者; T轴表示认同Linda是一名银行出纳员, ~T轴表示不认同Linda是银行出纳员(Busemeyer & Wang, 2015)。被试最初的观点通过单位向量S来表示。被试认为Linda为女权主义者的概率幅$\left\langle F|S \right\rangle$等于S投影在F轴上的长度, 故其概率为该投影长度的平方; 同理, 被试判断Linda为银行出纳员的概率等于S投影于T轴上的长度的平方。注意到在研究中对于Linda的描述更能使人感觉Linda是一名女权主义者, 因此, 图中的被试在做出判断前的初始状态S更靠近F轴。根据量子理论, 当被试先做出Linda为女权主义者的判断时, 其信念状态也随之从S转变为F, 被试随后做出银行出纳员的判断时, 其信念状态从F转变为T, 而这一复合事件的概率幅就等于S投影至F, 再从F投影至T的长度, 即线段Ot2。可以看出, 该线段的长度大于从S投影至T的线段长度Ot1, 说明被试做出判断(2)的概率要大于判断(1)。
图4
需要指出的是, 几何投影法和上例中的代数法本质相同, 几何投影法相比于代数推导法, 更加直观明了。但这种几何投影法只能运用于问题状态是二维或者三维简单情况(即简单欧几里德空间中的问题), 故而在涉及复杂问题时一般不会使用几何投影法。例如, 分析Shafir和Tversky (1992)、Li和Taplan (2002)与Busemeyer等人(2006)囚徒困境博弈研究中出现的分离效应时, 需要在四维希尔伯特空间中建构决策模型。在此空间中定义被试初始信念与行为的状态${{\psi }_{0}}$, 并根据博弈中的收益矩阵(pay-off matrix)来确定哈密顿矩阵HA (指在薛定谔方程中出现的一类特殊矩阵), 该矩阵在特定收益条件下推动被试状态空间的转变。且该理论引入另一类哈密顿矩阵HB, 以表征被试在决策过程中的认知失调。最后将上述三者代入薛定谔方程${{\psi }_{t}}={{e}^{-it\left( {{\mathbf{H}}_{\mathbf{A}}}+{{\mathbf{H}}_{\mathbf{B}}} \right)}}.{{\psi }_{0}},{{\psi }_{t}}$表示被试决策过程中动态变化的信念与行为状态, 并依此解释其中出现的分离效应(Pothos & Busemeyer, 2009)。
4.4 量子问题等式
由Wang和Busemeyer (2013)提出的量子问题等式(quantum question equality), 是一种对于顺序效应的先验性预测模型。这一模型可以精确地量化预测顺序效应大小, 证明量子决策模型不仅仅是一种后验性的模型(Yearsley & Busemeyer, 2016)。在实验中, 被试会被问到两个问题(假设为A和B), 并以不同顺序出现(AB或是BA)。p (Ay, Bn)表示被试对问题A肯定回答后对问题B的回答为否定的概率, 同理p (Bn, Ay)表示被试对B问题作出否定回答后再对A作出肯定回答的概率, 同理p (An, By)和p (An, By)的定义也类似。运用量子理论构建的量子问题等式为:[p (Ay, Bn)-p (Bn, Ay)]= -[p (An, By)-p (By, An)]。
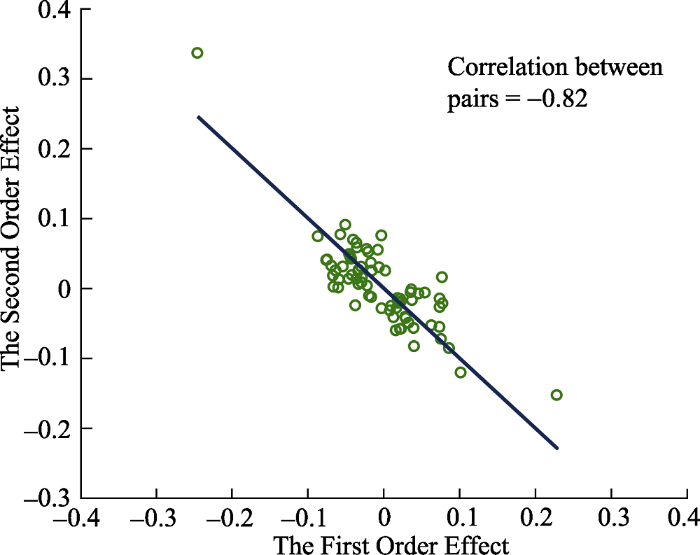
Busemeyer和Wang (2015)在70个不同地区中使用不同的问题进行了实验, 其实验结果如图5所示。横坐标表示p (Ay, Bn)与p (Bn, Ay)的差值, 也就是Ay与Bn的顺序效应, 即量子问题等式左边的部分, 称为第一顺序效应(The First Order Effect); 纵坐标表示p (An, By)与p (By, An)的差值, 即An与By的顺序效应, 为量子问题等式左边部分。图中每个点表示在一个地区进行的实验结果, 图中共有70个点。运用线性拟合的结果显示, 拟合出直线斜率为-1, 相关系数r值为-0.82, 验证了量子问题等式的预测准确性。
图5
图5
量子问题等式统计结果图
(资料来源:Busemeyer & Wang, 2015)
5 总结与展望
近年来, 量子理论在心理学研究领域中的应用已经越来越多。在顺序效应(Wang & Busemeyer, 2013)、因果推理(Trueblood & Busemeyer, 2012)、非对称相似推断(Pothos, Busemeyer, & Trueblood, 2013)以及模糊推断(Blutner et al., 2013)等决策领域中, 都成功的构建了量子模型。除此之外, 在双稳态知觉(Atmanspacher & Filk, 2010)、情景记忆(Brainerd, Wang, & Reyna, 2013), 及联想记忆(Bruza, Kitto, Nelson, & McEvoy, 2009)概念组合(Aerts, Gabora, & Sozzo, 2013)等认知研究领域也都取得了不小的进展。虽然针对不同的研究问题, 所建立量子模型的形式不同, 但尽管表述形式多样, 它们所遵循的公理都相同, 这便是量子模型灵活性与严密性的体现。当然, 作为一个新兴的研究领域, 关于量子理论仍然有许多问题值得进一步探索。这些问题主要有如下几个方面:
第一, 基础理论的探究。量子理论是一个庞大的理论体系, 其中还有许多原理值得量子决策理论借鉴, 例如著名的海森堡的不确定性原理。但最大的挑战在于选取合适的实验方案与测量方式。
第二, 量子理论的生理学基础。量子理论并没有基于人脑是某种量子计算机这一假设, 那么, 为何人在决策过程中会出现一些量子化的行为, 这也是量子理论最使科学家感到疑惑的一个方面, 同时也是最值得深入研究的一个方面。
第三, 不同问题间是否相容的先验性判断方法。在量子决策理论中, 研究者从不同问题间产生的顺序效应引申出了问题间的不相容性, 这是一种后验性分析。因此, 能否在被试做出回答之前对问题之间的相容性做出分析, 是量子决策模型的一个研究趋向, 这将涉及到建构概念空间的量子化模型。
第四, 抽象数学原理在决策领域的应用。传统决策模型, 其数学基础主要为微积分, 概率论和函数论等经典数学理论, 具有具体而明确的特性。而量子决策模型的基础是泛函分析以及抽象代数等更加新颖的现代数学理论, 具有高度抽象与泛化的特性。相比于经典模型, 类似量子模型这样更加抽象与泛化的理论, 在认知与决策领域具有更加广阔的研究与应用前景。
第五, 与现代决策模型相结合。大多数现代决策模型, 可以称之为“定性”的模型, 着重探讨决策形成的心理或外在机制; 量子决策模型, 则是一种“定量”的模型, 着重通过数学建模拟合决策实验结果。因此, 如何将这两类决策模型有机地结合起来, 形成一种既“定性”又“定量”的决策模型, 也是值得探索的一个方向。
第六, 实际问题的应用。目前, 大多数有关量子决策模型的研究重点仍集中于基础理论的探究, 因此, 如何将这种决策模型应用于诸如工程心理学领域中的与决策相关的实际问题中去, 不仅有助于量子决策模型的发展, 而且有着重要的现实意义。
参考文献
概率判断中的合取谬误
DOI:10.3724/SP.J.1042.2015.00967
URL
[本文引用: 1]

概率判断中的合取谬误是指违反事件发生概率的合取规则而认为包含多个独立事件的复合事件的发生可能性大于其中某些事件的发生可能性的一种概率判断偏差现象。合取谬误的界定存在一定争议,相关的解释机制有因果模型理论、确认理论、惊奇理论等,影响合取谬误的因素有频率效应、训练效应以及个体差异等等。未来研究应联系逆转合取谬误的心理机制来完善已有的理论,同时注意应用研究以及其非理性的探讨。
Quantum structure in cognition
DOI:10.1016/j.jmp.2009.04.005 URL [本文引用: 1]
A theory of concepts and their combinations II: A Hilbert space representation
DOI:10.1108/03684920510575807 URL [本文引用: 1]
Concepts and their dynamics: A quantum-theoretic modeling of human thought
DOI:10.1111/tops.12042
URL
PMID:24039114
[本文引用: 1]

We analyze different aspects of our quantum modeling approach of human concepts and, more specifically, focus on the quantum effects of contextuality, interference, entanglement, and emergence, illustrating how each of them makes its appearance in specific situations of the dynamics of human concepts and their combinations. We point out the relation of our approach, which is based on an ontology of a concept as an entity in a state changing under influence of a context, with the main traditional concept theories, that is, prototype theory, exemplar theory, and theory theory. We ponder about the question why quantum theory performs so well in its modeling of human concepts, and we shed light on this question by analyzing the role of complex amplitudes, showing how they allow to describe interference in the statistics of measurement outcomes, while in the traditional theories statistics of outcomes originates in classical probability weights, without the possibility of interference. The relevance of complex numbers, the appearance of entanglement, and the role of Fock space in explaining contextual emergence, all as unique features of the quantum modeling, are explicitly revealed in this article by analyzing human concepts and their dynamics.
New fundamental evidence of non-classical structure in the combination of natural concepts
Kansei versus extensional reasoning: The scientific illusion of the conjunction fallacy in probability judgment
Quantum-like generalization of the Bayesian updating scheme for objective and subjective mental uncertainties
DOI:10.1016/j.jmp.2012.02.003 URL [本文引用: 1]
A proposed test of temporal nonlocality in bistable perception
DOI:10.1016/j.jmp.2009.12.001
URL
[本文引用: 1]

The concept of temporal nonlocality is used to refer to states of a (classical) system that are not sharply localized in time but extend over a time interval of non-zero duration. We investigate the question whether, and how, such a temporal nonlocality can be tested in mental processes. For this purpose we exploit the empirically supported Necker eno model for bistable perception, which uses formal elements of quantum theory but does not refer to anything like quantum physics of the brain. We derive so-called temporal Bell inequalities and demonstrate how they can be violated in this model. We propose an experimental realization of such a violation and discuss some of its consequences for our understanding of mental processes.
Pragmatic approach to decision making under uncertainty: The case of the disjunction effect
DOI:10.1080/13546780500375663
URL
[本文引用: 1]

The disjunction effect (Tversky & Shafir, 1992) occurs when decision makers prefer option x (versus y) when knowing that event A occurs and also when knowing that event A does not occur, but they refuse x (or prefer y) when not knowing whether or not A occurs. This form of incoherence violates Savage's (1954) sure-thing principle, one of the basic axioms of the rational theory of decision making. The phenomenon was attributed to a lack of clear reasons for accepting an option (x) when subjects are under uncertainty. Through a pragmatic analysis of the task and a consequent reformulation of it, we show that the effect does not depend on the presence of uncertainty, but on the introduction of non-relevant goals into the text problem, in both the well-known Gamble problem and the Hawaii problem.
A quantum probability perspective on borderline vagueness
DOI:10.1111/tops.12041
URL
PMID:24039093
[本文引用: 1]

The term 090008vagueness090009 describes a property of natural concepts, which normally have fuzzy boundaries, admit borderline cases, and are susceptible to Zeno's sorites paradox. We will discuss the psychology of vagueness, especially experiments investigating the judgment of borderline cases and contradictions. In the theoretical part, we will propose a probabilistic model that describes the quantitative characteristics of the experimental finding and extends Alxatib's and Pelletier's () theoretical analysis. The model is based on a Hopfield network for predicting truth values. Powerful as this classical perspective is, we show that it falls short of providing an adequate coverage of the relevant empirical results. In the final part, we will argue that a substantial modification of the analysis put forward by Alxatib and Pelletier and its probabilistic pendant is needed. The proposed modification replaces the standard notion of probabilities by quantum probabilities. The crucial phenomenon of borderline contradictions can be explained then as a quantum interference phenomenon.
Superposition of episodic memories: Overdistribution and quantum models
DOI:10.1111/tops.12039
URL
PMID:24027175
[本文引用: 1]

Memory exhibits episodic superposition, an analog of the quantum superposition of physical states: Before a cue for a presented or unpresented item is administered on a memory test, the item has the simultaneous potential to occupy all members of a mutually exclusive set of episodic states, though it occupies only one of those states after the cue is administered. This phenomenon can be modeled with a nonadditive probability model called overdistribution (OD), which implements fuzzy-trace theory's distinction between verbatim and gist representations. We show that it can also be modeled based on quantum probability theory. A quantum episodic memory (QEM) model is developed, which is derived from quantum probability theory but also implements the process conceptions of global matching memory models. OD and QEM have different strengths, and the current challenge is to identify contrasting empirical predictions that can be used to pit them against each other.
Is there something quantum-like about the human mental lexicon?
Quantum cognition: A new theoretical approach to psychology
DOI:10.1016/j.tics.2015.05.001
URL
PMID:26058709
[本文引用: 1]

What type of probability theory best describes the way humans make judgments under uncertainty and decisions under conflict? Although rational models of cognition have become prominent and have achieved much success, they adhere to the laws of classical probability theory despite the fact that human reasoning does not always conform to these laws. For this reason we have seen the recent emergence of models based on an alternative probabilistic framework drawn from quantum theory. These quantum models show promise in addressing cognitive phenomena that have proven recalcitrant to modeling by means of classical probability theory. This review compares and contrasts probabilistic models based on Bayesian or classical versus quantum principles, and highlights the advantages and disadvantages of each approach.
What is quantum cognition, and how is it applied to psychology?
DOI:10.1177/0963721414568663
URL
[本文引用: 4]

Abstract Quantum cognition is a new research program that uses mathematical principles from quantum theory as a framework to explain human cognition, including judgment and decision making, concepts, reasoning, memory, and perception. This research is not concerned with whether the brain is a quantum computer. Instead, it uses quantum theory as a fresh conceptual framework and a coherent set of formal tools for explaining puzzling empirical findings in psychology. In this introduction, we focus on two quantum principles as examples to show why quantum cognition is an appealing new theoretical direction for psychology: complementarity, which suggests that some psychological measures have to be made sequentially and that the context generated by the first measure can influence responses to the next one, producing measurement order effects, and superposition, which suggests that some psychological states cannot be defined with respect to definite values but, instead, that all possible values within the superposition have some potential for being expressed. We present evidence showing how these two principles work together to provide a coherent explanation for many divergent and puzzling phenomena in psychology.
Applying quantum principles to psychology
DOI:10.1088/0031-8949/2014/T163/014007
URL
[本文引用: 1]

This article starts out with a detailed example illustrating the utility of applying quantum probability to psychology. Then it describes several alternative mathematical methods for mapping fundamental quantum concepts (such as state preparation, measurement, state evolution) to fundamental psychological concepts (such as stimulus, response, information processing). For state preparation, we consider both pure states and densities with mixtures. For measurement, we consider projective measurements and positive operator valued measurements. The advantages and disadvantages of each method with respect to applications in psychology are discussed.
Empirical comparison of Markov and quantum models of decision making
DOI:10.1016/j.jmp.2009.03.002
URL
[本文引用: 1]

There are at least two general theories for building probabilistic ynamical systems: one is Markov theory and another is quantum theory. These two mathematical frameworks share many fundamental ideas, but they also differ in some key properties. On the one hand, Markov theory obeys the law of total probability, but quantum theory does not; on the other hand, quantum theory obeys the doubly stochastic law, but Markov theory does not. Therefore, the decision about whether to use a Markov or a quantum system depends on which of these laws are empirically obeyed in an application. This article derives two general methods for testing these theories that are parameter free, and presents a new experimental test. The article concludes with a review of experimental findings from cognitive psychology that evaluate these two properties.
Quantum dynamics of human decision-making
DOI:10.1016/j.jmp.2006.01.003
URL
[本文引用: 2]

A quantum dynamic model of decision-making is presented, and it is compared with a previously established Markov model. Both the quantum and the Markov models are formulated as random walk decision processes, but the probabilistic principles differ between the two approaches. Quantum dynamics describe the evolution of complex valued probability amplitudes over time, whereas Markov models describe the evolution of real valued probabilities over time. Quantum dynamics generate interference effects, which are not possible with Markov models. An interference effect occurs when the probability of the union of two possible paths is smaller than each individual path alone. The choice probabilities and distribution of choice response time for the quantum model are derived, and the predictions are contrasted with the Markov model.
Probabilistic models of cognition: Conceptual foundations
DOI:10.1016/j.tics.2006.05.007
URL
PMID:16807064
[本文引用: 2]

Remarkable progress in the mathematics and computer science of probability has led to a revolution in the scope of probabilistic models. In particular, ‘sophisticated’ probabilistic methods apply to structured relational systems such as graphs and grammars, of immediate relevance to the cognitive sciences. This Special Issue outlines progress in this rapidly developing field, which provides a potentially unifying perspective across a wide range of domains and levels of explanation. Here, we introduce the historical and conceptual foundations of the approach, explore how the approach relates to studies of explicit probabilistic reasoning, and give a brief overview of the field as it stands today.
Quantum mechanics, interference, and the brain
DOI:10.1016/j.jmp.2009.03.005
URL

In this paper we discuss the use of quantum mechanics to model psychological experiments, starting by sharply contrasting the need of these models to use quantum mechanical nonlocality instead of contextuality. We argue that contextuality, in the form of quantum interference, is the only relevant quantum feature used. Nonlocality does not play a role in those models. Since contextuality is also present in classical models, we propose that classical systems be used to reproduce the quantum models used. We also discuss how classical interference in the brain may lead to contextual processes, and what neural mechanisms may account for it.
Commentary: Extensional versus intuitive reasoning: The conjunction fallacy in probability judgment
A test of “reason-based” and “reluctance-to-think” accounts of the disjunction effect
DOI:10.1016/j.ins.2011.09.002
URL
[本文引用: 1]

The disjunction effect violates Savage’s sure-thing principle: that is, if is preferred over regardless of whether relevant outcome occurs, then should always be preferred over [L.J. Savage, The Foundations of Statistics, New York, Wiley, 1954]. We tested “reason-based” and “reluctance-to-think” accounts of the disjunction effect. According to the former account, the disjunction effect occurs when different reasons underlie the preference for under versus the preference for under not . According to the latter account, the disjunction effect is due to the failure to consider preferences when is unknown. We tested these accounts by varying the number of reasons underlying choices in the and not conditions. Consistent with the reason-based account, when only one reason was available, the disjunction effect was reduced. In addition, we propose a new method of measuring the disjunction effect under different conditions based on the logic proposed by Lambdin and Burdsal (2007) [C. Lambdin, C. Burdsal, The disjunction effect reexamined: relevant methodological issues and the fallacy of unspecified percentage comparisons, Organizational Behavior and Human Decision Processes 103 (2007) 268–276].
Examining whether there is a disjunction effect in prisoner's dilemma games
react-text: 480 We investigate the eigenvalue curves, the behavior of the periodic solutions, and the orthogonality properties of the Mathieu equation with an additional fractional derivative term using the method of harmonic balance. The addition of the fractional derivative term breaks the hermiticity of the equation in such a way that its eigenvalues need not be real nor its eigenfunctions orthogonal. We... /react-text react-text: 481 /react-text [Show full abstract]
Measuring new types of question-order effects: Additive and subtractive
DOI:10.1086/338631 URL [本文引用: 1]
A quantum probability explanation for violations of 'rational' decision theory
DOI:10.1098/rspb.2009.0121
URL
PMID:19324743
[本文引用: 2]

Abstract Two experimental tasks in psychology, the two-stage gambling game and the Prisoner's Dilemma game, show that people violate the sure thing principle of decision theory. These paradoxical findings have resisted explanation by classical decision theory for over a decade. A quantum probability model, based on a Hilbert space representation and Schr dinger's equation, provides a simple and elegant explanation for this behaviour. The quantum model is compared with an equivalent Markov model and it is shown that the latter is unable to account for violations of the sure thing principle. Accordingly, it is argued that quantum probability provides a better framework for modelling human decision-making.
A quantum geometric model of similarity
DOI:10.1037/a0033142
URL
PMID:23915087
[本文引用: 1]

No other study has had as great an impact on the development of the similarity literature as that of Tversky (1977), which provided compelling demonstrations against all the fundamental assumptions of the popular, and extensively employed, geometric similarity models. Notably, similarity judgments were shown to violate symmetry and the triangle inequality and also be subject to context effects, so that the same pair of items would be rated differently, depending on the presence of other items. Quantum theory provides a generalized geometric approach to similarity and can address several of Tversky's main findings. Similarity is modeled as quantum probability, so that asymmetries emerge as order effects, and the triangle equality violations and the diagnosticity effect can be related to the context-dependent properties of quantum probability. We so demonstrate the promise of the quantum approach for similarity and discuss the implications for representation theory in general.
Reexamining the role of the description of problem texts in the disjunction effect
DOI:10.3200/JRLP.142.3.261-266
URL
PMID:18589936
[本文引用: 1]

M. Bagassi and L. Macchi (2006) demonstrated that through a pragmatic analysis and consequent reformulation of a task, the certainty vs. uncertainty condition is not a crucial factor to the disjunction effect. In addition, C. Lambdin and C. Burdsal (2007) argued that, given the defining characteristics of a disjunction effect, a between-subjects design does not allow for the conditions necessary for a disjunction effect to occur. In the present study, the authors reexamined the role of text's description in the disjunction effect using a within-subject experimental design rather than a between-subjects design across 3 conditions. The results support M. Bagassi and L. Macchi's conclusion, regardless of whether the information presentation was transparent or not.
Theory-based Bayesian models of inductive learning and reasoning
DOI:10.1016/j.tics.2006.05.009
URL
PMID:16797219
[本文引用: 2]

Abstract Inductive inference allows humans to make powerful generalizations from sparse data when learning about word meanings, unobserved properties, causal relationships, and many other aspects of the world. Traditional accounts of induction emphasize either the power of statistical learning, or the importance of strong constraints from structured domain knowledge, intuitive theories or schemas. We argue that both components are necessary to explain the nature, use and acquisition of human knowledge, and we introduce a theory-based Bayesian framework for modeling inductive learning and reasoning as statistical inferences over structured knowledge representations.
Exploring the relations between categorization and decision making with regard to realistic face stimuli
A quantum probability model of causal reasoning
DOI:10.3389/fpsyg.2012.00138
URL
PMID:3350941
[本文引用: 1]

People can often outperform statistical methods and machine learning algorithms in situations that involve making inferences about the relationship between causes and effects. While people are remarkably good at causal reasoning in many situations, there are several instances where they deviate from expected responses. This paper examines three situations where judgments related to causal inference problems produce unexpected results and describes a quantum inference model based on the axiomatic principles of quantum probability theory that can explain these effects. Two of the three phenomena arise from the comparison of predictive judgments (i.e., the conditional probability of an effect given a cause) with diagnostic judgments (i.e., the conditional probability of a cause given an effect). The third phenomenon is a new finding examining order effects in predictive causal judgments. The quantum inference model uses the notion of incompatibility among different causes to account for all three phenomena. Psychologically, the model assumes that individuals adopt different points of view when thinking about different causes. The model provides good fits to the data and offers a coherent account for all three causal reasoning effects thus proving to be a viable new candidate for modeling human judgment.
Judgment under uncertainty: Heuristics and biases
DOI:10.1126/science.185.4157.1124
URL
PMID:17835457
[本文引用: 3]

This article described three heuristics that are employed in making judgements under uncertainty: (i) representativeness, which is usually employed when people are asked to judge the probability that an object or event A belongs to class or process B; (ii) availability of instances or scenarios, which is often employed when people are asked to assess the frequency of a class or the plausibility of a particular development; and (iii) adjustment from an anchor, which is usually employed in numerical prediction when a relevant value is available. These heuristics are highly economical and usually effective, but they lead to systematic and predictable errors. A better understanding of these heuristics and of the biases to which they lead could improve judgements and decisions in situations of uncertainty.
The disjunction effect in choice under uncertainty
DOI:10.1111/j.1467-9280.1992.tb00678.x
URL
[本文引用: 2]

Abstract One of the basic axioms of the rational theory of decision under uncertainty IS Savage's (1954) sure-thing principle (STP) It states that if prospect x is preferred to y knowing that Event A occurred, and if x IS preferred to y knowing that A did not occur, then x should be preferred to y even when it is not known whether A occurred We present examples in which the decision maker has good reasons for accepting x if A occurs, and different reasons for accepting X if A does not occur Not knowing whether or not A occurs, however, the decision maker may lack a clear reason for accepting X and may opt for another option We suggest that, in the presence of uncertainty, people are often reluctant to think through the implications of each outcome and, as a result, may violate STP This interpretation is supported by the observation that STP is satisfied when people are made aware of their preferences given each outcome
A quantum question order model supported by empirical tests of an A priori and precise prediction
Interference effects of categorization on decision making
DOI:10.1016/j.cognition.2016.01.019
URL
PMID:26896726
[本文引用: 1]

Many decision making tasks in life involve a categorization process, but the effects of categorization on subsequent decision making has rarely been studied. This issue was explored in three experiments ( N = 721), in which participants were shown a face stimulus on each trial and performed variations of categorization-decision tasks. On C-D trials, they categorized the stimulus and then made an action decision; on X-D trials, they were told the category and then made an action decision; on D-alone trials, they only made an action decision. An interference effect emerged in some of the conditions, such that the probability of an action on the D-alone trials (i.e., when there was no explicit categorization before the decision) differed from the total probability of the same action on the C-D or X-D trials (i.e., when there was explicit categorization before the decision). Interference effects are important because they indicate a violation of the classical law of total probability, which is assumed by many cognitive models. Across all three experiments, a complex pattern of interference effects systematically occurred for different types of stimuli and for different types of categorization-decision tasks. These interference effects present a challenge for traditional cognitive models, such as Markov and signal detection models, but a quantum cognition model, called the belief-action entanglement (BAE) model, predicted that these results could occur. The BAE model employs the quantum principles of superposition and entanglement to explain the psychological mechanisms underlying the puzzling interference effects. The model can be applied to many important and practical categorization-decision situations in life.
Emotional response in a disjunction condition
Quantum cognition and decision theories: A tutorial
DOI:10.1016/j.jmp.2015.11.005
URL

The purpose of this tutorial is to give an introduction to quantum models, with a particular emphasis on how to build these models in practice. Examples are provided by the study of order effects on judgements, and we will show how order effects arise from the structure of the theory. In particular, we show how to derive the recent discovery of a particular constraint on order effects implied by quantum models, called the Quantum Question (QQ) Equality, which does not appear to be derivable from alternative accounts, and which has been experimentally verified to high precision. However the general theory and methods of model construction we will describe are applicable to any quantum cognitive model. Our hope is that this tutorial will give researchers the confidence to construct simple quantum models of their own, particularly with a view to testing these against existing cognitive theories.